
- •4. Преобразование Фурье
- •Преобразование Фурье
- •Преобразование Фурье
- •4.1.Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •Ряд Фурье
- •4.2.Временная и частотные области
- •Временная и частотные области сигнала
- •Временная и частотные области сигнала
- •Временная и частотные области сигнала
- •Spectral Plot
- •4.3.Комплексная форма ряда Фурье
- •4.3.Комплексная форма ряда Фурье
- •4.3.Комплексная форма ряда Фурье
- •4.4.Интеграл Фурье
- •4.4.Интеграл Фурье
- •4.4. Интеграл Фурье
- •4.4. Интеграл Фурье
- •4.4.Интеграл Фурье
- •4.5.Преобразование Фурье
- •4.5. Преобразование Фурье
- •4.5.Преобразование Фурье
- •4.5.Преобразование Фурье
- •4.5.Преобразование Фурье
- •4.5. Преобразование Фурье
- •4.6.Синус- и косинус-
- •4.6.Синус- и косинус-
- •4.6.Синус- и косинус-
- •4.6.Синус- и косинус-
- •4.6. Синус- и косинус-
- •4.7.Фурье-образ δ-функции
- •4.7.Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.7. Фурье-образ δ-функции
- •4.8.Свойства преобразования Фурье
- •4.8.Свойства преобразования Фурье
- •4.9. Преобразование Фурье
- •4.9. Преобразование Фурье триг.
- •4.9. Преобр Фурье триг. функций–
- •4.9. Преобразование Фурье триг.
- •4.9. Преобразование Фурье триг.
- •4.10. Преобразование Фурье для свертки
- •4.10. Преобразование Фурье для свертки
- •4.10.Преобразование Фурье для свертки
- •4.11.Оконные функции
- •4.11.Оконные функции
- •4.11.Оконные функции
- •4.11. Оконные функции
- •4.11. Оконные функции
- •4.11.Оконные функции
- •4.11.Оконные функции
- •4.11.Оконные функции
- •Example 2.3.14 (2/2) Пример слайда по этой теме из
- •4.12.Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12. Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12. Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.12. Равенство Парсеваля
- •4.12.Равенство Парсеваля
- •4.13.Применение равенства Парсеваля
- •4.13.Применение равенства Парсеваля
- •4.13.Применение равенства Парсеваля
- •4.13.Применение равенства Парсеваля
- •4.14. Энергия гармонического
- •4.14.Энергия гармонического
- •4.14.Энергия гармонического
- •4.14.Энергия гармонического
- •4.14. Энергия гармонического
- •4.14.Энергия гармонического
- •4.15.Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15.Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье
- •4.15. Приложения преобразования Фурье

4.15.Приложения преобразования Фурье
Ряды Фурье и преобразование Фурье были созданы для изучения распространения тепла в твердых и жидких средах. Фурье всю жизнь исследовал тепловые процессы. Один из опытов был посвящен распространению тепла по якорному кольцу (железному кольцу, к которому крепится якорь), погружаемому на некоторое время наполовину в раскаленные угли. Когда часть кольца раскаляется докрасна, его вынимают из огня. Чтобы тепло не успело уйти в воздух, кольцо сразу закапывают в мелкий песок, а затем измеряют температуру на той его части, которая огнём не нагревалась.
Page 92

4.15.Приложения преобразования Фурье
График изменения температуры плавно нарастает (в холодной части) и убывает (в раскаленной части) в виде функции синуса (или косинуса). Синусоида постепенно выравнивается и в конце концов температура по всему кольцу становится одинаковой. Фурье нашел, что первоначальное нерегулярное распределение можно разложить на множество простых синусоид, каждая из которых имеет свой максимум температуры и свою фазу, т.е. начальное положение на кольце. При этом каждая синусоидальная компонента должна изменяться от максимума к минимуму и обратно целое число раз на одном полном обороте по кольцу.
Page 93

4.15.Приложения преобразования Фурье
Составляющая, которая имеет ровно один период на кольце (время, за которое тепло проходит полный круг, неизвестно, оно бралось достаточно произвольно), была названа главной гармоникой, а составляющие с двумя, тремя и более периодами
—соответственно второй, третьей и т.д. гармоникой. Так был построен ряд Фурье.
Фурье свёл функцию распределения тепла, трудно поддающуюся математическому описанию, к удобным для анализа суммам синусов и косинусов, эти суммы очень точно описывали распределение тепла.
Page 94
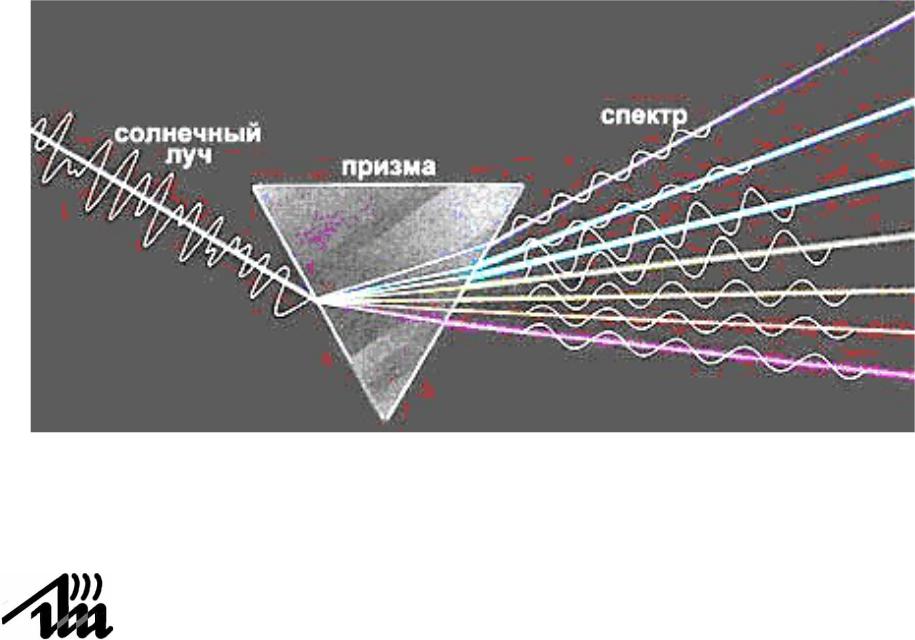
4.15. Приложения преобразования Фурье
Page 95

4.15.Приложения преобразования Фурье
В конце XIX века лорд Кельвин применил ряды Фурье как основу аналогового вычислительного устройства, которое позволяло морякам оценивать высоту приливов и отливов. Аналоговый вычислитель механически определял наборы амплитуд и фаз по наблюдениям приливных высот в зависимости от времени. Высоты замерялись на протяжении года в данной гавани.
Каждая амплитуда и фаза представляли синусоидальную компоненту функции высоты прилива
ибыли одной из периодических составляющих. Результаты вводились в вычислительное устройство лорда Кельвина, которое синтезировало кривую, предсказывающую высоту прилива как функцию времени на следующий год. Метод оказался настолько успешным, что такие кривые приливов были составлены для всех портов мира.
Page 96

4.15.Приложения преобразования Фурье
Преобразованием Фурье можно фильтровать фотографии, спутниковые снимки, рентгеновские, магнитно-ядерные, ультразвуковые сканирования органов тела.
Можно изучать вибрацию машин и механизмов, явление флаттера технических сооружений.
Page 97
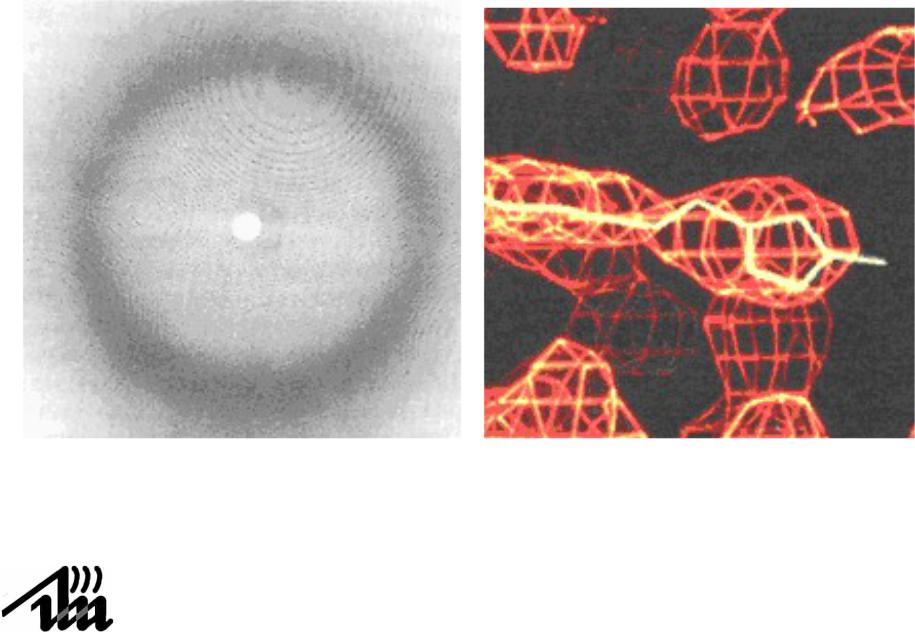
4.15. Приложения преобразования Фурье
Рентгеновский снимок (слева) близок к Фурье- образу колонии вирусов.
Page 98
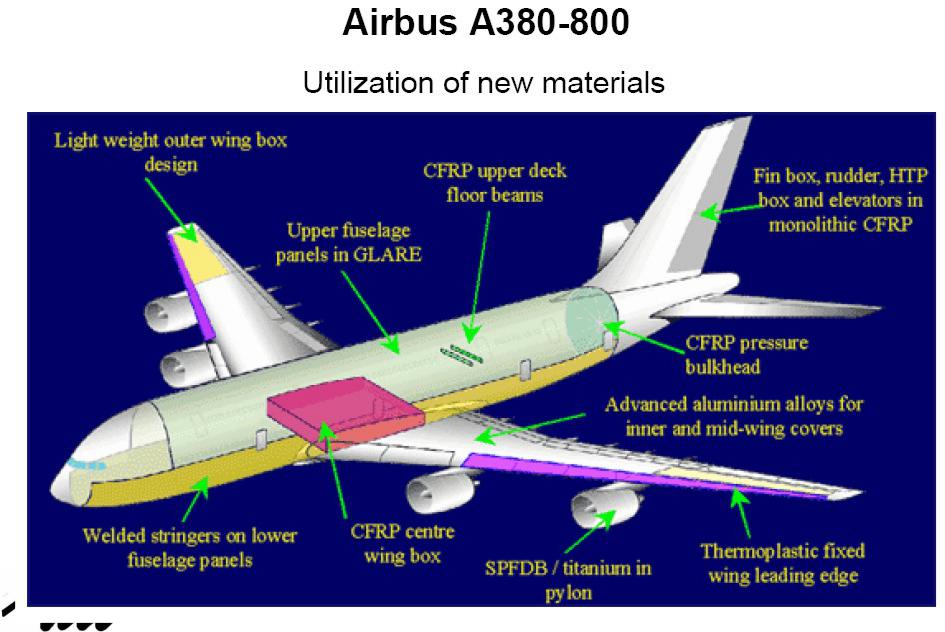
4.15. Приложения преобразования Фурье
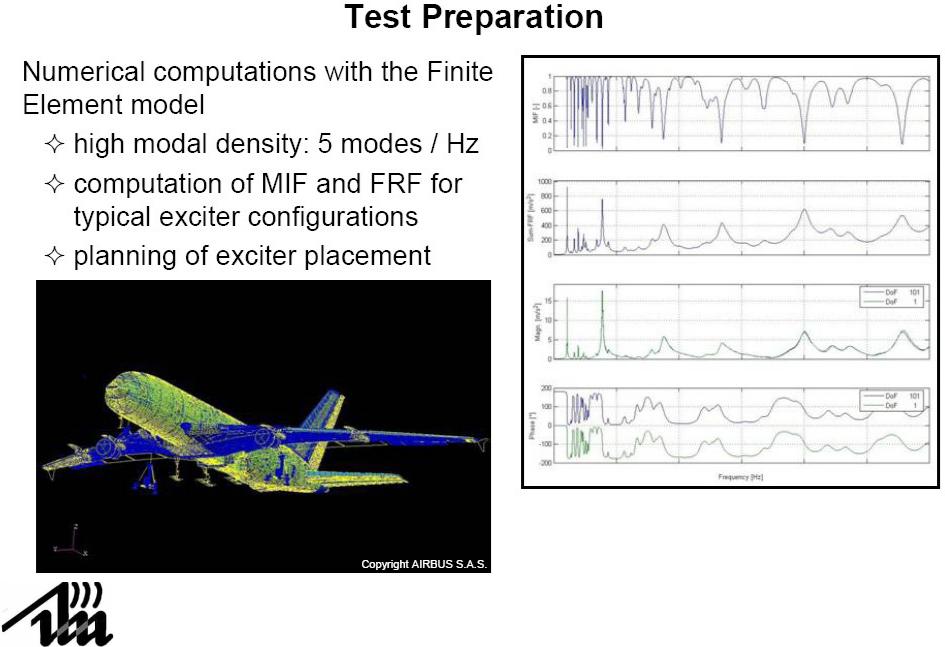
4.15. Приложения преобразования Фурье
Page 100

4.15. Приложения преобразования Фурье
Page 101
