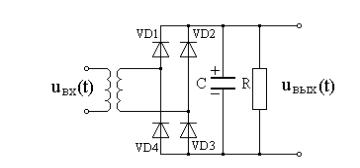
в. Мостовая схема двухполупериодного выпрямителя
Эти недостатки отсутствуют в мостовой схеме двухполупериодного выпрямителя. В этом выпрямителе (рис 8.19) вторичная обмотка не имеет средней точки и используется полностью в течение положительного и отрицательного полупериода напряжения. В положительный полупериод открыты диоды VD1 и VD3 (диоды VD2 и VD4 закрыты), в отрицательный полупериод открыты диоды VD2 и VD4 (диоды VD1 и VD3 закрыты). Через открытые диоды происходит заряд конденсатора фильтра.
Рис. 8.19. Схема мостового двухполупериодного выпрямителя
Мостовая схема выпрямителя имеет два важных преимущества. Во-первых, обратное напряжение на диодах в 2 раза меньше, чем у других выпрямителей. Во-вторых, можно применить более простой трансформатор (без средней точки), который может и отсутствовать. В силу того что ток заряда конденсатора проходит через два диода, у этого выпрямителя потери несколько больше.
Применяются также схемы выпрямителей с определенными специфическими свойствами, например, с удвоением или умножением выходного напряжения. Такие выпрямители позволяют получить выходное напряжение значительно большее, чем амплитуда входного переменного напряжения (до нескольких десятков киловольт).
8.6.Угловая модуляция
8.6.1.Общие принципы получения сигналов с угловой модуляцией
Радиосигналы с угловой модуляцией имеют вид s(t) Uн cos[ 0t (t)],
где (t) kфsм(t) 0 – изменение фазы несущего колебания при фазовой мо-
дуляции;
t
(t) kч sм(t)dt 0 – изменение фазы несущего колебания при частот-
0
ной модуляции.
Здесь sм(t) – модулирующий сигнал, 0 – начальная фаза несущего колебания , kф и kч – масштабные коэффициенты.
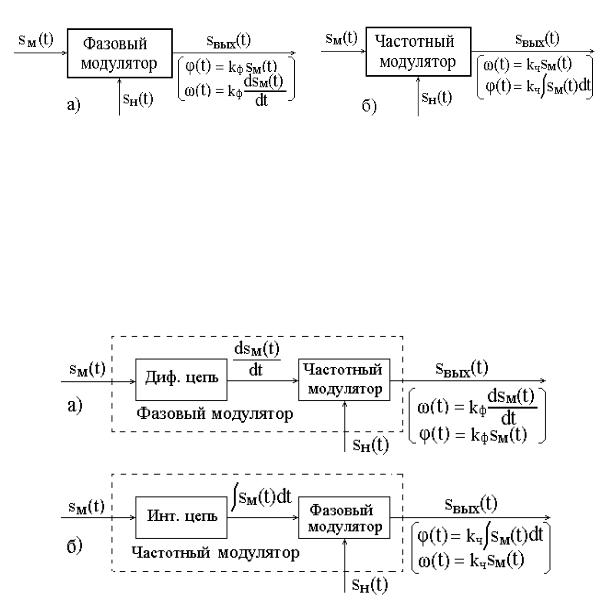
Такие радиосигналы формируются фазовыми и частотными модуляторами. Фазовый модулятор (ФМ) – это устройство, формирующее высокочастотное колебание, фаза которого изменяется по закону модулирующего сигнала
(рис. 8.20,а).
Частотный модулятор (ЧМ) – это устройство, формирующее высокочастотное колебание, частота которого изменяется по закону модулирующего сиг-
нала (рис. 8.20,б).
Рис. 8.20. Фазовый (а) и частотный (б) модуляторы
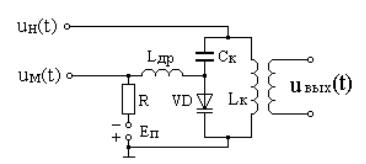
Фазомодулированное колебание можно получить и с помощью частотного модулятора. Для этого необходимо модулирующий сигнал подать на модулятор через дифференцирующую цепь (диф. цепь, рис. 8.21,а). В свою очередь с помощью фазового модулятора можно получить частотно-модулированное колебание, если модулирующий сигнал подается на модулятор через интегрирующую цепь (инт. цепь, рис. 8.21,б).
Рис. 8.21. Взаимосвязь частотной и фазовой модуляций
8.6.2. Фазовые модуляторы
Изменение фазы несущего колебания по закону модулирующего сигнала наиболее просто осуществляется с помощью колебательного контура с пере-
страиваемой фазочастотной характеристикой. Управляя этой характеристикой с помощью модулирующего сигнала, можно изменять в определенных пределах фазу высокочастотного колебания, поступающего на контур. ФЧХ контура зависит от его параметров (индуктивности, емкости, сопротивления). Поэтому управление этой характеристикой можно осуществить, изменяя, например, величину емкости контура с помощью варикапа – параметрического плоскостного диода, барьерная емкость p-n-перехода которого зависит от обратного напряжения, приложенного к нему. Для осуществления процедуры модуляции на варикап необходимо подать модулирующий сигнал.
Схема такого фазового модулятора представлена на рис. 8.22.
Рис. 8.22. Фазовый модулятор на основе перестраиваемого контура
Для устранения паразитной амплитудной модуляции, вызванной неизбежной расстройкой контура относительно частоты несущего колебания, к выходу модулятора подключается усилитель-ограничитель.
Фаза выходного сигнала вых модулятора будет определяться изменением фазового сдвига контура к по закону модулирующего сигнала uм(t), т.е.
вых[uм(t)] к[uм(t)] 0.
Индекс угловой модуляции определяется произведением амплитуды модулирующего сигнала Uм на крутизну модуляционной характеристики, равную Sф d к (u)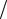
du. Крутизна модуляционной характеристики зависит от доброт-
ности контура, порядка включения варикапа в контур (последовательно или параллельно емкости контура) и крутизны вольт-кулонной характеристики варикапа. При необходимости получить значительный индекс угловой модуляции применяется умножитель частоты выходного сигнала.
Другой способ построения фазовых модуляторов основан на преобразовании амплитудной модуляции в фазовую. В таких модуляторах формирование ФМ-сигнала производится в два этапа. На первом этапе формируется АМсигнал, а на втором этапе осуществляется преобразование данного сигнала в сигнал с фазовой модуляцией.
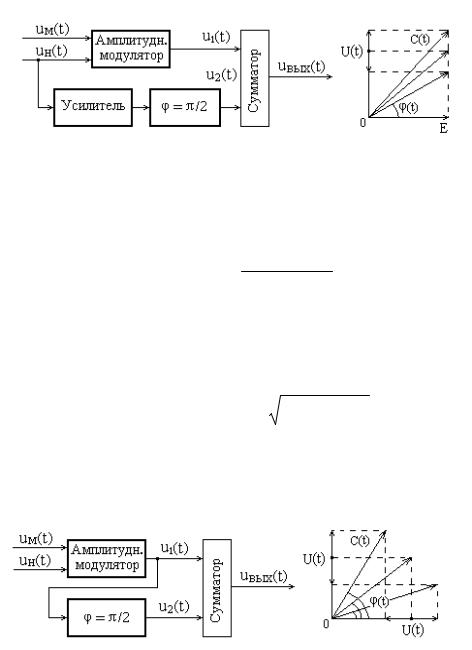
Второй этап выполняется путем сложения двух колебаний несущей частоты, сдвинутых относительно друг друга на угол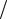 
2. Причем амплитудномодулированными могут быть одно или оба складываемых колебаний.
На рис. 8.23 и 8.24 приведены схемы подобных фазовых модуляторов и векторные диаграммы, поясняющие эффект фазовой модуляции.
Рис. 8.23. Фазовый модулятор
Фазовый модулятор рис. 8.23 реализует свои функции путем сложения ам- плитудно-модулированного u1(t) U(t)cos 0t и немодулированного u2(t) Esin 0t колебаний. Выходной сигнал равен
uвых(t) U(t)cos 0t Esin 0t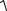 
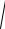U 2(t) E2 sin{ 0t arctg[U(t)
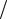E]}.
Как видно из этого выражения, выходной сигнал представляет собой высокочастотное гармоническое колебание, амплитуда и фаза которого зависит от модулирующего колебания. Векторная диаграмма иллюстрирует эффект изменения фазы и тот факт, что фазовая модуляция в этом случае сопровождается
паразитным изменением амплитуды C(t) |
U2(t) E2 результирующего сиг- |
нала.
При сложении двух амплитудно-модулированных колебаний (рис. 8.24) можно значительно уменьшить изменения амплитуды фазомодулированного сигнала.
Рис. 8.24. Фазовый модулятор
При небольших индексах угловой модуляции (не более 0,5) для получения сигналов с фазовой модуляцией можно использовать метод Армстронга (Эдвин Армстронг – американский радиотехник). Метод предусматривает сложение под углом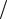 
2 немодулированного и балансно-модулированного колебаний. Схема фазовой модуляции по методу Армстронга и векторная диаграмма, поясняющая эффект модуляции, приведены на рис. 8.25. Диаграмма приведена для однотональной фазовой модуляции.