Умножение частоты можно осуществить также с помощью параметрических цепей (например цепей с варактором). В рамках данного учебного пособия эта проблема не рассматривается.

8.3.Амплитудная модуляция

8.3.1.Общие сведения об амплитудной модуляции

Амплитудная модуляция – это процесс формирования амплитудно-моду- лированного сигнала, т.е. сигнала, амплитуда которого изменяется по закону модулирующего сигнала (передаваемого сообщения). Этот процесс реализуется амплитудным модулятором.

Амплитудный модулятор должен формировать высокочастотное колебание, аналитическое выражение для которого в общем случае имеет вид

где U(t) – огибающая модулированного колебания, описываемая функцией, которая характеризует закон изменения амплитуды;

sм(t) – модулирующий сигнал;

0 и – частота и начальная фаза высокочастотного колебания.

Для получения такого сигнала необходимо осуществить перемножение высокочастотного (несущего) колебания sн(t) Uн cos( 0t ) и низкочастотного модулирующего сигнала sм (t) таким образом, чтобы сформировалась огибающая вида U(t) Uн kasм(t). Наличие постоянной составляющей в структуре огибающей обеспечивает однополярность ее изменения, коэффициент ka исключает перемодуляцию, т.е. обеспечивает глубину модуляции m 1. Понятно, что такая операция перемножения будет сопровождаться трансформацией спектра, что позволяет рассматривать амплитудную модуляцию как существенно нелинейный или параметрический процесс.

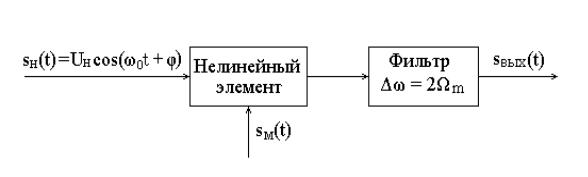
Структура амплитудного модулятора в случае использования нелинейного элемента представлена на рис. 8.4.

Рис. 8.4. Структурная схема амплитудного модулятора

Нелинейный элемент осуществляет преобразование несущего колебания и модулирующего сигнала, в результате чего формируется ток (или напряжение),

вспектре которого содержатся составляющие в полосе частот от 0 m до

0 m, причем m – наивысшая частота в спектре модулирующего сигнала.

Полосовой фильтр выделяет эти составляющие спектра, формируя амплитудномодулированный сигнал на выходе.

Перемножение двух сигналов можно осуществить с помощью нелинейного элемента, характеристика которого аппроксимируется полиномом, содержащим квадратичный член. Благодаря этому формируется квадрат суммы двух сигналов, содержащий их произведение.

Суть сказанного и общую идею формирования амплитудно-модулирован- ного колебания иллюстрируют достаточно простые математические преобразования в предположении, что осуществляется тональная (одной частотой) модуляция.

1.В качестве нелинейного элемента используем транзистор, ВАХ которого аппроксимируется полиномом второй степени i a0 a1u a2u2.

2.На вход нелинейного элемента подается напряжение, равное сумме двух колебаний: несущего и модулирующего, т.е.

u(t) Uн cos( 0t ) Uм cos( t ).

Начальные фазы колебаний будем считать в дальнейшем равными 0, т.к. их величины не имеют принципиального значения для понимания процесса амплитудной модуляции.

3. Спектральный состав тока определяется следующим образом: i(t) a0 a1(Uн cos 0t Uм cos t) a2(Uн cos 0t Uм cos t)2

a1Uн cos 0t a2UнUм cos( 0 )t a2Uн2 cos2 0t . 2

В полученном выражении спектральные составляющие расположены в порядке возрастания их частот. Среди них имеются составляющие с частотами0 , 0 и 0 , которые образуют амплитудно-модулированное колебание, т.е.

iам (t) a2UнUм cos( 0 )t a1Uн cos 0t a2UнUм cos( 0 )t

В передающих устройствах обычно совмещают процессы модуляции и усиления, что обеспечивает минимальные искажения модулированных сигна-

лов. С этой целью амплитудные модуляторы строят по схеме резонансных усилителей мощности, в которых изменение амплитуды высокочастотных колебаний достигается изменением положения рабочей точки по закону модулирующего сигнала.

8.3.2. Схема и режимы работы амплитудного модулятора

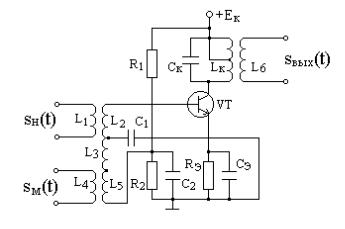
Схема амплитудного модулятора на основе резонансного усилителя представлена на рис. 8.5.

Рис. 8.5. Схема амплитудного модулятора на основе резонансного усилителя

На вход резонансного усилителя, работающего в нелинейном режиме, подаются:

несущее колебание sн(t) от автогенератора с помощью высокочастотной трансформаторной связи контура входной цепи с базой транзистора;

модулирующий сигнал sм(t) с помощью низкочастотного трансформато-

ра.

Конденсаторы C1 и C2 – блокировочные, обеспечивают развязку входных цепей по частотам несущего колебания и модулирующего сигнала, т.е. развязку по высокой и низкой частотам. Колебательный контур в цепи коллектора настроен на частоту несущего колебания, добротность контура обеспечивает полосу пропускания 2 m , где m – наивысшая частота в спектре модулирующего сигнала.

Выбором рабочей точки определяется режим работы модулятора. Возможны два режима: режим малых и режим больших сигналов.

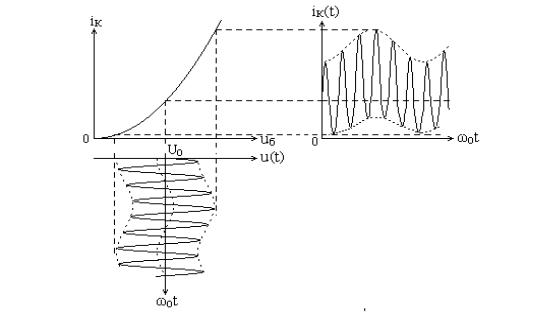
а. Режим малых входных сигналов

Этот режим устанавливается выбором рабочей точки в середине квадратичного участка ВАХ транзистора. Выбором амплитуды несущего колебания обеспечивается работа модулятора в пределах этого участка (рис. 8.6).

Рис. 8.6. Режим малых входных сигналов амплитудного модулятора

Амплитуда напряжения на колебательном контуре, резонансная частота которого равна несущей частоте, определяется амплитудой первой гармоники тока, т.е. Uk I1R0 , где R0 – резонансное сопротивление контура. Учитывая, что средняя крутизна ВАХ в пределах рабочего участка равна отношению амплитуды первой гармоники к амплитуде несущего колебания, т.е. Sср I1Uн ,

можно записать

Uk UнR0Sср.

Под воздействием модулирующего напряжения, подаваемого на базу транзистора, будет изменяться положение рабочей точки, а значит, будет изменяться и средняя крутизна ВАХ. Так как амплитуда напряжения на колебательном контуре пропорциональна средней крутизне, то для обеспечения амплитудной модуляции несущего колебания необходимо обеспечить линейную зависимость крутизны от модулирующего сигнала. Покажем, что это возможно при использовании рабочего участка ВАХ, аппроксимируемого полиномом второй степени.

Итак, в пределах квадратичного участка ВАХ, описываемого полиномом i a0 a1u a2u2 , существует входное напряжение, равное сумме двух колебаний: несущего и модулирующего, т.е.

u(t) Uн cos( 0t ) Uм cos( t ).

Начальные фазы колебаний будем считать в дальнейшем равными 0, т.к. их величины не имеют принципиального значения для понимания процесса амплитудной модуляции. Спектральный состав тока коллектора определяется следующим образом:

i(t) a0 a1(Uн cos 0t Uм cos t) a2(Uн cos 0t Uм cos t)2a0 a1Uнcos 0t a1Uмcos t a2(Uн2 cos2 0t Uм2 cos2 t

2UнU м cos 0tcos t).

Выделяем первую гармонику тока

i1(t) a1Uн cos 0t 2a2UнUм cos tcos 0t Uн (a1 2a2U м cos t)cos 0t .

Таким образом, амплитуда первой гармоники равна

I1(t) Uн (a1 2a2Uм cos t) .

Как видно из полученного выражения, амплитуда первой гармоники тока линейно зависит от модулирующего напряжения. Следовательно, средняя крутизна также будет линейно зависеть от модулирующего напряжения.

Sср(t) I1(t)Uн a1 2a2Uм cos t.

Тогда напряжение на колебательном контуре будет равно

Uk(t) UнR0Sср(t)cos 0t UнR0(a1 2a2Uм cos t)cos 0t.

Следовательно, на выходе рассматриваемого модулятора формируется ампли- тудно-модулированный сигнал вида:

sвых(t) a1UнR0(1 2Uм a2 cos t)cos 0t Uнв(1 mcos t)cos 0t. a1

Здесь m 2Uм a2 – коэффициент глубины модуляции; a1

Uнв a1UнR0 – амплитуда высокочастотного колебания на выходе модулятора в отсутствие модуляции, т.е. при m 0.

При проектировании передающих систем важным требованием является формирование амплитудно-модулированных колебаний большой мощности при достаточном КПД. Очевидно, что рассмотренный режим работы модулятора не может обеспечить эти требования, особенно первое из них. Поэтому наиболее часто используют так называемый режим больших сигналов.

б. Режим больших входных сигналов

Этот режим устанавливается выбором рабочей точки на ВАХ транзистора, при котором усилитель работает с отсечкой тока. В свою очередь выбором амплитуды несущего колебания обеспечивается изменение амплитуды импульсов тока коллектора Im(t) по закону модулирующего сигнала (рис. 8.7). Это приводит к аналогичному изменению амплитуды первой гармоники коллекторного тока и, следовательно, изменению амплитуды напряжения на колебательном контуре модулятора, так как