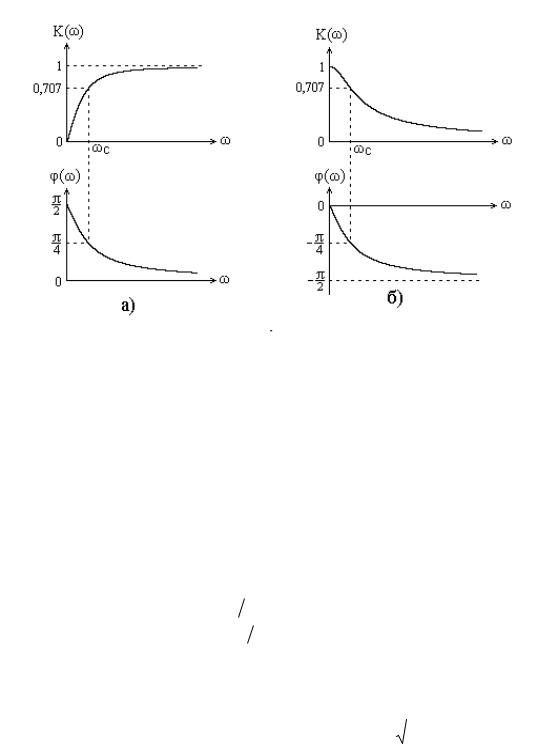
Рис. 5.2. АЧХ и ФЧХ дифференцирующей (а) и интегрирующей (б) цепей
5.4.Фильтр нижних частот
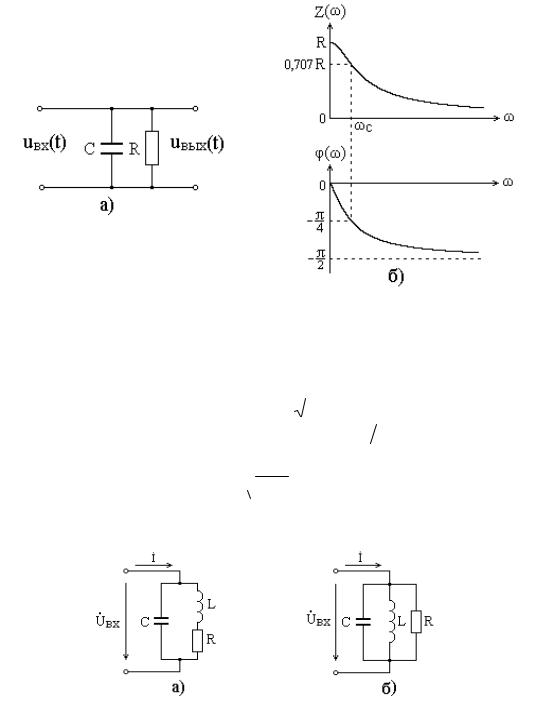
Вкачестве фильтра нижних частот во многих радиотехнических устройствах (выпрямителях, детекторах и др.) применяется схема, изображенная на рис. 5.3,а.
Частотно-избирательные свойства этого фильтра характеризует комплексное входное сопротивление Z( j ). Оно равно отношению комплексной ампли-
туды выходного напряжения к комплексной амплитуде тока в цепи и определяется следующим выражением:
Z(j ) |
Uвых |
|
R(1 |
j C) |
|
R |
|
|
|
R |
, |
(5.4) |
||
I |
|
|
1 j RC |
|
|
|||||||||
|
|
R 1 j C |
|
|
1 j |
|
|
|||||||
где RC – постоянная времени фильтра. |
|
|
|
|
|
|
|
|
|
|||||
Отсюда: |
|
|
|
|
|
|
|
|
|
R |
|
|
||
амплитудно-частотная характеристика |
Z( ) |
|
|
|
|
; |
||||||||
|
|
|
|
|
|
|||||||||
|
|
1 2 2 |
||||||||||||
фазочастотная характеристика |
( ) arctg . |
|
|
|||||||||||
|
|
|
|
|
||||||||||
Графики АЧХ и ФЧХ приведены на рис. 5.3,б.
Как следует из графика АЧХ, рассматриваемый фильтр является фильтром нижних частот. Частота среза равна 1
.
5.5. Параллельный колебательный контур
Параллельный колебательный контур – это частотно-избирательная цепь, образованная параллельным соединением индуктивности L и емкости C. Активные потери контура учитываются сопротивлением R, которое подключается последовательно или параллельно (рис. 5.4а,б). Контур широко используется как самостоятельно (полосовой фильтр), так и в составе различных радиотехнических устройств (автогенераторов, модуляторов, преобразователей частоты и др.).
Рис. 5.3. Фильтр нижних частот (а), АЧХ и ФЧХ фильтра (б)
Основные параметры контура и их математические выражения [4,7]:
1. |
Резонансная частота контура p |
|
|
1 |
|
. |
|
|
|
|
|||
|
|
|||||
|
|
|
|
LC |
||
2. |
Добротность контура (рис. 5.4,а) |
Q R, добротность контура |
||||
(рис. 5.4,б) Q R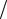
.
3.Волновое сопротивление 
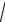L
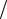C 1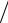
pC pL.
4.Затухание контура d 1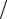
Q.
Рис. 5.4. Параллельный колебательный контур с последовательным (а) и параллельным (б) включением сопротивления потерь
Для описания частотно-избирательных свойств параллельного контура применяют комплексное входное сопротивление Z( j ) и частотные коэффициенты передачи по току Ki ( j ) и напряжению Ku( j ) – резонансные характеристики контура.
Комплексное входное сопротивление является основной характеристикой контура. Оно равно отношению комплексной амплитуды выходного напряжения к комплексной амплитуде тока в контуре. Определим эту характеристику для контура, изображенного на рис. 5.4, а:
|
Uвх |
|
|
1 |
(R j L) |
|
Z(j ) |
|
|
j C |
|||
|
|
. |
||||
I |
|
1 |
|
|||
|
|
|
|
|
R j L |
|
|
|
|
|
j C |
||
|
|
|
|
|
|
|
Полагаем, что потери в контуре малы. Это позволяет в области резонансной частоты считать, что R L. Тогда
Z( j ) |
|
L C |
|
|
|
|
L RC |
|
|
|
|
|
|
L RC |
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
L |
|
|
|
p |
|||||||||||||
|
R j |
L |
|
|
1 j |
|
L |
|
|
1 j |
|
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
R C |
|
|
|||||||||||||||||||
|
|
|
C |
|
|
R |
C |
|
|
|
|
p |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Как видно из данной формулы, при резонансе, когда p, входное со-
противление контура носит резистивный характер. Оно называется резонансным сопротивлением и равно
|
|
|
|
Z( j ) |
L |
|
2 |
Q2R R . |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
RC R |
|
|
0 |
|||||||
Продолжая преобразования формулы для Z( j ), получим |
|||||||||||||||
|
|
|
|
Z( j ) |
R0 |
|
R0 |
|
, |
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 j |
|
|
|
1 jQ |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
p |
|
|
|
|
|
R |
|
|
|
|
||
где |
|
|
– частотная расстройка, |
Q |
|
– обобщенная расстройка |
|||||||||
|
|
|
|||||||||||||
p |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
контура.
При малых расстройках в области частот, близких к резонансной ( p), можно записать
|
|
p |
|
2 2p |
|
2( p) |
2 |
||||
Q Q |
|
|
|
|
Q |
|
Q |
|
Q |
|
. |
|
|
|
|
|
|||||||
|
p |
|
|
|
|
p |
|
p |
p |
||
|
|
|
|
|
|||||||
Таким образом, комплексное входное сопротивление контура равно
|
|
Z( j ) |
R0 |
|
|
R0 |
|
|
e jarctgQ |
Z( )e j ( ). |
(5.5) |
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 jQ |
1 Q |
2 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Здесь |
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
Z( ) |
|
|
– модуль входного сопротивления контура. Зависимость |
|||||||||||
|
|
|
||||||||||||
1 Q2 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
модуля входного сопротивления контура от частоты является амплитудночастотной характеристикой контура;
( ) arctgQ – аргумент входного сопротивления контура. Зависимость аргумента входного сопротивления контура от частоты является фазо-частотной характеристикой контура.
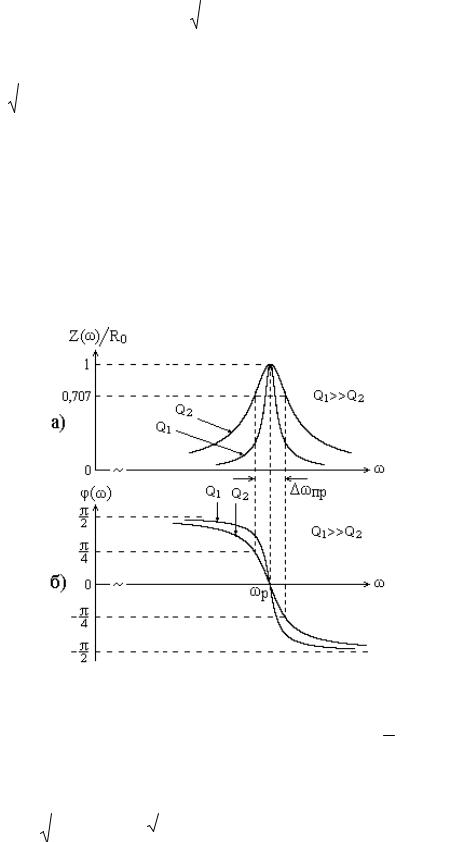
Амплитудно-частотная и фазочастотная характеристики параллельного колебательного контура при различных значениях добротности приведены на рис. 5.5.
Рис. 5.5. АЧХ (а) и ФЧХ (б) параллельного колебательного контура
Определим полосу пропускания контура на уровне 1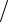
2:
|
R0 |
|
|
1 |
|
R ; |
Q2 2 1; |
|
пр |
|
p |
. |
|
|
|
|
|
|
|
|
|||||||
1 Q2 2 |
2 0 |
|
|
|
Q |
||||||||