4.2.3. Векторное представление сигнала с амплитудной модуляцией
Сигнал с амплитудной модуляцией можно представить в виде векторной диаграммы, которая наглядно отображает структуру сигнала и процесс изменения амплитуды несущего колебания. Наиболее просто векторная диаграмма получается для сигнала с однотональной амплитудной модуляцией. Воспользуемся спектральным представлением такого сигнала:
s(t) U |
н |
cos( |
t ) |
Uнm |
cos[( |
0 |
)t ] |
Uнm |
cos[( |
0 |
)t ]. |
|
|
||||||||||
|
0 |
2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
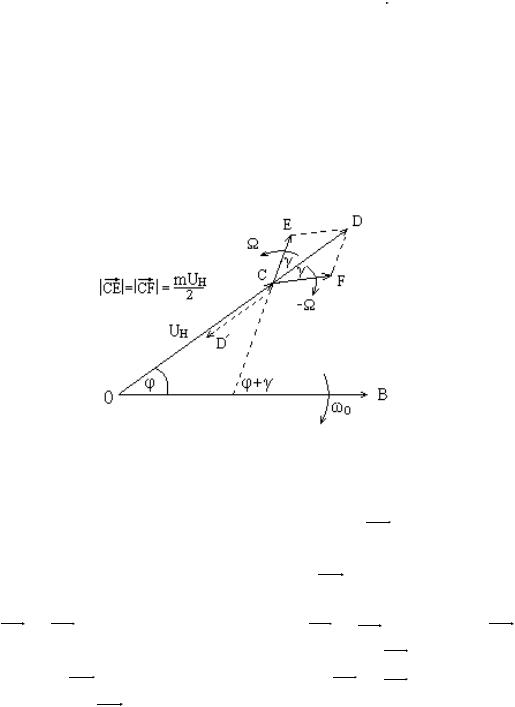
Первое слагаемое спектра изображается вектором OC длины Uн , составляющей угол с горизонтальной осью ОВ при t 0 (рис. 4.8). Вектор вращается против часовой стрелки с угловой скоростью 0.
Второе и третье слагаемые представляются векторами длины Uнm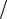
2, составляющими с линией ОВ углы соответственно г и г. Они вращаются против часовой стрелки со скоростями 0 и 0 .
Сумма проекций этих трёх векторов на горизонтальную ось ОВ и есть ам- плитудно-модулированное колебание s(t).
Рис. 4.8. Векторное представление АМ-сигнала
Для получения большей наглядности воспользуемся вращающейся системой координат. Для этого полагаем, что горизонтальная ось ОВ вращается по
часовой стрелке с угловой скоростью 0. Тогда вектор OC будет неподвижен, а векторы, изображающие верхнюю и нижнюю боковые составляющие, будут
вращаться со скоростью относительно вектора OC соответственно против и по часовой стрелке. Перенесём эти векторы параллельно самим себе в точку С и
обозначим CE и CF . (рис. 4.8). Сумма векторов CE и CF есть вектор CD, на-
зываемый вектором модуляции. Характерно, что вектор CD лежит на одной прямой с вектором OC, так как величины векторов CE и CF , а также их углы относительно вектора OC одинаковы. Вращаются эти векторы с одинаковой
скоростью (в разных направлениях). Вектор CD, величина которого изменя-
ется по мере вращения векторов CE и CF , прибавляется к вектору OC, обра-
зуя результирующий вектор OD с изменяемой длиной и направлением, совпа-
дающим с направлением вектора OC. Длина вектора OD изменяется периодически по мере вращения векторов боковых составляющих. Изменение длины этого вектора происходит от минимального значения Uн Uнm (при совпадении векторов боковых составляющих и их направлении, противоположном на-
правлению вектора Uн ) до максимального значения Uн Uнm (при совпадении векторов боковых составляющих и их направлении, совпадающем с направле-
нием вектора OC).
Проекция вектора OD на ось ОВ вращающейся системы координат соответствует сигналу s(t).
|
4.2.4. Энергетика АМ-сигнала |
Характерной особенностью амплитудно-модулированных колебаний явля- |
|
ется изменение |
амплитуды несущего колебания от минимального |
Umin Uн(1 m) |
до максимального Umax Uн(1 m) значений. В соответст- |
вии с изменением амплитуды изменяется и мощность от минимальной величины, равной
P |
|
Umin2 |
|
|
Uн2(1 m)2 |
|
P (1 m)2 |
, |
||
|
|
|
||||||||
min |
2 |
2 |
|
н |
|
|||||
до максимальной величины, равной |
|
|
||||||||
P |
|
Umax2 |
|
|
Uн2(1 m)2 |
P (1 m)2. |
||||
|
|
|
||||||||
max |
2 |
2 |
|
н |
|
|||||
|
|
|
|
|||||||
Здесь Pн Uн2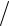
2 – мощность несущего колебания в отсутствие модуляции (в режиме молчания).
Таким образом, максимальным значениям огибающей соответствует мощ-
ность, в (1 m)2 раз большая мощности несущего колебания.
Средняя мощность периодического сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за период, и равна сумме средних мощностей гармонических составляющих его спектра. Ранее было показано, что для сигнала, спектр которого может быть представлен в виде
|
A0 |
|
|
s(t) |
Ak cos(k 1t k ), |
||
|
|||
2 |
k 1 |
||
средняя мощность равна
Pср A0 1 Ak2 ,
4 2 k 1
где Ak – амплитуда k -й гармонической составляющей.
Учитывая это, среднюю мощность рассматриваемого сигнала можно опре-
делить следующим образом |
2 2 |
|
|
|
|
|
2 2 |
|
0,5Uн2 1 0,5m2 . |
||||||
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|||||
Pср |
Uн2 |
|
|
m |
Uн |
|
|
|
m |
Uн |
|
||||
|
|
|
4 |
2 |
|
4 |
|||||||||
2 |
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно,
Pср 1 0,5m2 Pн.
Для оценки энергетики АМ-сигнала используют коэффициент полезного действия амплитудной модуляции, равный отношению мощности составляющих боковых частот к общей средней мощности сигнала, т.е.
|
0,5m2P |
m2 |
|||
|
н |
|
|
|
. |
|
m2 |
|
|||
|
Pср |
2 |
|||
Таким образом, средняя мощность амплитудно-модулированного сигнала в
1 0,5m2 раз больше средней мощности несущего колебания. Приращение мощности сигнала, обусловленное модуляцией (а именно оно определяет условия выделения сообщения при приеме), даже при предельной глубине модуляции, когда m=1, не превышает половины Pн. Учитывая, что при использовании амплитудной модуляции для передачи речевой или музыкальной информации коэффициент модуляции m не превосходит значения 0,3, можно сказать, что только 5% мощности излучаемого сигнала несут полезную информацию, содержащуюся в двух его боковых полосах, т.е. коэффициент полезного действия АМ-сигнала равен 0,05. Остальные 95% мощности приходится на несущую, которая никакой информации не несет. Общий вывод – амплитудная модуляция не является эффективной с энергетической точки зрения.
Информация о параметрах передаваемого сообщения содержится в каждой из боковых полос спектра АМ-сигнала. Она заключена в величинах амплитуд гармонических составляющих спектра, зависящих от коэффициента модуляции m, и в структуре боковых полос спектра. Данная особенность АМ-сигнала позволила создать альтернативные виды амплитудной модуляции – балансную и однополосную модуляцию.
4.2.5. Балансная амплитудная модуляция
Для эффективного использования мощности передатчика при амплитудной модуляции используют так называемую балансную амплитудную модуляцию. При такой модуляции формируется амплитудно-модулированный сигнал, спектр которого не содержит составляющей на несущей частоте. Поэтому такой
АМ-сигнал называют сигналом с подавлением несущей (английский термин – amplitude modulation with suppressed carrier, AM-SC ).
Радиосигнал с балансной модуляцией при тональном модулирующем сигнале имеет вид
s(t) |
Uнm |
cos[( |
0 |
)t ] |
Uнm |
cos[( |
0 |
)t ]. |
|
|
|||||||
2 |
|
2 |
|
|
||||
|
|
|
|
|
||||
Для получения такого сигнала достаточно перемножить несущее и модулирующее колебания. По существу в результате будут получены биения двух гармонических сигналов с одинаковыми амплитудами и частотами 0 и
0 (рис. 4.9).
Характерно, что при переходе огибающей сигнала через нуль фаза несущего колебания скачком изменяется на 1800, т.к. огибающая изменяет свой знак. Поэтому в высокодобротном колебательном контуре, на который подается сигнал с балансной модуляцией и несущей частотой 0, равной резонансной частоте контура, колебания с частотой 0 будут компенсировать друг друга в каждом периоде модулирующего колебания. Этим и объясняется отсутствие в спектре сигнала с балансной модуляцией составляющей с несущей частотой при наличии высокочастотного заполнения на осциллограмме сигнала.
Несмотря на то что КПД сигнала с балансной амплитудной модуляцией равен 1, этот вид модуляции не нашел применения в технике связи из-за сложности детектирования сигнала.
Рис. 4.9. Балансная амплитудная модуляция