алгоритмы и блок-схемы

1. АЛГОРИТМ

Узнавать о новых алгоритмах и учиться их применять — важная часть программистского образования

Говард Джонстон

Понятие "алгоритм" происходит от имени математика из Хорезма Мухаммеда бен Муссу, которого в Европе знали под именем аль-Хорезми (лат. algorithmi), жившего в 783-850 гг. и сформулировавшего правила сложения чисел, названные в его честь алгоритмом.

Алгоритм — конечная последовательность точно определенных действий (правил и команд), предназначенных для решения задачи.

“Алгоритм должен быть определен настолько четко, чтобы его указаниям мог следовать даже компьютер”, — Дональд Э. Кнут.

Примеры алгоритмов:

правила сложения, умножения, деления, возведения в степень;

решение уравнений;

вычисление площади и объема фигуры и т.д.

Алгоритм обладает следующими свойствами:

дискретность – алгоритм состоит из отдельных шагов;

конечность – завершение после определенного числа шагов;

массовость – пригодность для решения широкого класса задач;

понятность – однозначное понимание выполнения алгоритма.

Для описания алгоритма следует:

задать (ввести) исходные данные;

определить правило обработки информации и получения результата;

вывести результаты.

Алгоритмы могут записываться:

на естественном языке (словесно-формульный способ описания);

при помощи блок-схем (структурный способ описания);

с использованием специальных алгоритмических языков;

с помощью граф-схем (граф — совокупность точек и линий, в которой каждая линия соединяет две точки);

с помощью сетей Петри.

Перед составлением программ чаще всего применяют первый или второй способы записи алгоритмов.

При словесно-формульном способе описания алгоритм записывается последовательно в виде текста с формулами.

Например, алгоритм решения квадратного уравнения a·x2+b·x+c=0, где а≠0, записывается следующим образом:

1.ввести значения коэффициентов a и b;

2.найти дискриминант по формуле D = b2 — 4·a·c;

3.если дискриминант D > 0, то уравнение имеет два корня:

4. если дискриминант D = 0, то уравнение имеет один корень

x b

2a

5.если дискриминант D < 0, то уравнение не имеет корней;

6.вывести полученный результат.

1.1. Блок-схема алгоритма

Благодаря своей наглядности данный способ записи алгоритмов получил наибольшее распространение. При построении блок-схемы алгоритм изображается геометрическими фигурами (блоками), связанными линиями (направление потока информации) со стрелками. Внутри блоков записывается последовательность действий.

В таблице 1 приведены виды и назначение основных блоков, применяемых для составления блок-схемы алгоритма.

Таблица 1. Виды и назначение основных блоков

Правила оформления блок-схем:

в пределах одной схемы блоки изображают одинаковых размеров;

все блоки нумеруются (номер ставится в верхнем левом углу блока

сразрывом линии);

линии, соединяющие блоки и указывающие последовательность связей между ними, проводятся параллельно линиям рамки;

стрелка в конце линии не ставится, если линия направлена слева направо или сверху вниз;

из блока «условие» могут выходить две линии, из других блоков — только одна линия;

если схема занимает более одного листа, то в случае разрыва линии используется межстраничный соединитель;

внутри каждого соединителя указывается номер блока (откуда или куда направлена соединительная линия). Внутри межстраничного соединителя в первой строке указывается номер листа, во второй —номер блока куда или откуда передается управление.

В зависимости от поставленной задачи выделяют три основных вида алгоритмов:

линейный;

разветвляющийся;

циклический.

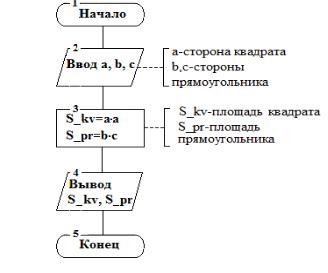
Линейным называется алгоритм, в котором все действия, указанные в блоках, выполняются по порядку их следования.

Пример блок-схемы алгоритма вычисления площадей прямоугольника и квадрата (рис. 1.1).

Рис. 1.1 Блок-схема линейного алгоритма

Разветвляющимся называют алгоритм, в котором в зависимости от значения условия (выполняется или не выполняется) изменяется последовательность выполнения действий алгоритма.

Пример блок-схемы алгоритма определения принадлежности точки с координатами (x, y) номеру сектора (рис. 1.2).

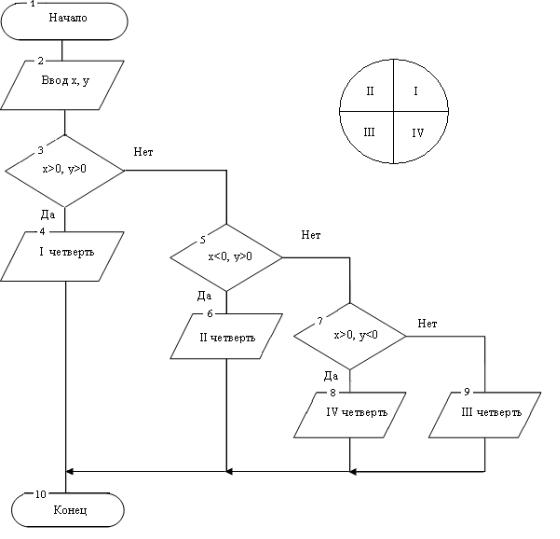
Рис. 1.2 Блок-схема разветвляющегося алгоритма

Циклическим называется алгоритм, в котором некоторая последовательность действий повторяется определенное количество раз.

Тело цикла – действия, выполняемые в цикле. Циклические алгоритмы могут быть:

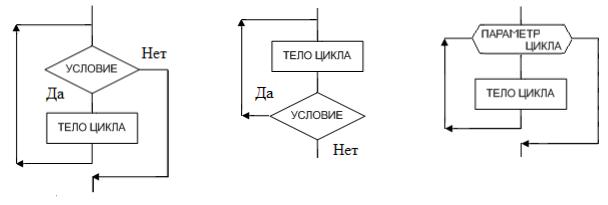
с предусловием – условие, при котором выполняется тело цикла, задается в начале цикла (рис. 1.3);

с постусловием – условие, при котором выполняется тело цикла, задается в конце цикла (рис. 1.4);

с параметром — в начале цикла задается правило изменения его параметра (рис. 1.5).

Пример блок-схемы циклического алгоритма нахождения НОД (наибольшего общего делителя) двух значений a и b.

Правило нахождения НОД (a, b) формулируется следующим образом:

1.определяется наибольшее из значений a и b — max (a, b);

2.из наибольшего значения вычитается оставшееся значение;

3.п.п. 1 и 2 повторяются до тех пор, пока значения a и b не станут

равными.

Полученное значение будет НОД (a, b).

a = b => НОД (a, b) =5

Составим блок-схему алгоритма нахождения НОД (a, b) (рис. 1.6):

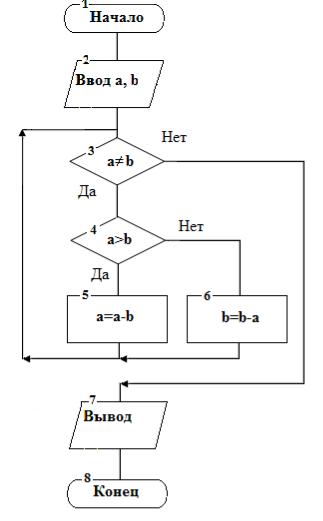
Рис. 1.6 Блок-схема алгоритма нахождения НОД (a, b).

Для реализации алгоритма на компьютере необходимо описать его на языке программирования.