5_MathCAD

2

Лабораторная работа 1

Основы работы в MathCAD

Цель работы: получить начальные навыки работы в среде MathCAD. Изучить интер-

фейс MathCAD.

Теоретическая часть

1. Окно Windows-приложения MathCAD

Интерфейс MathCAD внешне напоминает интерфейс таких приложений OC Windows, как MS Word, MS Excel или MS Access. Окно MathCAD включает, привычные для приложений Windows элементы: заголовок, главное меню, панели инструментов, горизонтальный и вертикальный скроллинг, окно редактирования и строку состояния. Новым элементом являются палитры операторов и шаблонов.

1.1. Палитры операторов и наборные панели

Они служат для ввода математических знаков (цифр, знаков арифметических и логических операций, знаков математических операций (интегралов, производных и т.д.)), греческих букв, шаблонов матриц и графиков. Значки палитр собраны на единой панели. Панель содержит значки палитр: арифметические операторы, операторы отношения, шаблоны графики, матричные операторы и шаблоны, операторы знаков высшей математики, операторы программ и греческие буквы. Если щёлкнуть мышью на значке палитры, то откроется наборное поле соответствующей палитры.

1.2Документ MathCAD

Вокне редактирования формируется документ MathCAD. Документ объединяет описание математического алгоритма решения задачи с текстовыми комментариями и результатами вычислений, заданными в форме чисел, таблиц и графиков. Новый документ получает имя Untitled - безымянный и порядковый номер. Одновременно открыто может быть до 8-ми документов.

Документ состоит из трёх видов областей: формульных, текстовых и графических. Области просматриваются системой, интерпретируются и исполняются. Просмотр идет слева направо и сверху вниз.

1.3Главное меню

Вторая строка окна MathCAD – главное меню. Оно содержит следующие пункты:

File (Файл) – для работы с файлами документов. Файлы документов в MathCAD имеют расширение .mcd. Пункт главного меню Файл содержит следующие команды:

Команды меню New (Создать), Open (Открыть), Close (Закрыть), Save (Сохранить),

Save As (Сохранить как….), , Page Setup (Параметры страницы), Print Preview (Про-

смотр), Print (Печать), Exit (Выход) имеют одинаковое назначение в приложениях работающих под Windows.

Collaboratory (Совместная работа), Internet Setup, Send (Отправить).

Пункт главного меню Edit (Правка). Команды в этом пункте служат для редактирования документов. MathCAD имеет общие с другими приложениями команды редактирования:

Undo (Отменить изменения), Redo, Cut (Вырезать), Copy (Копировать), Paste (Вста-

вить). Рассмотрим команды присущие только MathCAD.

Paste Spacial (Специальная вставка) – вставка объектов типа OLE с сохранением свойств редактирования.

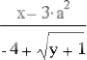
4

факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками.

Типы данных

К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа.

Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.

В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения. Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды

Математика Опции.

Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной. Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши : (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и её нельзя использовать. Однако с помощью знака ≡ (клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание. MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания (≡), а при втором – производятся действия, предписанные локальным оператором присваивания (:=), и отображаются все необходимые результаты вычислений (=).

Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства → (комбинация клавиш Ctrl + .).

2.2.1 Создание формульных областей

Для ввода формулы нужно установить указатель мыши в свободном месте окна редактирования и щелкнуть левой кнопкой мыши. Появится визир в виде красного крестика. Он указывает место, с которого начинается набор формулы. Например, для ввода формулы

нужно набрать на клавиатуре x-3*a^2 это числитель формулы. Так как все операнды числителя делятся на выражение знаменателя, нужно, нажимая на клавишу пробел, охватить кур- сором-уголком синего цвета весь числитель. Затем следует ввести знак /, чтобы создать дробную черту. Наберите -4+ и щёлкните на кнопке, помеченной символом √ на наборном поле арифметических знаков. Под знаком корня введите y+1.

Знаки операторов и шаблонов можно выбирать в наборных полях соответствующих палитр. Некоторые знаки можно также ввести с клавиатуры.

Дискретные аргументы - особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений, либо цело-

1.Установить визир в пустом месте рабочего документа.

2.Выбрать команду

Вставка График Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть

декартового графика.

3.Введите в средней метке под осью Х первую независимую переменную, через запятую – вторую и так до 10, например х1, х2, …

4.Введите в средней метке слева от вертикальной оси Y первую независи-

мую переменную, через запятую – вторую и т. д.,

например у1(х1), у2(х2), …, или соответствующие выражения.

5.Щёлкните за пределами области графика, что бы начать его построение.

6.Введите в средней метке под осью Х первую независимую переменную, через запятую – вторую и так до 10, например х1, х2, …

7.Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую – вторую и т. д.,

например у1(х1), у2(х2), …, или соответствующие выражения.

8.Щёлкните за пределами

области графика, что бы начать его построение.

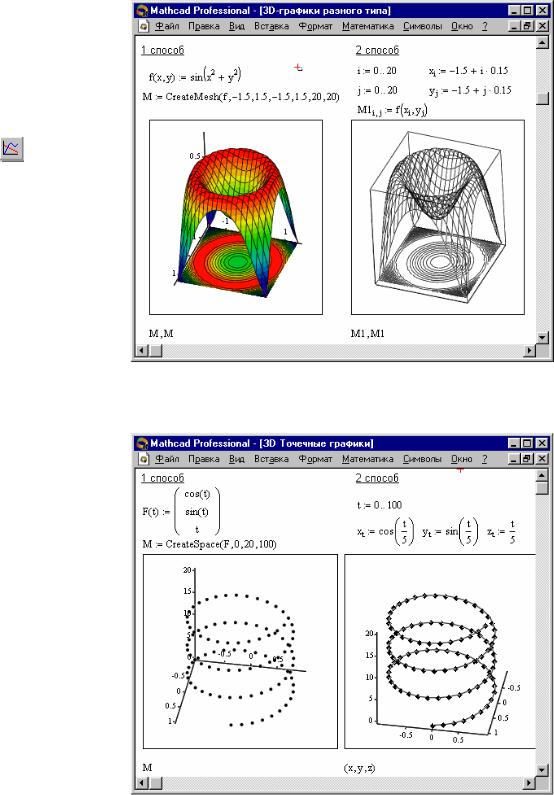
Трёхмерные, или 3D-

графики, отображают функции двух переменных вида Z(X, Y). При построении трехмерных графиков в ранних версиях MathCAD поверхность нужно было определить математически (Рисунок 2, способ 2).

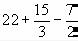
7

2.4 Редактирование документа

Редактирование документа состоит в перемещении или копировании областей в пределах документа, перемещении или копировании их в другой документ, вставки в документ или удаления из него строк. Любая из областей документа (текстовая, формульная, графическая) занимает прямоугольный участок. Для выделения области нужно щелкнуть мышью в любом месте области. Чтобы переместить эту область, необходимо установить указатель мыши на его границу. При этом указатель превратиться в стилизованную кисть руки. Затем следует нажать на левую кнопку мыши и, не отпуская ее, переместить выделенную область на новое место документа. Чтобы выделить несколько расположенных рядом областей, необходимо установить указатель мыши рядом с границей одной из них и нажать левую кнопку мыши. Далее не отпуская кнопку мыши, следует перемешать указатель мыши так, чтобы каждая из подлежащих выделению область частично или полностью попала бы в появившийся пунктирный прямоугольник. При этом границы всех выделенных областей помечаются пунктирной линией. Заметим, что если, отпустив левую кнопку мыши, перемешать указатель мыши, по при пересечении пунктирной границы любой области курсор мыши превратиться в стилизованную кисть руки. Если в этом случае «потянуть» мышь при нажатой левой кнопке, то все выделенные области будут перемещаться в направлении движения мыши.

Практическая часть

Для сокращения записи условимся обозначать клавиши, которые нужно нажимать на клавиатуре, угловыми скобками: например, <x> означает, что необходимо нажать клавишу х; <Shift>+<x> означает, что нужно нажать клавишу Shift и, не отпуская её, - клавишу х; <Space> - пробел; <Backspace> - удаление влево.

Задача 1. Вычислить арифметические выражения .

и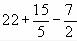

Решение:

1.Щёлкните мышью по любому месту в рабочем документе. Вы увидите крестик, обозначающий позицию, с которой начинается ввод.

2.Введите первое арифметическое выражение, последовательно нажимая клавиши на клавиатуре <2>, <2>, <+>, <1>, <5>, </>, <3>, <Space>, <->, <7>, </>, <2>. Обратите внимание на экран. Вы должны увидеть заданное выражение, обрамленное прямоугольной рамкой, причем число 2 выделено угловой рамкой (синего цвета).

3.Введите с клавиатуры знак равенства, нажав клавишу <=>, вы увидите после знака равенства мгновенно вычисленное значение выражения 23,5.

4.Щёлкните мышью справа внизу возле цифры 3. Вы увидите, что 3 выделено синей угловой рамкой. Нажмите <Backspace>. Вы увидите, что теперь значение выражения не определено, место ввода помечено черной меткой и ограничено угловой рамкой.

5.Введите с клавиатуры цифру 5 и щёлкните мышью вне выделяющей рамки (или нажмите <Enter>). Вы увидите измененное выражение и её значение 21,5.

6.Теперь удалите выражение. Щёлкните мышью по любому месту в выражении и нажимайте клавишу <Space> до тех пор, пока все выражение не будет выделено угловой синей рамкой. Нажмите <Backspace> (поле ввода окрасится в черный цвет) и, нажав клавишу <Del>, удалите выделенное. Выражение исчезнет с экрана.

7.Введите с клавиатуры второе арифметическое выражение.

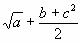
8

8.Найдите на экране панель математических инструментов MathCAD (группа из 8 кнокнопок с изображением калькулятора, графика, матрицы и т.п.). Если таковой не окажется, то щёлкните по пункту меню View, в открывшемся меню наведите мышь на строку Toolbar и пометьте строку Math. В панели математических инструментов щёлкните по кнопке с изображением черной шапочки. Откроется панель символьных вычислений. Щёлкните по кнопке с изображением стрелки (левая верхняя кнопка). Вы увидите соответствующий знак после выражения. Нажмите <Enter>. В результате вы увидите вычисленное значение выражения в виде обыкновенной дроби.

Замечание 1. Если при вводе выражения была допущена ошибка, выделите неправильный символ угловой рамкой (Щёлкните справа внизу возле символа), удалите выделенный символ (<Backspace>) и введите в помеченной позиции исправление.

Задача 2. Вычислить значение выражения

при a=2, b=3, c=4.

Решение:

1.Щёлкните мышью по свободному месту в рабочем документе.

2.Введите значение переменной а, нажимая последовательно клавиши <a>, <Shift>+<:>,<2>. Вы увидите после а знак присваивания “:=”.

3.Аналогично введите значения переменных b и с.

4.Ниже введенных значений a, b и с введите данное выражение, выполняя следующие

действия:

o щёлкните по кнопке с изображением калькулятора панели математических инструментов и в открывшейся панели Щёлкните по кнопке с изображением квадратного корня; вы увидите на экране соответствующий символ с помеченным место ввода подкоренного выражения;

o нажмите клавиши <a>, <Space>, <+>, <b>, <+>, <c>, <Shift>+<6>, <2>, <Space>, <Space>, </>, <2>, < = >; и Щёлкните по свободному месту вне поля ввода.

Замечание 2. MathCAD читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее или ниже определённых для него значений переменных.

Задача 3. Построить график функции

.

Решение:

1.Щёлкните по свободному месту в рабочем документе.

2.Введите функцию, последовательно нажимая клавиши <f>, <(>, <x>, <)>, <Shift>+<:>, <x>, <Shift>+<6>, <Space>, <+>, <8>, <*>, <x>, <+>, <1>.

3.Щёлкните по свободному месту в рабочем документе ниже введенной функции, затем

– по кнопке с изображением графика в панели математических инструментов и в открывшейся панели. Щёлкните по левой верхней кнопке. Появится поле для построения графика.

4.В нижнюю помеченную позицию введите с клавиатуры имя аргумента х, затем щёлкните по помеченной позиции с левой стороны, введите с клавиатуры f(x) и щёлкните вне прямоугольной рамки.

9

5.Щёлкните по пункту X-Y-Plot строки Graph меню Format. В появившемся окне настройки параметров изображения пометьте пункты Crossed и Equal Scales и щёлкните

OK.

6.Щёлкните по полю графика, затем – по числу, задающему наименьшее значение аргумента (число в левом нижнем углу ограниченного рамкой поля графиков), нажмите <Backspace> и введите с клавиатуры -20. Аналогично измените правую границу аргумента и границы изменения функции f(x). Щёлкните вне поля графика.

Задача 4. Вычислить значение функции:

при t=2.

Вычислите значения функции для всех t = 0,1,2,…,9.

Решение:

1.Щёлкните по свободному месту в рабочем документе.

2.Введите функцию. <Enter>.

3.Введите с клавиатуры <f>, <(>, <2>, <)>, < = >, <Enter>.

4.Введите с клавиатуры <t>, <Shift>+<:>, <0>, <;>, <9>, <Enter>.

5.Введите с клавиатуры <f>, <(>, <t>, <)>, < = >. В результате под именем функции появится таблица значений функции.

Задача 5. Решите уравнение:

.

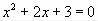Решение:

1.Щёлкните по свободному месту в рабочем документе.

2.Введите ключевое слово Given.

3.Ниже введите с клавиатуры уравнение, причём, при вводе знака равенства нажмите

<Ctrl>+< = >.

4.Ниже введите Find(x) ® (стрелка из панели символьных вычислений) и щёлкните <Enter>. В результате появится столбец, содержащий значения корней уравнения.

Замечание 3. Система уравнений можно решить также по схеме Given, уравнения, Find(x, y, …).

Замечание 4. Сохранение рабочего документа в файле, открытие нового рабочего документа, чтение рабочего документа из файла выполняются стандартным для ОС WI- NDOWS-приложений образом (с помощью меню File).

ЗАДАНИЯ

10