Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка.pdf

Скачиваний:

222

Добавлен:

11.05.2015

Размер:

4.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

где коэффициенты a,b, c, d, e, g, f есть функции только x и y.

Если коэффициенты уравнения (6.3) не зависят от x и y, то оно представляет собой линейное уравнение с постоянными коэффициентами.

Определение 6.4. Линейное уравнение (6.3) называется однородным, ес-

ли f (x, y) 0 для (x, y) D.

Определение 6.5. Решением уравнения (6.1) называется определенная в области D действительная функция u(x,y), непрерывная в этой области вместе со своими частными производными, входящими в уравнение, и обращающая его в тождество в области D.

§6.2. Классификация и приведение к каноническому виду линейных уравнений в частных производных второго порядка с двумя независимыми переменными в окрестности точки

Рассмотрим линейное уравнение

x, y,u,

(6.4)

x y

в котором коэффициенты a,b, c есть функции x и y, имеющие непрерывные частные производные до второго порядка включительно в области D.

Предположим, что a,b, c не обращаются одновременно в нуль и что функция u (x, y) имеет непрерывные частные производные до второго порядка

включительно в этой области.
	Определение 6.6.		Уравнение		(6.4)		называется			в некоторой точке
M0(x0, y0), M0 D, уравнением									M0
b2	1)	гиперболического типа, если				в	точке			выполнено условие
	ac 0;							M0 справедливо равенство
b2	2)	параболического	типа,	если	в	точке
	ac 0;							M0
	3)	эллиптического	типа,	если	в	точке			выполнено неравенство

b2 ac 0.

Определение 6.7. Кривая (x, y) c называется характеристикой урав-

нения (6.4) в некоторой точке M0(x0,y0), принадлежащей этой кривой, если выполнены следующие условия:

1) 2 (x0, y0) 2 (x0, y0) 0;

x2 y2

2 (x , y

)

2 (x , y

)

2) a(x , y

)

2b(x , y

)

x y

c(x0, y0)

2 (x0

y0)

Функция u (x, y)

является частным решением уравнения

x y

в том и только в

том случае,

когда кривая (x, y) c

есть общий интеграл

дифференциального уравнения

ady2 2bdxdy cdx2

(6.5)

Определение 6.8. Уравнение (6.5) называется характеристическим для

уравнения (6.4).

Пусть G некоторая окрестность точки M0(x0,y0),		в которой уравне-
ние (6.4) имеет один и тот же тип. В силу достаточной гладкости в области G
коэффициентов a, b, c всегда существует такое невырожденное преобразова-
ние
(x, y),	(x, y)	(6.6)

переменных x,y,

при помощи которого уравнение (6.4) в этой области приво-

дится к уравнению вида

u u

2 2b

, , u,

(6.7)

где

( , ) a

x y

c( , ) a

b( , ) a

x x

x y

причем b2

(b2

ac)

, т. е.

(6.8)

c				,

y y

преобразование (6.6) не

меняет типа уравнения.

Выясним, какое преобразование (6.6) приводит в некоторой окрестности G точки M0(x0,y0) уравнение (6.4) к уравнению (6.7) наиболее простой формы в каждом из трех указанных случаев.

b2 ac 0

Пусть

сначала

b2 ac 0 в

области G. Будем считать,

что

в точке

M0(x0,y0)

либо a 0, либо c 0.

В противном случае этого можно достиг-

нуть заменой переменных x

y x

Рассмотрим уравнение

(6.9)

Предположим,

что

a 0

в точке M0(x0,y0),

тогда в силу

условия

b2 ac 0 уравнению (6.9) удовлетворяют решения каждого из уравнений:

b2 ac

(6.10)

Кривые 1(x, y) c,

2(x, y) c представляют собой действительные и

различные характеристики уравнения (6.4) гиперболического типа.

Так как a 0, то из (6.10) следует, что в некоторой окрестности G точки

M0(x0,y0)

выполнены условия

и, значит,

преобразова-

ние 1 (x, y), 2 (x, y) в этой окрестности является невырожденным.

Указанное преобразование приводит в окрестности G точки M0(x0,y0)

уравнение (6.4) к уравнению (6.7), в котором a c 0, b 0, т. е. к уравнению вида

2u
	F	, , u,
	F	, , u,
	3

u		u
	,		.	(6.11)

Пусть , , тогда уравнение (6.11) примет вид

2u		2u				u		u
				F	, , u,		,		,	(6.12)
	2		2
				4

который называется каноническим видом уравнения гиперболического типа.

Пусть теперь в области G. Тогда хотя бы один из коэффициентов a, c отличен от нуля в этой области. Предположим, например, что a 0

в точке M0(x0,y0), следовательно, оба уравнения (6.10) совпадают и обращаются в уравнение


a		b		0.	(6.13)

	x		y

Если функция 1(x, y) – решение уравнения (6.13), имеющее непрерывные частные производные второго порядка, и первые производные этой функции

не обращаются в нуль одновременно в области G, то кривая 1(x, y) с является действительной характеристикой уравнения (6.4) параболического типа.

Положим

1 (x, y), 2 (x, y), (6.14)

где 2 (x, y) – любая дважды непрерывно дифференцируемая в области G функция, такая, что преобразование (6.14) является невырожденным в этой области.

Тогда уравнение (6.4) приводится к уравнению (6.7), где a b 0, c 0

в G, т. е. к уравнению вида
	2u				u		u

		2 F5		, ,u,		,
		2 F5		, ,u,		,		,

которое называется каноническим видом уравнения параболического типа.
Пусть, наконец, в области G выполнено условие b2 ac 0. Предполо-
жим, что все коэффициенты a, b,			c	есть аналитические в этой области функ-

ции от x и y. Тогда коэффициенты уравнений (6.10) – также аналитические функции от x и y в области G. Пусть (x, y) 1(x, y) i 2(x, y) есть ана-

литическое решение первого из уравнений (6.10) и				0 в этой об-
		x	y

ласти. Тогда кривые 1(x, y) i 2(x, y) c	являются		комплексно-сопря-
женными характеристиками уравнения (6.4)	эллиптического типа. Полагая

1(x, y), 2(x, y), получим невырожденное в G преобразование, кото-

рое приводит уравнение (6.4) к уравнению (6.7), где									a		с	,	b 0, т. е. к урав-
нению вида
	2u		2u				u		u
					F	, ,u,		,		,
		2		2	F	, ,u,		,		,
		2		2	6

и называется каноническим видом уравнения эллиптического типа.

§6.3. Уравнение малых поперечных колебаний струны. Граничные

иначальные условия. Корректность постановки задачи

Куравнениям гиперболического типа приводят задачи, связанные с процессами колебаний, например, задачи о колебаниях струны, мембраны, газа, электромагнитных колебаниях. Характерной особенностью процессов, описываемых такими уравнениями, является конечная скорость их распространения.

Рассмотрим задачу о колебаниях струны. Будем предполагать, что смещения струны лежат в одной плоскости (x, u) и вектор смещения u перпенди-

кулярен в любой момент к оси x. Тогда процесс колебания можно описать одной функцией u (x,t), характеризующей вертикальное перемещение струны.

Будем рассматривать струну как гибкую упругую нить и, значит, считать, что струна не сопротивляется изгибу.

Величина натяжения T0 в каждой точке не меняется со временем. Пусть(x) – линейная плотность струны и внешняя сила непрерывно распределена с плотностью F(x, t), рассчитанной на единицу длины.

В случае постоянной плотности const указанные колебания струны описываются уравнением вида

f (x,t),

(6.15)

где a

f (x,t)

F(x, t)

есть плотность силы,

отнесенная к единице

массы. Если внешняя сила отсутствует, то получаем однородное уравнение

(6.16)

характеризующее свободные колебания струны, которое является простейшим примером уравнения гиперболического типа.

Дифференциальные уравнения в частных производных имеют, вообще говоря, бесконечное множество решений. Для однозначной характеристики процесса необходимо к уравнению присоединить некоторые дополнительные условия.

Если рассматриваются поперечные колебания струны, закрепленной на

концах x 0	и x l в области	0 x l,			то должны выполняться граничные
условия	u (0, t) u (l,t) 0.					(6.17)

Так как процесс колебаний струны зависит от ее начальной формы и рас-
пределения скоростей, то следует указать начальные условия
	u (x,t0) (x),

	u (x,t0)
			(x),

		t

где (x), (x) есть заданные функции.
Если концы струны движутся по определенному закону, то граничные ус-
ловия (6.17) принимают вид
	u (0,t)			1	(t),	(6.18)

	u (l,t) 2 (t),
в котором 1	(t) и 2 (t) есть заданные функции времени t.
Определение 6.9. Краевая задача для уравнения (6.15) – задача нахожде-
ния функции	u (x,t), определенной в области 0 x l, t 0,					и удовлетво-

ряющей уравнению (6.15) для 0 x l,	t 0, граничным условиям (6.18) при
t 0 и начальным условиям

u (x,t)

u (x,0) (x),

		(6.19)
u (x,0)		(6.19)
u (x,0)		(x)
	t	(x)
	t

при 0 x l.

Если колебания происходят в течение малого промежутка времени, то влияние границ еще несущественно; поэтому вместо краевой задачи можно рассматривать предельную задачу с начальными условиями для неограничен-

ной области.
Определение	6.10. Задача	Коши	–	это	задача	нахождения функции
u (x,t), определенной в области:		x ,			t 0, удовлетворяющей урав-
нению (6.15) для	x ,	t 0,	и	начальным		условиям (6.19) при

x .

Решения краевой задачи и задачи Коши зависят от функций, входящих в начальные и граничные условия, которые на практике являются результатом некоторых измерений, поэтому неизбежны погрешности в их определении. Эти погрешности влияют на погрешности решений. Малые ошибки в начальных и граничных условиях могут повлечь за собой большую ошибку в решении. Различают корректно и некорректно поставленные задачи.

Определение 6.11. Краевая задача (6.15), (6.18), (6.19) называется корректно поставленной, если решение всегда существует для любых

f (x, t), 1 (t), 2 (t), (x), (x), однозначно определено и непрерывно зависит от исходных данных этой задачи.

Задачи, не удовлетворяющие перечисленным условиям, называются не-

корректно поставленными.
§6.4. Решение уравнений свободных колебаний
однородной струны методом Даламбера
Рассмотрим задачу Коши
		2u	a2	2u	,	(6.20)
		t2	a2	x2	,	(6.20)
		t2		x2
u (x, 0) (x),
	u (x, 0)			x ,		(6.21)
	u (x, 0)			x ,		(6.21)
		(x),
		(x),
	t
	t
описывающую свободные колебания однородной струны.
Учитывая, что	x at c1,		x at c2 – характеристики			уравнения
(6.20), введем новые переменные

x at, x at.

	2u		u

Тогда уравнение (6.20) примет вид		0 или		0.

Отсюда		g( ), где			g( ) – некоторая функция только переменной
Отсюда		g( ), где			g( ) – некоторая функция только переменной

и, значит, u( , ) g( )d f1 ( ) f1( ) f2							( ), в котором		f1 ( ) и
f2 ( ) есть функции только переменных и соответственно.
Следовательно,			u(x, t) f1(x at) f2(x at)
			u(x, t) f1(x at) f2(x at)
является решением уравнения (6.20).
Определяя функции f1					и f2 через заданные функции и ,				в силу на-
чальных условий (6.21) получим
			1		1			x at
	u (x, t)			[ (x at) (x at)]				( ) d .	(6.22)
	u (x, t)		2	[ (x at) (x at)]				( ) d .	(6.22)
			2			2a x at

Формула (6.22) называется формулой Даламбера и дает решение задачи Коши (6.20), (6.21), если (x) имеет непрерывные производные до второго порядка включительно, а (x) – до первого.

Задача Коши (6.20), (6.21) является корректно поставленной. Пример 6.1. Задача Коши:

	2u		2u			u(x, 0)
				,	u(x, 0) sin x,			x cosx.
	t2		x2			t
Решение.		В нашем случае (x) sin x,					(x) x cos x. Тогда

(x at) sin(x at) sin xcosat cos xsin at,

и, значит,

[ (x at) (x at)] sin xcosat .

x at

Найдем

( )d , получим

x at

( )d

( cos )d

sin

(x at)2

x at

(x at)2

x at

sin(x at)

sin(x at) 2a xt 2cosxsinat.

Отсюда в силу формулы (6.22) решение искомой задачи Коши имеет вид

u(x, t) sin xcosat xt cosxsinat. a

§6.5. Решение уравнений колебаний струны методом Фурье

6.5.1.Рассмотрим краевую задачу

2u a2 2u ,

t2 2x

u(0, t) u(l, t) 0, t 0,

u (x, 0) (x),
	u (x, 0)		0 x l,

		(x),

	t

(6.23)

(6.24)

(6.25)

описывающую свободные колебания однородной струны с закрепленными концами.

Будем сначала искать частные решения уравнения (6.23), не равные тождественно нулю, в виде произведения

u(x, t) X (x)T (t),

(6.26)

удовлетворяющие граничным условиям (6.24). Подставляя (6.26) в уравнение

(6.23), получим

T			2	T(t)	X
	(t) X(x) a					(x)
или		T (t)	X (x)

					.	(6.27)
			X(x)
		a2 T(t)

Левая часть последнего равенства зависит только от t, а правая – только от x, и равенство (6.27) возможно лишь в том случае, если левая и правая его части не зависят ни от x, ни от t, т. е. представляют собой одну и ту же постоянную, которую обозначим через ( ):

T (t)		X (x)
			.	(6.28)
a2
	T (t)	X(x)

Из соотношения (6.28) получаем два обыкновенных дифференциальных уравнения для определения функций X(x) и T(t):

X (x) X(x) 0,

(6.29)

		2	T(t) 0.		(6.30)
T (t) a
В силу граничных условий (6.24) получим
u(0, t) X	(0)T(t) 0,			t 0.
u(l, t) X (l)T(t) 0, t 0.
Отсюда следует, что функция	X(x) должна удовлетворять дополнитель-
ным условиям
X(0) X(l) 0,					(6.31)
так как в противном случае T(t) 0,			и, значит,	u (x, t) 0, что противоречит

задаче о нахождении нетривиального решения.

Найдем теперь те значения , при которых существуют нетривиальные решения задачи

X
	(x) X(x) 0,	(6.32)
	(0) X(l) 0.
X

Возможны следующие случаи: 1) 0; 2) 0; 3) 0. 1. При 0 общее решение уравнения (6.29) имеет вид

X(x) c1 e x c2 e x ,

где c1, c2 – произвольные постоянные. В силу условий (6.31) получим

c1 c2 0, c1 e l c2 e l 0.

Отсюда c1 c2 0, и, значит, X(x) 0.

2. При 0 общее решение уравнения (6.29) запишется в виде

X(x) c1 c2 x.

Тогда в силу (6.31) имеем c1 0, c1 c2 l 0, т. е. c1 c2 0, и, следовательно, X(x) 0.

3. При 0 общее решение уравнения (6.29) имеет вид

X(x) c1 cos 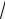x c2 sin x.

Учитывая условия (6.31), получим

c1 0,

c1 cos l c2 sin

l 0.

Если X(x) 0,

то c2 0,

поэтому sin l 0, т. е.

, n Z.

Следовательно, нетривиальные решения задачи (6.32) возможны лишь

n 2

при значениях n

n Z, n 0.

Этим значениям соответствуют функции

n Z, n 0,

Xn sin

определяемые с точностью до произвольного множителя, который положим равным единице.

В дальнейшем для n достаточно брать только целые положительные зна-

чения, так как n

n , а функции

X n

и Xn отличаются лишь постоянным

множителем.

При n , n N , общее решение уравнения (6.30) имеет вид

Tn(t) An cos

Bn sin

(6.33)

где An, Bn – произвольные постоянные. Таким образом, функции

un (x,t) Xn (t)Tn (t)

(6.34)

cos

sin

являются частными решениями уравнения (6.23), удовлетворяющими граничным условиям (6.24).

В силу линейности и однородности уравнения (6.23) сумма частных решений

u(x, t) u

(x,t) A

cos

sin

at sin

(6.35)

n 1

также является решением уравнения (6.23), удовлетворяющим граничным условиям (6.24), если ряд (6.35) равномерно сходится и его можно дважды по-

членно дифференцировать по x и

u (x,t)

Определим коэффициенты

из условия, что функция

удовлетворяет начальным условиям (6.25).

Продифференцируем ряд (6.35) по переменной t:

A sin

cos

at sin

x .

(6.36)

n 1 l

Полагая в (6.35) и (6.36) t

0, получим в силу начальных условий (6.25):

(x)

An sin

n 1

(6.37)

a Bn sin

(x)

n 1

Формулы

(6.37) представляют

собою

разложения

заданных функций

(x) и (x) в ряд Фурье по синусам в интервале (0, l). Отсюда

(x)sin

x dx,

n N .

(6.38)

(x)sin

dx,

Таким образом, решение краевой задачи (6.23) – (6.25) определяется рядом (6.35), где коэффициенты An и Bn вычисляются по формулам (6.38).

Если функция (x) на отрезке [0, l] дважды непрерывно дифференци-

руема, имеет кусочно-непрерывную третью производную и удовлетворяет условиям (0) (l) 0, (0) (l) 0, а функция (x) на этом отрезке

непрерывно дифференцируема, имеет кусочно-непрерывную вторую производную и удовлетворяет условиям (0) (l) 0, то функция u (x,t), определяемая рядом (6.35), имеет непрерывные производные второго порядка и

удовлетворяет уравнению (6.23), граничным условиям (6.24) и начальным условиям (6.25). При этом возможно почленное дифференцирование ряда (6.35) по x и t два раза, и полученные ряды сходятся абсолютно и равномерно при 0 x l и любом t 0.

Пример 6.2. Решите краевую задачу

u(0, t) u(l,t) 0,

u(x, 0)

sin

3 x

u(x, 0)

Решение. В нашем случае (x)

sin

3 x

(x) 0. Найдем коэф-

n N .

фициенты An и Bn

по формулам (6.38). Так как (x) 0, то Bn 0,

Определим теперь An.

2 l

3 x

(x) sin

xdx

sin

xdx

l	1		3 n


	2	cos		l
0

		3 n
x	cos

			l

		1
			,еслиn 3,

x
	dx 8
				еслиn 3.
		0,

Следовательно, учитывая формулу (6.35), решение искомой краевой задачи имеет вид

u (x, t) cos

sin

6.5.2. Рассмотрим теперь краевую задачу

f (x, t),

(6.39)

u(0, t) u(l, t) 0,

t 0,

(6.40)

u(x,0) (x),

u(x,0)

0 x l,

(6.41)

(x),

описывающую вынужденные колебания однородной струны, закрепленной на концах.

Решение этой задачи будем искать в виде суммы

u v w,

(6.42)

где v есть решение неоднородного уравнения

	2v	a2	2v	f (x,t),		(6.43)
	t2		x2

удовлетворяющее граничным условиям
v(0,t) v(l,t) 0,					t 0,	(6.44)

и начальным условиям

v(x, 0)

v(x, 0)		0,	0 x l,	(6.45)

аw есть решение однородного уравнения

		2w		a2	2w	,	(6.46)
		t2		a2	x2	,	(6.46)
		t2			x2
удовлетворяющее граничным условиям
w(0, t) w(l, t) 0,						t 0,	(6.47)
и начальным условиям
w(x, 0) (x),
	w(x, 0)				0 x l.		(6.48)
	w(x, 0)				0 x l.		(6.48)
			(x),
			(x),
	t

Решение w представляет свободные колебания однородной струны, закрепленной на концах, и, значит, в силу формул (6.35), (6.38) имеет вид

w(x,t)

cos

sin

at sin

x ,

(6.49)

n 1

где

2 l

(x)sin

dx,

n N.

(6.50)

2 l

(x)sin

dx,

na 0

Решение v представляет вынужденные колебания однородной струны, закрепленной на концах, с отсутствующими начальными возмущениями.

Как и в случае свободных колебаний, решение v будем искать в виде ряда

	n
v(x, t) Tn(t)sin			x		(6.51)

		l		,
n 1

и, значит, граничные условия (6.44) выполняются, если ряд (6.51) сходится равномерно.

Определим теперь функции Tn (t) так, чтобы ряд (6.51) удовлетворял уравнению (6.43) и начальным условиям (6.45).

Подставляя ряд (6.51) в уравнение (6.43), имеем

na 2

(t)

(6.52)

sin

x f (x, t).

n 1

Разложив функцию f (x, t)

в ряд Фурье по синусам в интервале (0,l),

рассматривая t как параметр, получим

f (x, t) fn(t)sin

(6.53)

где

n 1

2 l

n N.

fn(t)

(6.54)

f (x,t)sin

x dx,

f (x,t),

Сравнивая разложения (6.52) и (6.53) для одной и той же функции

составим дифференциальные уравнения

na 2

(t)

fn(t),

n N,

(6.55)

определяющие функции Tn (t).

Чтобы решение v, определяемое рядом (6.51), удовлетворяло и начальным условиям (6.45), достаточно потребовать выполнения равенств

			T (0) T (0) 0,					n N.			(6.56)
				n	n
Решение уравнения (6.55), удовлетворяющее начальным условиям (6.56),
имеет вид		l				na
		l		t		na
										n N.
Tn	(t)				fn( )sin			(t )			(6.57)
Tn	(t)				fn( )sin		l	(t )	d ,		(6.57)
		na 0					l

Подставляя найденные выражения для Tn(t) в ряд (6.51), получим решение задачи (6.43) – (6.45), если ряд (6.51) и ряды, полученные из него почленным дифференцированием по x и t до двух раз включительно, равномерно сходятся. Последнее возможно, если непрерывная функция f (x,t) имеет непрерывные част-

ные производные по x до второго порядка и при всех t 0 выполнены условия f (0, t) f (l,t) 0.

Таким образом, решение искомой задачи (6.39) – (6.41) имеет вид

u(x, t) Tn

n 1

n					n
(t) sin		x		A	cos		at

	l		n 1	n		l

		n			n
B	n	sin		at sin

			l			l

			n			(6.58)
x		A cos			at

	n 1	n		l

l t

Bn sin

fn ( ) sin

(t )

sin

na 0

где коэффициенты An, Bn,

fn(t)

вычисляются по формулам (6.50) и (6.54).

Пример 6.3. Решите краевую задачу

e t sin

u(0, t) u(l, t) 0,

t 0,

u(x, 0) 0,

u(x, 0)

0 x l.

sin

Решение. В нашем случае (x) 0, (x) sin

f(x,t) e t sin

Тогда

2 l

(x)sin

n N .

dx 0,

Найдем теперь Bn, получим

2 l

(x)sin

sin

x dx

na 0

3 n

, если n 3.

cos

x dx 3 a

если n 3.

Определим коэффициенты

fn(t),

n N , по формуле

(t)

f (x, t)sin

2e t

sin

Тогда в силу формулы (6.58) имеем

l		t					n
e			sin		x	sin


0				l			l
				e t , если n 1.
x
	dx				если n 1.
				0,

x dx

l t

u(x, t)

sin

(t )

sin

d sin

3 a

a 0

Вычислим сначала полученный интеграл

u e

, d u e d ,

sin

)

(t )

cos

(t )

cos

(t ) d

u e ,du e d ,

cos

sin

)

l t

sin

(t ) d

a 0

cos

sin

2a2

Отсюда

l a e t

cos

l2 sin

2a2

Значит, решение искомой краевой задачи имеет вид

u(x, t)

sin

3 a

e t cos

sin

6.5.3. Рассмотрим краевую задачу

f (x, t),

(6.59)

u(0,t) 1	(t),	t 0,	(6.60)
	(t),
u(l,t) 2

u(x, 0) (x),
	u(x, 0)		0 x l,	(6.61)

		(x),

	t

описывающую вынужденные колебания однородной струны, концы которой x 0 и x l движутся по определенному закону (6.60).

Решение. Задачу (6.59) – (6.61) можно свести к задаче с однородными граничными условиями.

Введем новую вспомогательную функцию

w(x,t) 1(t) ( 2(t) 1(t))	x
		.	(6.62)
	l

Тогда

w(0, t) 1	(t),	t 0.
	(t),
w(l, t) 2
Решение задачи (6.59) – (6.61) будем искать в виде суммы
u v w,
где v есть новая неизвестная функция.
В силу граничных условий (6.60) и (6.63) функция v(x, t)
однородным граничным условиям
v(0, t) v(l, t) 0,		t 0.

Учитывая начальные условия (6.61), получим

(6.63)

(6.64)

удовлетворяет

(6.65)

v(x,0)

	t

				x
u(x,0) w(x,0) (x) 1(0) ( 2(0) 1(0))					1(x),
				l				(6.66)
	u(x,0)	w(x,0)	(x) 1(0) ( 2(0) 1(0))			x

							1(x),
	t	t
						l

где 0 x l.

Подставляя (6.64) в уравнение (6.59), имеем

f (x, t)

или

g (x, t),

(6.67)

где g (x, t)

f (x, t) 1(t) ( 2(t) 1(t))

Таким образом, функция v (x, t) является решением задачи

g (x,t),

v (0, t) v(l,t) 0, t 0,

v (x, 0) 1(x),

v (x, 0)

0 x l,

1(x),

и, следовательно, в силу (6.58), (6.50), (6.54) функция имеет вид

v(x, t)

cos

B sin

n 1

(6.68)

l t

gn( )sin

(t ) d

sin

где

2 l

1(x)sin

dx,

l 0

1(x)sin

n N.

(6.69)

dx,

gn(t)

2 l

l 0

	n
g(x, t)sin			x

		l		dx.

Отсюда решение искомой краевой задачи (6.59) – (6.61) запишется в виде

u(x, t) (t) (

(t) (t))

cos

n 1

(6.70)

sin

( ) sin

) d sin

в котором коэффициенты An,Bn,gn(t), n N, определяются по формулам (6.69).

Пример 6.4. Решите краевую задачу

u (0, t) e t ,

u (l, t) 0, t 0,

u (x, 0) 0,

0 x l.

u (x, 0)

Решение. В нашем случае

(x) 0, (x)

, f (x,t) 0, (t) e t

(t) 0.

Найдем по формулам (6.69) коэффициенты An, Bn, gn(t), n N . Учиты-

вая, что

1 (x)

1, 1(x) 1,

g (x, t) e

получим

	2 l		x		n
An

				1 sin		l
	l	0	l

cos

l x

cos

1 cos

n l

n 0

2		2		sin	n	x	l


	n		2n2		l		0

	2		l
Bn				sin


		na 0

gn(t

( 1)

1 ( 1)

n 1

;

2 l

2e t

)

sin

Тогда в силу формулы (6.70) имеем

1 ( 1)

n 1

u(x, t) e

cos

sin

n 1

l t 2e

sin

)

sin

na 0

Вычислим полученный интеграл. Обозначим

I e

sin

(t )

d ,

тогда

l na

e t cos

l2 sin

l2 ( na)2

Таким образом, решение искомой задачи имеет вид

1 ( 1)

sin

u(x, t) e

n 1

cos

n 1

l2 na e t

cos

a t l3 sin

a t

sin

( na)

( n)

Методические указания к выполнению контрольной работы

Задача 1. В пространстве R3 задан базис:

g1 (1; 1;1), g2 (2; 3; 4), g3 (2; 2; 6).

Построить по данному базису ортонормированный.

Решение.

Следуя процессу ортогонализации Грамма–Шмидта (1.1), положим

																															(12) f							1 ,
															f	1			g	1 (1; 1;1),							f2	g	2		(12) f							1 ,
где

							(f1,								2 )							1 2 ( 1)( 3) 1 4
			(12)										g
													g																			3 f2 ( 1;0;1).

														2											(	3 )2
										f1
										f1
	Далее
					f						3			(13) f1							(23) f2 , где
					f	3			g		3			(13) f1							(23) f2 , где
																				,				3 )
																	( f													(f			2	,			3 )
								(3)									( f		1				g		2; (3)					(f			2	,	g		3 )		2,
								(3)																	2; (3)														2,
							1																2				2									2
							1												f1				2				2						f2			2
																			f1														f2

тогда f		3	(2; 4; 2). Нормируя теперь векторы f1,																												f2, f3, получаем ОНБ:
			1				1						1													1	1													1		2		1
e				;								;						, e									;0;				,			e							;		;		.


1			3				3						3							2						2	2							3						6		6		6
			3				3						3													2	2													6		6		6

Чтобы убедиться в правильности вычислений, нужно найти попарные скалярные произведения полученных векторов. Все они должны быть нулевыми.

Задача 2. Найти прямое преобразование Фурье функции

		ax
	f (x) e		,	t 0
Решение.	0,			t 0.
Решение.
В соответствии с формулой (2.1) находим
					e (a i )t		1
					e (a i )t		1
F(i ) e at e i t dt e (a i ) tdt								.
F(i ) e at e i t dt e (a i ) tdt					a i			.
0	0				a i	0	a i
	/2					0
	/2
Задача 3.1. Вычислить интеграл		sin5 xcos3 xdx.
Решение.		0
Решение.
По формуле (3.12) имеем

													5 1					3 1
/ 2

			5		3			1					2						2									1 3 2									1 2 1					1
			5		3			1					2						2									1 3 2									1 2 1					1
	sin			xcos		xdx																																					.
	sin			xcos		xdx							5 3														2				5						2			4!		24	.
	0							2					5 3														2				5						2			4!		24
	0																1
																	1
															2
															2

																								x3					dx.
			Задача 3.2. Вычислить интеграл


																			0		(1 x)7
			Решение.
			По формуле (3.13), учитывая (3.9), имеем																															5
																																		5

							3							3/ 2												5/2 1

						x							x										x													(1)
						x				dx			x			dx							x								dx			2						2	.

												(1 x)7/ 2									(1 x)5/2 1																	7

				0 (1 x)				7			0									0																				5
											0									0


																											p											2
																			1						1		p
			Задача 3.3. Вычислить интеграл																	ln							dx,					p 1.
			Задача 3.3. Вычислить интеграл																	ln							dx,					p 1.
																									x
			Решение.																0						x
			Решение.
							сделаемзамену
							сделаемзамену
1		1		p			ln		1	t x e t ,dx e tdt																	0			p		t			p				t
		1		p			ln			t x e t ,dx e tdt																				p		t			p				t
	ln			dx					x																	t					e		dt t				e			dt (p 1).
	ln	x		dx					x																	t					e		dt t				e			dt (p 1).
0		x					x 0 t																											0
							x 1 t 0
			Задача 4.1. Решить линейное разностное уравнение второго порядка
														y(n 2) y(n) 2n																												(1)
при начальных условиях y(0) y(1) 0.
			Решение.
			Пусть												y(n) Y(z).																											(2)
															y(n) Y(z).																											(2)
			Тогда								y(n 2) z2[Y(z) (y
											y(n 2) z2[Y(z) (y															0		y		/ z)].												(3)
																										0	1													1 уравнения
			Комбинируя соотношения (2)														и (3) с коэффициентами 1,																							1 уравнения
(1) и учитывая, что выражение															y0 y1 / z							равно нулю в силу начальных усло-
вий, получим
			– для левой части (1): y(n 2) y(n) Y(z)(z2																													1);

– для правой части (1): 2n z . z 2

Операторное уравнение

Y(z)(z2 1) z z 2

имеет решение

Y(z)

(z2 1)(z 2)

Здесь особые точки z1 1, z2 1,z3 2. Тогда по формуле (4.3) находим

( 1)n

y(n) ResY(z) zn 1

ResY(z) zn 1

z 1

z 2

Задача 4.2. Решить линейное разностное уравнение второго порядка

y(n 2) 5y(n 1) 6y(n) 1

(4)

при начальных условиях y(0) 1, y(1)

Решение.

Пусть

y(n) Y(z).

(5)

Тогда

y(n 1) z[Y(z) y0] z[Y(z) 1];

(6)

y(n 2) z2[Y(z) y

/ z] z2

[Y(z) 1 1/ z].

(7)

Умножая соотношения (5) – (7) соответственно на 6, –5, 1, получим

y(n 2) 5y(n 1) 6y(n) Y(z)[z2 5z 6] (z2 5z) z.

Для правой части уравнения (4) будем иметь 1

Операторное уравнение

z 1

Y(z)[z2 5z 6] (z2 5z) z

z 1

имеет решение

z3 7z2 7z

7z2 7z

Y(z)

(z 1)(z2 5z 6)

(z 1)(z 2)(z 3)

Функция Y(z) представляет собой несократимую дробь, знаменатель ко-

торой имеет простые корни z1 1, z2 2, z3 3. Тогда по формуле (4.3) находим

y(n) ResY(z)zn 1 ResY(z)zn 1 ResY(z)zn 1			1	3 2n	5	3n.
			2		2
z 1	z 2	z 3

Проверим, выполняются ли начальные условия

	1				5									1			15
	y(0)					3				1, y(1)						6					1.
	y(0)					3				1, y(1)						6			2		1.
	2				2									2					2
					1						n		5		n
Значит, функция y(n)								3 2						3			является решением исходной
Значит, функция y(n)								3 2					2	3			является решением исходной
задачи.					2								2
задачи.
Задача 5.1. Найти экстремальные кривые функционала
								2					2			2
				I	[y(x)]								2	y		2	(x)) dx
				I	[y(x)]					(y (x))				y			(x)) dx
									0
при условиях y(0) 0,					y( 2) 1.
Решение.							2F					2F							2F
		F					2F					2F							2F
Находим			2y,							0,					0,						2. Отсюда уравне-
Находим			2y,							0,					0,						2. Отсюда уравне-
		y					x y					y y								2
																		y

ние Эйлера в данном конкретном случае будет иметь вид y	y 0. Экстре-
мальные кривые y(x) c1 sinx c2 cosx, а решение нашей задачи	y(x) sin x.

Задача 5.2. Найти экстремальные кривые, соответствующие минимальной длине кривой.

Решение.

I [y(x)]

1 y 2(x)dx при условиях y(x0) y0,

y(x1) y1.

x y

y y

y 2(x)

y 2

1 y 2(x)

(1 y 2(x))3

Уравнение Эйлера

0 y c1x c2. Учитывая граничные

y (x)

y 2

условия, найдем c , c

;

x1y0

x0 y1

Задача 5.3. Найти экстремальную кривую, соответствующую минимальной площади поверхности вращения.

(x1 y1)

(x2 y2 )

Решение.

S[y(x)] 2 y(x) 1 y 2(x) dx.

Так как F F(y, y ),

уравнение Эйлера имеет вид

y 0.

y y

y 2

Если уравнение Эйлера умножить на y

, получим

F y

Это уравнение имеет первый интеграл

F y

C1 y

1 y 2

C1.

1 y 2

Подстановка y ch t

дает

y C ch t dx

C {x C t C

, y C ch t}.

x C2

Или после исключения

уравнение цепной линии y C ch

Задача 6. Найти решение u(x,t) уравнения

0, 0 x 5, t 0,

с граничными условиями u(0, t) u(5, t) 0 и начальными условиями

u (x, 0) 25sin (4 x),

u(x, 0)

Реше ние.
В нашем случае a 7,l 5, (x) 25sin(4 x),	(x) 0,	x [0,5].

Решение данной краевой задачи определяется рядом (6.35), в котором коэффи-

циенты An, Bn, n N, вычисляются по формулам (6.38).

Так как (x) 0, x [0,5], то Bn 0,

n N . Определим теперь An.

2 l

2 5

(x) sin

d x

25sin(4 x) sin

x dx

l 0

20 n

25,

если n 20,

cos

если n 20.

Отсюда, учитывая формулу (6.35), решение искомой краевой задачи имеет вид

u(x, t) 25cos(28 t) sin(4 x).

Литература

1.Бицадзе, А. В. Уравнения математической физики / А. В. Бицадзе. –

М. : Наука, 1976. – 296 с.

2.Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа : учеб. пособие для втузов / В. А. Болгов [и др.] ; под общ. ред. А. В. Ефимова и Б. П. Демидовича – 2-е изд. – М. : Наука, 1986. – 368 с.

3.Гельфанд, И. М. Вариационное исчисление / И. М. Гельфанд, С. В. Фо-

мин. – М. : Наука, 1961. – 228 с.

4.Жевняк, Р. М. Высшая математика : Дифференциальные уравнения. Уравнения математической физики. Теория функций комплексной переменной : учеб. пособие / Р. М. Жевняк, А. А. Карпук. – Минск : ИРФ Обозрение, 1977. – 570 с.

5.Жевняк, Р. М. Высшая математика : Операционное исчисление. Теория вероятностей. Математическая статистика. Случайные процессы : учеб. пособие / Р. М. Жевняк, А. А. Карпук. – Минск : ИРФ Обозрение, 1977. – 445с.

6.Жевняк, Р. М. Высшая математика. В 10 ч. Ч. 5 : учеб. пособие / Р. М. Жевняк, А. А. Карпук. – Минск : Выш. шк., 1988. – 254 с.

7.Кофман, А. Введение в прикладную комбинаторику /А. Кофман. – М. :

Наука, 1975. – 368 с.

8.Краснов, М. Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости: учеб. пособие / М. Л. Краснов, А. И. Киселев, Г. И. Макаренко. – 2-е изд., перераб. и доп. – М. : Наука, 1991. – 304 с.

9.Краснов, М. Л. Интегральные уравнения. Серия «Избранные главы высшей математики для инженеров и студентов втузов». Задачи и упражнения / М. Л. Краснов, А. И. Киселев, Г. И. Макаренко. – М. : Наука, 1968. – 192 с.

10.Краснов, М. Л. Интегральные уравнения (Введение в теорию) /

М. Л. Краснов. – М. : Наука, 1975. – 304 с.

11.Михлин, С. Г. Лекции по линейным интегральным уравнениям : учеб. пособие / С. Г. Михлин. – М. : Наука, 1959. – 232 с.

12.Петровский, И. Г. Лекции об уравнениях с частными производными / И. Г. Петровский. – М. : Физматгиз, 1961. – 400 с.

13.Смирнов, М. М. Дифференциальные уравнения в частных производных второго порядка / М. М. Смирнов. – М. : Наука, 1964. – 208 с.

14.Тихонов, А. Н. Уравнения математической физики / А. Н. Тихонов, А. А. Самарский. – М. : Наука, 1977. – 736 с.

Контрольная работа

Вариант 1

1. Построить ортонормированный базис в R3 по данному базису. Доказать, что полученная система векторов является ортонормированной:

x1 ( 1, 1,1),

x2 2,

2,1 ,

x3 (0, 2,1).

2. Найти прямое преобразование Фурье функции

| x | 1,

(x)

| x | 1.

3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

полученного интеграла

n 1 xn

Решить линейное разностное уравнение

x(n 3) 3x (n 2) 3x (n 1) x(n) 2n,

x(0)

0, x(1) 0, x(2) 1.

Найти допустимые экстремали функционала

J(y) (12xy yy' (y')2) dx, y(0) 1, y(1)

Найти решение

u(x,t) уравнения

0, 0 x 1, t 0

с граничными условиями u(0, t) 0,u(1, t) 0 и начальными условиями

u(x,0) 2sin x,

u(x,0)

Вариант 2

x1 (1, 2,1),

x2 1, 3, 0 ,

x3 (1, 2, 1).

2. Найти прямое преобразование Фурье функции


sign x,		\| x \| 1,
f (x)	\| x\| 1.
0,	\| x\| 1.

3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

	xpe xq dx.
полученного интеграла

4. Решить линейное разностное уравнение

x(n 2) x(n 1) x(n) 0, x(0) 0, x(1) 1.

5. Найти допустимые экстремали функционала

1
J(y) (y 2xy' (y')2) dx,				y(0) 0,				y(1) 0.
0				2u			2u
6. Найти решение u(x,t) уравнения				2u			2u
					4			0 с граничными ус-
					4			0 с граничными ус-
				t2		x2
ловиями u(0,t) 0,u(2,t) 0 и начальными условиями
u (x, 0) 4sin	x		u(x,0)
		,				0.
	2	,		t		0.
	2			t

Вариант 3

1. Построить ортонормированный базис в R3 по данному базису. Доказать, что полученная система векторов является ортонормированной

x1 (5,1,1),

x2 0, 3,1 ,

x3 ( 2, 1, 1).

2. Найти прямое преобразование Фурье функции

f(x) e x, x 0, 0; f ( x) f (x).

3.Введя замену, свести данный интеграл к эйлерову. Вычислить значение

		(ln x)p	dx
полученного интеграла			dx	.
полученного интеграла				.
4.	1		x2
4.	Решить линейное разностное уравнение
5.	x(n 2) 3x(n 1) 10x(n) 0, x(0)						3, x(1) 1.
5.	Найти допустимые экстремали функционала							15
	2	2	2x					15
	ln2
	J(y) ((y )	3y ) e dx,			y(0) 0,			y(ln2)		.
	J(y) ((y )	3y ) e dx,			y(0) 0,			y(ln2)		.
	0							8
	Найти решение u(x,t) уравнения				2u		2u
6.						9			0 с граничными усло-
6.						9			0 с граничными усло-
					t2		x2

виями u(0,t) 0,u(3,t) 0 и начальными условиями

u(x,0) 5sin x, u(x,0) 0. 3 t

Вариант 4

x1 (1,1, 1),

x2 2,1, 1 ,

x3 (3, 0, 3).

2. Найти прямое преобразование Фурье функции

f (x) e

x 0, a 0,

x 0.

Введя замену, свести данный интеграл к эйлерову. Вычислить значение

xp 1

полученного интеграла

dx.

1 xq

Решить линейное разностное уравнение

x(n 2) 4x(n) 4n, x(0) 1, x(1)

Найти допустимые экстремали функционала

J(y) x2(y')2dx,

y(0) 3,

y(1) 1.

Найти решение u(x,t) уравнения

0 с граничными

условиями u(0,t) 0,u(4,t) 0 и начальными условиями

u(x,0) 6sin

u(x,0)

Вариант 5

x1 2,1, 1 ,

x2 ( 2,1,1),

x3 (0, 4, 2).

2, 0 x 3,

2. Найти прямое преобразование Фурье функции f (x)

0, x 0, x 3.

3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

1		x3
полученного интеграла			dx.


0	3 1 x3

4.	Решить линейное разностное уравнение
5.	x(n 2) 2x(n 1) x(n) ( 1)n, x(0)						0, x(1) 1.
5.	Найти допустимые экстремали функционала
	6	2
		2	)dx,	y(0) 1,			y(6) 1.
	J(y) (2xy (y )		)dx,	y(0) 1,			y(6) 1.
	0				2u			2u
	Найти решение u(x, t) уравнения				2u			2u
6.						25			0 с граничными
6.					t2	25		x2	0 с граничными

условиями u(0,t) 0, u(5, t) 0 и начальными условиями

x u(x,0)

u(x,0) 3sin		,		0.

5 t

Вариант 6

x1 3, 4, 5 ,

x2 ( 2, 1, 3),

x3 (0, 4, 1).

2. Найти прямое преобразование Фурье функции

1, 0 x 1,

f (x)

0, x 0,x 1.

3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

полученного интеграла x3 31 x3 dx.

4. Решить линейное разностное уравнение

x(n 2) x(n) ( 1)n, x(0) 1, x(1)

5. Найти допустимые экстремали функционала

ln2

J(y) ((y )

3y )e

dx,

y(0)

y(ln2)

6. Найти решение u(x,t) уравнения

0 с граничными усло-

виями u(0,t) 0,

u(1,t) 0 и начальными условиями

u(x,0) 4sin2 x,

u(x, 0)

Вариант 7

x1 3, 3, 4 ,

x2 ( 1, 1, 1),

x3 (0, 2,1).

2. Найти прямое преобразование Фурье функции

1,	\| x \| 2,
f (x)	\| x \| 2.
0,	\| x \| 2.

3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

a
a
полученного интеграла x2	a2 x2 dx	(a 0).
0

4. Решить линейное разностное уравнение

x(n 2) x(n) 1,x(0) 0,x(1) 1.

Найти допустимые экстремали функционала

) dx,

y(0) 0,

y(1) 0.

J(y) ((y )

6(y )

Найти решение u(x,t) уравнения

0 с граничными ус-

ловиями u(0,t) 0, u(2,t) 0 и начальными условиями

u(x, 0) 3sin x,

u(x, 0)

Вариант 8

Построить ортонормированный базис в R3

по данному базису. Дока-

зать, что полученная система векторов является ортонормированной:

x1 2, 2, 3 , x2

(3, 3, 0),

x3 (2,1, 0).

2 x 0,

Найти прямое преобразование Фурье функции

(x)

x 2,x 0.

Введя замену, свести данный интеграл к эйлерову. Вычислить значение

dx.

полученного интеграла

(1 x3)2

Решить линейное разностное уравнение

x(n 2) x(n) 1, x(0)

0,x(1) 0.

Найти допустимые экстремали функционала

) dx,

y(0) y( ) 0.

J(y) (4ycosx (y )

Найти решение u(x,t) уравнения

0 с граничными ус-

ловиями u(0,t) 0,u(3,t) 0

и начальными условиями

u(x,0) 2sin

2 x

u(x,0)

Вариант 9

x1 ( 1,1,1),

x2 2,1, 1 ,

x3 ( 2, 0, 2).

2. Найти прямое преобразование Фурье функции

		1,		\| x \| 3,
		f (x)		\| x \| 3.
3.		0,		\| x \| 3.
3.	Введя замену, свести данный интеграл к эйлерову. Вычислить значение

полученного интеграла		x6e x2 dx.
4.		0
4.	Решить линейное разностное уравнение
5.	x(n 2) 5x(n 1) 6x(n) 0, x(0) 1, x(1)									2.
5.	Найти допустимые экстремали функционала
	1
	J(y) (еx y y sin x)dx,					y(0)	2,		y(1) 0.
	0					2u			2u
6.	Найти решение u(x,t) уравнения					2u	16		2u	0 с граничными
6.	Найти решение u(x,t) уравнения					t2	16		x2	0 с граничными
условиями u(0,t) 0,		u (4, t) 0 и начальными условиями
		u(x,0) 5sin	x		u(x,0)
								0.
						t		0.
		2				t

Вариант 10

x1 (1,1,1),	x2 (1, 2, 1),	x3 (2, 1,1).
2. Найти прямое преобразование Фурье функции

1,	0 x 5,
f (x)	x 0,x 5.
0,
3. Введя замену, свести данный интеграл к эйлерову. Вычислить значение

1 x

полученного интеграла

0 3

(x 2)2

4. Решить линейное разностное уравнение

x(n 2) 6x(n 1) 13 x(n) 1, x(0)

0, x(1)

5. Найти допустимые экстремали функционала

J(y)

((y )

4y ) dx,

y(0) 0,

6. Найти решение u(x,t) уравнения

0 с граничными

условиями u(0,t) 0, u(5, t) 0 и начальными условиями

u(x, 0) 6sin

2 x

u(x, 0)

0 .

Св. план 2011, поз. 61

Учебное издание

Цегельник Владимир Владимирович Четыркина Зинаида Никандровна Ранцевич Валентина Алексеевна и др.

СПЕЦИАЛЬНЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ФУНКЦИИ

Методическое пособие для студентов специальностей 1-45 01 01 «Многоканальные системы телеком-

муникаций», 1-45 01 02 «Системы радиосвязи, радиовещания

ителевидения», 1-53 01 07 «Информационные технологии и управление

втехнических системах» заочной формы обучения

Редактор Т. П. Андрейченко

Корректор И. П. Острикова

Компьютерная верстка А. В. Бас

Подписано в печать 10.11.11.	Формат 60×84 1/16.	Бумага офсетная.
Гарнитура «Таймс».	Отпечатано на ризографе.	Усл. печ. л. 4,53.
Уч.-изд. л. 4,5.	Тираж 200 экз.	Заказ 875.

Издатель и полиграфическое исполнение: учреждение образования «Белорусский государственный университет информатики и радиоэлектроники»

ЛИ № 02330/0494371 от 16.03.2009. ЛП № 02330/0494175 от 03.04.2009. 220013, Минск, П. Бровки, 6

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.05.20151.62 Mб25методичка часть2.doc
#
11.05.2015145.41 Кб65Методичка ЭКЗАМ.Вус 404 2011 студенты.doc
#
01.05.202592.62 Кб0методичка эл тех материалы МиЭ-5з.docx
#
01.03.20251.01 Mб0Методичка №2 для кр №2(2008г) .doc
#
22.04.20192.7 Mб6Методичка(Денис)т13 для приложений и игр.doc
#
11.05.20154.86 Mб222методичка.pdf
#
11.05.20151.24 Mб36Методичка_2_семестр2007.doc
#
01.03.20251.39 Mб0Методичка_Дипломное проектирование.doc
#
01.04.2025792.06 Кб0Методуказания по дипломному проектированию.doc
#
27.09.2019109.57 Кб69Методы получения тонких пленок.doc
#
27.09.20198.22 Mб32Методы_и_устр_формир_и_обраб_телеком_сигналов_М...doc