Задача №1.5

Подбрасываются две игральные кости. Определить вероятность того, что выпадут разные, но четные числа.

Решение

Событие А состоит в том, что выпадут разные, но четные числа. Так как каждая игральная кость имеет 6 различных цифр от 1 до 6, то число все возможных исходов n опыта равно числу размещений с повторением элементов из 6 по 2 :

В наборе цифр игральной кости содержится 3 чётные цифры. Следовательно, число благоприятствующих исходов m опыта будет равно числу размещений без повторений элементов из 3 по 2:

Вероятность, того что выпадут разные, но четные числа:

Ответ:

Задача № 2.9

Дана схема соединения элементов, образующих цепь с одним входом и одним выходом (рисунок 2). Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

Рисунок 1

Решение

Согласно рисунку 1 схема состоит из двух участков. 1-ый участок содержит элементы 1 и 2, соединенные последовательно, 2-ой участок содержит элементы 3 и 4, соединенные последовательно. Участок 1 соединен параллельно с участком 2.

Введем события: A­₁ – элемент 1 исправен, A­₂ – элемент 2 исправен, A­₃ – элемент 3 исправен, A­₄ – элемент 4 исправен, A­₅ – элемент 5 исправен, A – исправен 1-ой участок схемы , B – исправен 2-ой участок схемы, С – сигнал проходит от точки a к точке b (со входа на выход).

Событие A произойдёт, если будут работать и элемент 1, и элемент 2:

_{Вероятность наступления события А:}

Событие B произойдёт, если будут работать и элемент 3, и элемент 4:

_{Вероятность наступления события B:}

Событие C произойдёт, если будут работать или 1 участок, или 2 участок схемы:

_{Вероятность наступления события С (сигнал пройдёт со входа на выход):}

Ответ:

Задача №3.16

Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. Определить вероятность того, что откажет один блок.

Решение

Событие А состоит в том, что откажет один блок. Введем события B₁ – 1-ый блок исправен, B₂ – 2-ой блок исправен, B₃ – 3-ий блок исправен.

Сделаем следующие предположения:

- отказал 1-ый блок:

- отказал 2-ой блок:

- отказал 3-ий блок:

Событие достоверно при всех вышеперечисленных гипотезах, следовательно, соответствующие условные вероятности равны единице:

Оставшиеся гипотезы можно не рассматривать, так как при них событие А никогда не произойдёт.

По формуле полной вероятности, вероятность того, что откажет один блок:

Ответ:

Задача №4.27

Вероятность того, что данный баскетболист забросит мяч в корзину, равна 0,95. Произведено десять бросков. Найти вероятность того, что будет девять попаданий.

Решение

Вероятность того, что из n=10 бросков в корзину k=9 окажутся удачными, определим по формуле Бернулли:

Ответ:

Задача № 5.7

Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

Таблица 1 – Исходные данные

	-5	-2	0	1	2
	0,5	0,1	0,1	0,2	0,1

Решение

1. Математическое ожидание и дисперсию величины Х:

2. Построим ряд распределения СВ X:

Таблица 2 –Ряд распределения СВ X

	-5	-2	0	1	2	>2
	0,5	0,1	0,1	0,2	0,1	0
	0	0,5	0,6	0,7	0,9	1

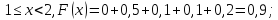
Построим график функции распределения (рисунок 2):

Рисунок 2 - график функции распределения F(X­_i)

Задача № 6.22

Случайная величина Х задана плотностью вероятности:

Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал.

Решение

1. Вычислим константу исходя из условия нормировки:

Отсюда константа :

2. Определим математическое ожидание СВ Х:

3. Определим дисперсию СВ Х:

4. Определим функцию распределения величины Х:

5. Определим вероятность попадания величины Х в заданный интервал :

Ответ:

Задача № 7.20

Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).

Решение

1. Построим график случайной величины для в интервале значений и определим диапазон значений (Рисунок 3): [1; 7,389]

2. В зависимости от числа обратных функций выделим следующие интервалы для :

обратных функций не существует

обратных функций не существует

3. Вычислим модули производных обратных функций:

Y

X

Рисунок 3 – график функции

Так как случайная величина Х распределена равномерно на интервале [-1;2] , то её плотность вероятности равна:

4. Определим плотность вероятности величины :

Задача № 8.10

Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями (рисунок 4) области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

Таблица 3 – Исходные данные

Вариант	x1	x2	x3	x4	x5	x6	y1	y2
8.10	0	0	4	4	2	2	1	2

Рисунок 4

Решение

1. Построим область B согласно координатам из таблицы 3 и рисунку 4.

Рисунок 5

Проанализируем рисунок 5: область B на промежутке ограничена сверху прямой , снизу ; на промежутке ограничена сверху прямой , снизу ;

Следовательно, совместная плотность вероятности примет вид:

2. Найдём константу из условия нормировки:

Таким образом:

Проверим полученный результат геометрически. Объём тела, ограниченного поверхностью распределения В и плоскостью xOy равен 1, т.е:

Следовательно, константа рассчитана верно.

3. Вычислим математические ожидания:

4. Вычислим дисперсии:

Вычислим корреляционный момент:

5. Вычислим коэффициент корреляции между величинами X и Y:

_Ответ:

Задача № 9

По выборке одномерной случайной величины:

- получить вариационный ряд;

- построить график эмпирической функции распределения F^*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить точечные оценки математического ожидания и дисперсии;

- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);

- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия ² и критерия Колмогорова ( = 0,05).

Одномерная выборка:

_Размер выборки

2,18	1,12	1,49	0,28	4,25	0,32	6,38	0,06	0,49	2,09	1,70	0,43	0,50	4,84	2,39
0,57	2,55	3,24	4,15	2,33	3,90	2,94	0,63	0,05	0,13	3,82	1,27	4,60	0,91	2,43
3,36	1,88	4,32	8,21	4,29	0,84	6,41	4,54	2,37	0,37	3,86	0,35	2,10	4,64	3,20
0,30	1,77	7,64	0,98	3,55	0,54	6,45	0,47	1,55	7,65	6,34	0,44	0,16	2,77	0,69
0,58	1,23	0,87	0,62	0,04	0,29	4,69	2,41	0,10	7,35	2,51	2,13	0,91	9,27	4,44
1,62	1,13	1,39	5,34	1,89	0,47	1,62	1,52	0,25	0,98	1,96	1,61	0,91	0,12	4,38
0,25	2,60	4,02	1,51	0,05	2,20	3,06	0,08	4,38	1,70