
Решение
-
Получим вариационный ряд из исходного:
|
-8,39 |
-8,27 |
-8,15 |
-8,12 |
-8,10 |
-8,10 |
-8,03 |
-7,95 |
-7,85 |
-7,82 |
-7,69 |
-7,60 |
-7,55 |
-7,47 |
-7,41 |
|
-7,38 |
-7,37 |
-7,37 |
-7,35 |
-7,32 |
-7,28 |
-7,23 |
-7,22 |
-7,12 |
-7,06 |
-6,89 |
-6,84 |
-6,81 |
-6,81 |
-6,73 |
|
-6,67 |
-6,64 |
-6,61 |
-6,60 |
-6,60 |
-6,38 |
-6,22 |
-6,20 |
-6,12 |
-6,02 |
-5,84 |
-5,77 |
-5,72 |
-5,68 |
-5,62 |
|
-5,61 |
-5,59 |
-5,58 |
-5,57 |
-5,56 |
-5,49 |
-5,48 |
-5,44 |
-5,43 |
-5,21 |
-5,20 |
-5,19 |
-5,15 |
-5,14 |
-5,11 |
|
-5,10 |
-5,07 |
-5,07 |
-4,98 |
-4,96 |
-4,84 |
-4,76 |
-4,75 |
-4,69 |
-4,68 |
-4,62 |
-4,47 |
-4,44 |
-4,43 |
-4,39 |
|
-4,37 |
-4,35 |
-4,28 |
-4,23 |
-4,16 |
-4,15 |
-4,07 |
-4,03 |
-3,97 |
-3,86 |
-3,75 |
-3,71 |
-3,68 |
-3,66 |
-3,65 |
|
-3,52 |
-3,50 |
-3,42 |
-3,41 |
-3,34 |
-3,12 |
-2,88 |
-2,77 |
-2,65 |
-2,65 |
|
|
|
|
|
2)
Построим график эмпирической функции
непосредственно по вариационному ряду,
так как F*(x)
– неубывающая и практически все ступеньки
графика имеют одинаковую величину
 (Рисунок 6).
(Рисунок 6).
-
Построим гистограмму равноинтервальным способом (рисунок 7).
Для построения гистограммы составим интервальный статистический ряд, учитывая что длина у всех интервалов должна быть одинаковая.
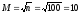 -
количество интервалов;
-
количество интервалов;
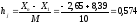 -
ширина интервала;
-
ширина интервала;
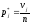 -
частота попадания СВ X
в j-ый
интервал;
-
частота попадания СВ X
в j-ый
интервал;
 -
статистическая плотность в j-ом
интервале.
-
статистическая плотность в j-ом
интервале.
Таблица 4 – Интервальный статистический ряд
|
j |
Aj |
Bj |
hj |
vj |
pj* |
fj* |
|
1 |
-8,39 |
-7,816 |
0,574 |
10 |
0,1 |
0,174 |
|
2 |
-7,816 |
-7,242 |
0,574 |
11 |
0,11 |
0,192 |
|
3 |
-7,242 |
-6,668 |
0,574 |
10 |
0,1 |
0,174 |
|
4 |
-6,668 |
-6,094 |
0,574 |
8 |
0,08 |
0,139 |
|
5 |
-6,094 |
-5,52 |
0,574 |
11 |
0,11 |
0,192 |
|
6 |
-5,52 |
-4,946 |
0,574 |
15 |
0,15 |
0,261 |
|
7 |
-4,946 |
-4,372 |
0,574 |
10 |
0,1 |
0,174 |
|
8 |
-4,372 |
-3,798 |
0,574 |
10 |
0,1 |
0,174 |
|
9 |
-3,798 |
-3,224 |
0,574 |
10 |
0,1 |
0,174 |
|
10 |
-3,224 |
-2,65 |
0,574 |
5 |
0,05 |
0,087 |
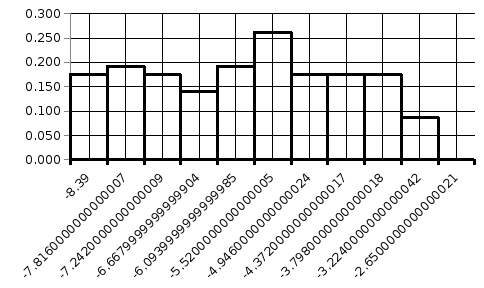
X
f*(x)
Рисунок 7
-
Построим гистограмму равновероятностным способом (рисунок 8).
Для построения гистограммы составим интервальный статистический ряд, учитывая что частота попадания СВ X в в каждый j-ый интервал должна быть одинаковая (Таблица 5).
Таблица 5 – Интервальный статистический ряд
|
j |
Aj |
Bj |
hj |
vj |
pj* |
fj* |
|
1 |
-8,39 |
-7,755 |
0,635 |
10 |
0,1 |
0,157 |
|
2 |
-7,755 |
-7,3 |
0,455 |
10 |
0,1 |
0,220 |
|
3 |
-7,3 |
-6,7 |
0,6 |
10 |
0,1 |
0,167 |
|
4 |
-6,7 |
-5,93 |
0,77 |
10 |
0,1 |
0,130 |
|
5 |
-5,93 |
-5,525 |
0,405 |
10 |
0,1 |
0,247 |
|
6 |
-5,525 |
-5,105 |
0,42 |
10 |
0,1 |
0,238 |
|
7 |
-5,105 |
-4,65 |
0,455 |
10 |
0,1 |
0,220 |
|
8 |
-4,65 |
-4,155 |
0,495 |
10 |
0,1 |
0,202 |
|
9 |
-4,155 |
-3,585 |
0,57 |
10 |
0,1 |
0,175 |
|
10 |
-3,585 |
-2,65 |
0,935 |
10 |
0,1 |
0,107 |

f*(x)
X
Рисунок 8
-
Вычислим точечные оценки математического ожидания и дисперсии:


-
Вычислим интервальные оценки математического ожидания и дисперсии (γ = 0,95):





-
По виду графика эмпирической функции распределения
 и
гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения
случайной величины X:
и
гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения
случайной величины X:
H0 – величина X распределена по равномерному закону:
 -
параметры
распределения
-
параметры
распределения
H1 – величина X не распределена по равномерному закону:

Проверим
гипотезу о равномерном законе по критерию
Пирсона
 .
Вычислим значение критерия
.
Вычислим значение критерия
 на основе равноинтервального
статистического ряда:
на основе равноинтервального
статистического ряда:

Теоретические вероятности попадания в интервалы вычислим по формуле:

Таблица 6 – Результаты расчётов
|
|
|
|
|
|
|
|||
|
1 |
-8,39 |
-7,816 |
0,100 |
0,100 |
0,000 |
|||
|
2 |
-7,816 |
-7,242 |
0,100 |
0,110 |
0,001 |
|||
|
3 |
-7,242 |
-6,668 |
0,100 |
0,100 |
0,000 |
|||
|
4 |
-6,668 |
-6,094 |
0,100 |
0,080 |
0,004 |
|||
|
5 |
-6,094 |
-5,52 |
0,100 |
0,110 |
0,001 |
|||
|
6 |
-5,52 |
-4,946 |
0,100 |
0,150 |
0,025 |
|||
|
7 |
-4,946 |
-4,372 |
0,100 |
0,100 |
0,000 |
|||
|
8 |
-4,372 |
-3,798 |
0,100 |
0,100 |
0,000 |
|||
|
9 |
-3,798 |
-3,224 |
0,100 |
0,100 |
0,000 |
|||
|
10 |
-3,224 |
-2,65 |
0,100 |
0,050 |
0,025 |
|||
|
Сумма:
|
1,000 |
1,000 |
0,056 |
|||||
Проверим
правильность вычислений
 :
:
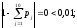
Вычислим критерий Пирсона:
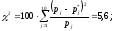
Определим число степеней свободы:

Выбираем
критическое значения критерия Пирсона
из таблицы [1, стр.63] для степени свободы
 и
заданного уровня значимости
и
заданного уровня значимости
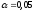 :
:

Так как условие выполняется, то гипотеза H0 о равномерном законе распределения принимается (нет оснований ее отклонить).
8)
Проверим гипотезу при помощи критерия
Колмогорова. Для этого построим график
гипотетической функции распределения
 в
одной системе координат с эмпирической
функцией
в
одной системе координат с эмпирической
функцией
 (рисунок
6). В качестве опорных точек используем
10 значений
(рисунок
6). В качестве опорных точек используем
10 значений
 из
таблицы 6. По графику определим максимальное
по модулю отклонение между функциями
из
таблицы 6. По графику определим максимальное
по модулю отклонение между функциями
 и
и
 :
:

Вычислим значение критерия Колмогорова:
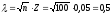
Из
таблицы Колмогорова [1, стр. 64] по заданному
уровню значимости
 выбираем
критическое значение критерия:
выбираем
критическое значение критерия:

Так как условие выполняется, гипотеза H0 о равномерном законе распределения принимается (нет оснований ее отклонить).






