Задача №10

По выборке двухмерной случайной величины:

- вычислить точечную оценку коэффициента корреляции;

- вычислить интервальную оценку коэффициента корреляции ;

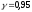- проверить гипотезу об отсутствии корреляционной зависимости ;

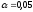- вычислить оценки параметров a₀ и a₁ линии регрессии ;

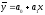- построить диаграмму рассеивания и линию регрессии.

Выборка:

( 4.95; -0.88) ( 3.25; -2.54) ( 2.28; -0.00) ( 1.17; 3.16) ( -2.13; 3.37) ( 3.87; -0.35) ( 2.35; -1.99) ( 2.90; -1.88)

( 1.47; -0.26) ( 4.25; -2.19) ( 2.77; 1.24) ( 3.91; -3.37) ( 1.55; 1.05) ( 2.71; -0.41) ( 4.22; -3.99) ( 4.31; -2.31)

( 3.25; -1.37) ( 3.15; 0.51) ( 2.44; 0.25) ( 0.68; 2.04) ( 1.41; 0.70) ( 4.51; -2.51) ( 3.30; -0.29) ( 1.43; -0.04)

( 1.08; -0.25) ( 3.83; -2.02) ( 4.32; -1.90) ( -0.74; 0.65) ( 1.45; -0.21) ( 0.86; 1.22) ( 2.48; -1.86) ( 4.84; -0.45)

( 4.54; -4.16) ( 1.62; -0.91) ( -2.22; 2.93) ( 3.85; -2.36) ( 1.25; 0.86) ( 2.91; 0.34) ( 3.67; -1.81) ( 1.50; -1.53)

( 0.91; 0.47) ( 1.95; -0.81) ( 1.29; -1.64) ( 2.96; -2.92) ( 3.59; -2.29) ( 0.92; -0.09) ( 0.04; 0.98) ( 3.24; -2.09)

( 0.44; 1.91) ( 2.57; -0.43)

Решение

Для удобства все промежуточные вычисления поместим в таблицу 7, Вычислим:

1. Оценки математических ожиданий по каждой переменной:

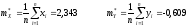
2. Оценки начальных моментов второго порядка по каждой переменной:

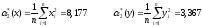
3. Оценку смешанного начального момента второго порядка:

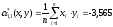
4. Оценки дисперсий:

5. Оценку корреляционного момента:

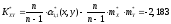
Таблица 7 – Результаты промежуточных вычислений

	x	y	x2	y2­	x*y
	4,950	-0,880	24,503	0,774	-4,356
	3,250	-2,540	10,563	6,452	-8,255
	2,280	0,000	5,198	0,000	0,000
	1,170	3,160	1,369	9,986	3,697
	-2,130	3,370	4,537	11,357	-7,178
	3,870	-0,350	14,977	0,123	-1,355
	2,350	-1,990	5,523	3,960	-4,677
	2,900	-1,880	8,410	3,534	-5,452
	1,470	-0,260	2,161	0,068	-0,382
	4,250	-2,190	18,063	4,796	-9,308
	2,770	1,240	7,673	1,538	3,435
	3,910	-3,370	15,288	11,357	-13,177
	1,550	1,050	2,403	1,103	1,628
	2,710	-0,410	7,344	0,168	-1,111
	4,220	-3,990	17,808	15,920	-16,838
	4,310	-2,310	18,576	5,336	-9,956
	3,250	-1,370	10,563	1,877	-4,453
	3,150	0,510	9,923	0,260	1,607
	2,440	0,250	5,954	0,063	0,610
	0,680	2,040	0,462	4,162	1,387
	1,410	0,700	1,988	0,490	0,987
	4,510	-2,510	20,340	6,300	-11,320
	3,300	-0,290	10,890	0,084	-0,957
	1,430	-0,040	2,045	0,002	-0,057
	1,080	-0,250	1,166	0,063	-0,270
	3,830	-2,020	14,669	4,080	-7,737
	4,320	-1,900	18,662	3,610	-8,208
	-0,740	0,650	0,548	0,423	-0,481
	1,450	-0,210	2,103	0,044	-0,305
	0,860	1,220	0,740	1,488	1,049
	2,480	-1,860	6,150	3,460	-4,613
	4,840	-0,450	23,426	0,203	-2,178
	4,540	-4,160	20,612	17,306	-18,886
	1,620	-0,910	2,624	0,828	-1,474
	-2,220	2,930	4,928	8,585	-6,505
	3,850	-2,360	14,823	5,570	-9,086
	1,250	0,860	1,563	0,740	1,075
	2,910	0,340	8,468	0,116	0,989
	3,670	-1,810	13,469	3,276	-6,643
	1,500	-1,530	2,250	2,341	-2,295
	0,910	0,470	0,828	0,221	0,428
	1,950	-0,810	3,803	0,656	-1,580
	1,290	-1,640	1,664	2,690	-2,116
	2,960	-2,920	8,762	8,526	-8,643
	3,590	-2,290	12,888	5,244	-8,221
	0,920	-0,090	0,846	0,008	-0,083
	0,040	0,980	0,002	0,960	0,039
	3,240	-2,090	10,498	4,368	-6,772
	0,440	1,910	0,194	3,648	0,840
	2,570	-0,430	6,605	0,185	-1,105
Сумма:	117,15	-30,43	408,8465	168,345	-178,258

6. Точечную оценку коэффициента корреляции:

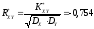
7. Вычислим интервальную оценку коэффициента корреляции с заданной надёжностью 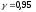, По таблице функции Лапласа [1, стр, 61] :

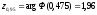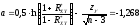
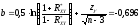
Таким образом, доверительный интервал для коэффициента корреляции имеет вид:

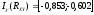
8. Проверим гипотезу о корреляционной зависимости:

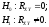
Так как объём выборки велик (n>50), то критерий вычислим по формуле:

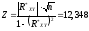
По таблице функции Лапласа .

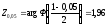Так как 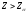, то гипотеза 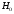отклоняется, т.е, величины 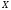и 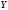коррелированны.

9. Вычислим оценки параметров линии регрессии:

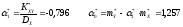
Уравнение линии регрессии имеет вид:

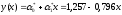
Исходя из двухмерной выборки построим диаграмму рассеивания и линию регрессии 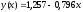(рисунок 10):

Список литературы

1. А, И, Волковец, А, Б, Гуринович, А, В,Аксенчик, Теория вероятностей и математическая статистика: метод, указания по типовому расчету ,– Минск БГУИР, 2009, – 65 с,: ил,

2. А, И, Волковец, А, Б, Гуринович, Теория вероятностей и математическая статистика: Конспект лекций для студ, всех спец, и форм обучения,– Минск БГУИР, 2003, – 84 л,