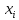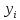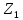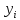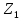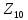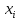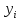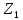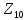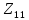Решение:

1. В качестве первого центра класса выберем элемент .

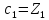2. В качестве второго центра класса выберем тот элемен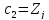т , который находится на наибольшем расстоянии от 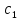, для этого вычислим расстояния от всех 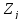до , будем использовать евклидову метрику.

Объекты			Расстояние до
Z1	4	1	С1
Z2	4	2	1,00
Z3	4	3	2,00
Z4	5	3	2,24
Z5	9	4	5,83
Z6	8	4	5,00
Z7	8	3	4,47
Z8	9	3	5,39
Z9	9	2	5,10
Z10	10	1	6,00
Z11	7	4	4,24
Z12	7	1	3,00

Из таблицы видно, что максимальное расстояние до точки 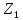имеет точка 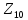, , 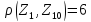значит вторым центром будет точка .

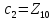Разобьем все точки на два класса по наименьшему расстоянию, получим

.

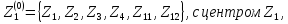
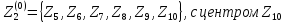Формула суммарной выборочной дисперсии разброса элементов относительно центров классов:

.

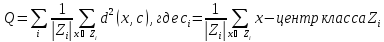По формуле посчитаем

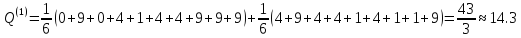
3. Найдем третий центр. В качестве выберем тот элемент , который находится на наибольшем расстоянии от ближайшего из центров.

Объекты			Расстояние до	Расстояние до	min
Z1	4	1	С1
Z2	4	2	1,00	6,08	1,00
Z3	4	3	2,00	6,32	2,00
Z4	5	3	2,24	5,39	2,24
Z5	9	4	5,83	3,16	3,16
Z6	8	4	5,00	3,61	3,61
Z7	8	3	4,47	2,83	2,83
Z8	9	3	5,39	2,24	2,24
Z9	9	2	5,10	1,41	1,41
Z10	10	1	С2
Z11	7	4	4,24	4,24	4,24
Z12	7	1	3,00	3,00	3,00

В колонке min находится минимальное значение расстояний от точек 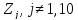до точек 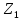,,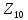 и затем выбираем из этой колонки максимальное расстояние – это 4,24 от точки 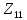до точки и до точки 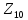, значит 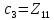. Распределим тачки по трем классам методом ближайшего расстояния.

Объекты			Расстояние до	Расстояние до	Расстояние до	min
Z1	4	1	С1
Z2	4	2	1,00	6,08	3,61	1,00
Z3	4	3	2,00	6,32	3,16	2,00
Z4	5	3	2,24	5,39	2,24	2,24
Z5	9	4	5,83	3,16	2,00	2,00
Z6	8	4	5,00	3,61	1,00	1,00
Z7	8	3	4,47	2,83	1,41	1,41
Z8	9	3	5,39	2,24	2,24	2,24
Z9	9	2	5,10	1,41	2,83	1,41
Z10	10	1	С2
Z11	7	4	С3
Z12	7	1	3,00	3,00	3,00	3,00

Получили

,

.

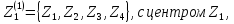
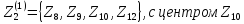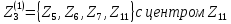Посчитаем суммарную выборочную дисперсию разброса элементов относительно центров классов:

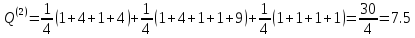
Так как 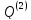значительно отличается от 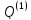, то продолжим алгоритм.