
- •Решение:
- •Классифицируемый объект а(7, 4)
- •Классифицируемый объект b(7, 1)
- •Итерация 2:
- •Итерация 3:
- •Решение:
- •Найдем третий центр. В качестве выберем тот элемент , который находится на наибольшем расстоянии от ближайшего из центров.
- •Из последней таблицы видно, что четвертым центром будет . Распределим точки по четырем классам:
- •Дополнительные советы по выполнению работы.
Задание 1. По обучающей выборке точек, распределенных по классам Со (С1 = 1 – 1-ый класс, С2 = 2 – 2-ой класс), определите принадлежность точек A и B одному из заданных классов.
Используйте
для этого алгоритм К-ближайших
представителей (К
положите
равным 3 и 5) и три типа метрик для
определения минимального расстояния:
евклидову, Чебышева, по Манхэттену.
Полученное решение оформите в виде
сводной таблицы для удобного сравнения
результатов по каждому параметру.
Сделайте чертеж.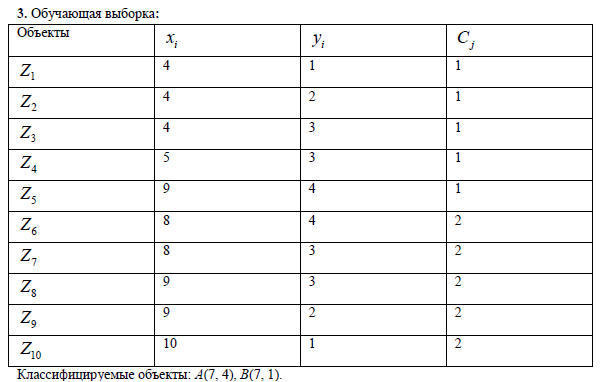
Решение:
Приведем
формулы нахождения расстояния
 между точками
между точками
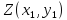 и
и
 :
:
Евклидов
метод
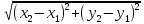
по
Манхэттену

метод
Чебышева
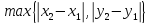
-
Классифицируемый объект а(7, 4)
Построим сводную таблицу. Расчеты в таблице получены по вышеуказанным формулам.
|
Zj |
Xj |
Yj |
Сj |
Евклид |
Манхэттен |
Чебышев |
|
Z1 |
4 |
1 |
1 |
4,2 |
6 |
3 |
|
Z2 |
4 |
2 |
1 |
3,6 |
5 |
3 |
|
Z3 |
4 |
3 |
1 |
3,2 |
5 |
3 |
|
Z4 |
5 |
3 |
1 |
2,2 |
3 |
2 |
|
Z5 |
9 |
4 |
1 |
2,0 |
2 |
2 |
|
Z6 |
8 |
4 |
2 |
1,0 |
1 |
1 |
|
Z7 |
8 |
3 |
2 |
1,4 |
2 |
1 |
|
Z8 |
9 |
3 |
2 |
2,2 |
3 |
2 |
|
Z9 |
9 |
2 |
2 |
2,8 |
4 |
2 |
|
Z10 |
10 |
1 |
2 |
4,2 |
6 |
3 |
Используя алгоритм К-ближайших представителей, выберем точки, ближайшие к точке А.
При
К=3
по
всем метрикам
ближайшими точками будут точки
 .
Две из них принадлежат 2 классу, значит
и точка А
будет принадлежать 2
классу.
.
Две из них принадлежат 2 классу, значит
и точка А
будет принадлежать 2
классу.
При
К=5
по
всем метрикам
ближайшими точками будут точки
 .
Три из них принадлежат 2 классу, значит
и точка А
будет принадлежать 2
классу.
.
Три из них принадлежат 2 классу, значит
и точка А
будет принадлежать 2
классу.
-
Классифицируемый объект b(7, 1)
Построим сводную таблицу. Расчеты в таблице получены по вышеуказанным формулам.
|
Zj |
Xj |
Yj |
Сj |
Евклид |
Манхэттен |
Чебышев |
|
Z1 |
4 |
1 |
1 |
3,0 |
3 |
3 |
|
Z2 |
4 |
2 |
1 |
3,2 |
4 |
3 |
|
Z3 |
4 |
3 |
1 |
3,6 |
5 |
3 |
|
Z4 |
5 |
3 |
1 |
2,8 |
4 |
2 |
|
Z5 |
9 |
4 |
1 |
3,6 |
5 |
3 |
|
Z6 |
8 |
4 |
2 |
3,2 |
4 |
3 |
|
Z7 |
8 |
3 |
2 |
2,2 |
3 |
2 |
|
Z8 |
9 |
3 |
2 |
2,8 |
4 |
2 |
|
Z9 |
9 |
2 |
2 |
2,2 |
3 |
2 |
|
Z10 |
10 |
1 |
2 |
3,0 |
3 |
3 |
Используя алгоритм К-ближайших представителей, выберем точки, ближайшие к точке А.
Положим
К=3,
тогда по
Эвклидовой
метрике
ближайшими точками будут точки
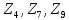 ,
две из них принадлежат 2
классу; по Манхеттену ближайшие
точки Z1,
Z7,
Z9,
две
из которых также принадлежат 2
классу;
по
Чебышеву
ближайшие точки Z4,
Z7,
Z8
две из которых также принадлежат 2
классу,
значит и точка В будет принадлежать 2
классу.
,
две из них принадлежат 2
классу; по Манхеттену ближайшие
точки Z1,
Z7,
Z9,
две
из которых также принадлежат 2
классу;
по
Чебышеву
ближайшие точки Z4,
Z7,
Z8
две из которых также принадлежат 2
классу,
значит и точка В будет принадлежать 2
классу.
Положим
К=5,
тогда по
Эвклидовой
метрике
ближайшими точками будут точки
 ,
три из них принадлежат 2
классу; по Манхеттену ближайшие
точки
,
три из них принадлежат 2
классу; по Манхеттену ближайшие
точки
 ,
три
из которых также принадлежат 2
классу;
по
Чебышеву
ближайшие точки
,
три
из которых также принадлежат 2
классу;
по
Чебышеву
ближайшие точки
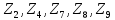 ,
три из которых также принадлежат 2
классу,
значит и точка В будет принадлежать 2
классу.
,
три из которых также принадлежат 2
классу,
значит и точка В будет принадлежать 2
классу.
Ответ: по алгоритму К-ближайших представителей при К=3 и К=5 по трем метрикам, точка В принадлежит 2 классу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Задание 2. Используя алгоритм К-средних (k-means), разбейте массив точек на 4 класса (К=4) и определите их центры. Проиллюстрируйте свое решение.

Решение:
Итерация 1:
В
качестве начальных центров классов
выберем точки
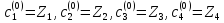 .
Разобьем
выборку по методу ближайшего соседа.
По методу Эвклида найдем расстояние
между центрами классов и остальными
точками:
.
Разобьем
выборку по методу ближайшего соседа.
По методу Эвклида найдем расстояние
между центрами классов и остальными
точками:
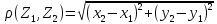
Составим сводную таблицу:
|
Объекты |
Xj |
Yj |
Расстояние до Z1 |
Расстояние до Z2 |
Расстояние до Z3 |
Расстояние до Z4 |
Класс |
|
● Z1 |
4 |
1 |
- |
- |
- |
- |
1 |
|
● Z2 |
4 |
2 |
- |
- |
- |
- |
2 |
|
● Z3 |
4 |
3 |
- |
- |
- |
- |
3 |
|
● Z4 |
5 |
3 |
- |
- |
- |
- |
4 |
|
Z5 |
9 |
4 |
5,83 |
5,39 |
5,10 |
4,12 |
4 |
|
Z6 |
8 |
4 |
5,00 |
4,47 |
4,12 |
3,16 |
4 |
|
Z7 |
8 |
3 |
4,47 |
4,12 |
4,00 |
3,00 |
4 |
|
Z8 |
9 |
3 |
5,39 |
5,10 |
5,00 |
4,00 |
4 |
|
Z9 |
9 |
2 |
5,10 |
5,00 |
5,10 |
4,12 |
4 |
|
Z10 |
10 |
1 |
6,00 |
6,08 |
6,32 |
5,39 |
4 |
|
Z11 |
7 |
4 |
4,24 |
3,61 |
3,16 |
2,24 |
4 |
|
Z12 |
7 |
1 |
3,00 |
3,16 |
3,61 |
2,83 |
4 |
Получим
начальные классы
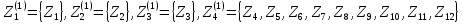 .
.
Вычислим новые центры – центры тяжести классов
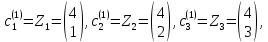


Сравниваем: .
.
Продолжаем выполнение алгоритма.

