- •2. Протокол udp
- •3. Протокол http. Общие сведения.
- •4.Протокол http. Методы запросов. Спецификация mime
- •1Xx Informational («Информационный»)
- •Операции фильтрации
- •6.Работа с документами xml
- •7.Почтовый протокол smtp.
- •8.Почтовый протокол pop3.
- •9.Понятие криптографии. Классификация алгоритмов шифрования.
- •10. Хэширование. Основные алгоритмы хэширования.
- •11. Симметричное шифрование. Основные алгоритмы симметричного шифрования
- •12.Асимметричное шифрование. Основные алгоритмы асимметричного шифрования. Описание алгоритма rsa
- •13. Электронная цифровая подпись.
- •14. Инфраструктура открытых ключей
- •15.Сертификаты X.509. Структура сертификата. Процедура проверки подлинности.
12.Асимметричное шифрование. Основные алгоритмы асимметричного шифрования. Описание алгоритма rsa
Асимметричные криптографические системы были разработаны в 1970-х годах. Принципиальное отличие асимметричной криптосистемы от криптосистемы симметричного шифрования состоит в том, что для шифрования информации и ее последующего расшифрования используются различные ключи:
открытый ключ K: используется для шифрования информации, вычисляется из секретного ключа k;
секретный ключ k: используется для расшифрования информации, зашифрованной с помощью парного ему открытого ключа K.
Эти ключи различаются таким образом, что с помощью вычислений нельзя вывести секретный ключ k из открытого ключа K. Поэтому открытый ключ K может свободно передаваться по каналам связи.
Асимметричные системы называют еще двухключевыми криптографическими системами или криптосистемами с открытым ключом.
Обобщенная схема асимметричной криптосистемы шифрования

Для криптографического закрытия и последующего расшифрования передаваемой информации используются открытый и секретный ключи получателя В сообщения. В качестве ключа зашифрования должен использоваться открытый ключ получателя, а в качестве ключа расшифрования – его секретный ключ.
Секретный и открытый ключи генерируются попарно. Секретный ключ должен оставаться у его владельца; он должен быть надежно защищен от несанкционированного доступа (аналогично ключу шифрования в симметричных алгоритмах). Копия открытого ключа должна иметься у каждого абонента криптографической сети, с которым обменивается информацией владелец секретного ключа.
Процесс шифрования и передачи сообщения
Процесс передачи зашифрованной информации в асимметричной криптосистеме осуществляется следующим образом:
1.Подготовительный этап.
Абонент В генерирует пару ключей: секретный ключ kB и открытый ключ Кв. Открытый ключ Кв посылается абоненту А и остальным абонентам (или делается доступным, например, на разделяемом ресурсе).
2.Использование - обмен информацией между абонентами А и В.
Абонент А зашифровывает сообщение с помощью открытого ключа КВ абонента В и отправляет шифротекст абоненту В. Абонент В расшифровывает сообщение с помощью своего секретного ключа kB. Никто другой (в том числе абонент А) не может расшифровать данное сообщение, так как не имеет секретного ключа абонента В. Защита информации в асимметричной криптосистеме основана на секретности ключа kB получателя сообщения
Односторонние функции
Асимметричные алгоритмы основаны на использовании односторонних функций.
Функция F:X→Y называется односторонней, если выполняются следующие два условия:
существует эффективный алгоритм, вычисляющий F(x) для любого x∈X;
не существует эффективного алгоритма инвертирования функции F, т.е. алгоритма, позволяющего определить значение x по значению F(x).
«Эффективным» называется полиномиальный алгоритм, т.е. алгоритм, который для получения результата для входа длины n тратит не более P(n) шагов, где P — некоторый полином.
Не любая односторонняя функция не может быть использована для шифрования. Действительно, если преобразовать открытый текст t с помощью односторонней функции: c = F(t), то расшифровать полученный текст, то есть по c восстановить t, не сможет уже никто, в том числе и законный получатель. Для использования в криптографии необходимо, чтобы задача инвертирования шифрующего преобразования (т.е. вычисления t по F(t)) была разрешима за приемлемое время, но сделать это мог только тот, кто знает секретный ключ. Такие функции называются односторонними функциями с секретом
Односторонняя функция с секретом — это функция Fk:X→Y, зависящая от параметра k∈K (этот параметр называется секретом), для которой выполняются следующие условия:
при любом k∈K существует эффективный алгоритм, вычисляющий Fk(x) для любого x∈X;
при неизвестном k не существует эффективного алгоритма инвертирования функции Fk;
при известном k существует эффективный алгоритм инвертирования функции Fk.
Алгоритм RSA
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом, так и закрытым ключом. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их.
Взаимно простыми числами называются такие числа, которые не имеют ни одного общего делителя, кроме 1.
Функция Эйлера (p) от натурального p есть количество чисел, меньших p и взаимно простых с n (число 1 взаимно просто с любым числом).
Если p — простое число, то (p) = p - 1.
Если p — простое, a — натуральное число, то (pa) = pa - pa-1 .
Если p и q взаимно простые, то (pq) =(p)(q)
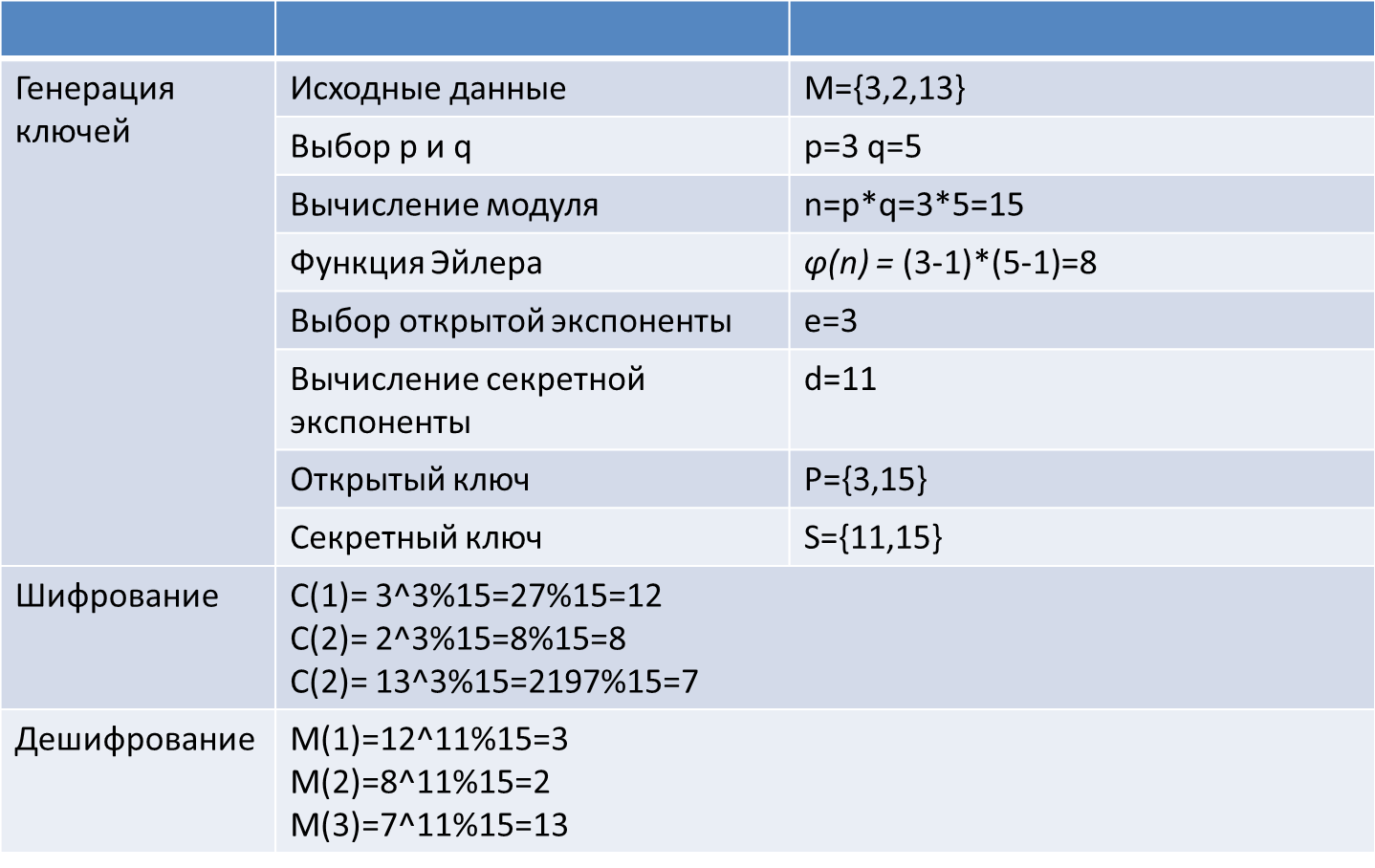
Генерация ключей выполняется по следующему алгоритму:
1. Выбираются два больших простых числа p, q (на сегодняшний день обычно выбирают числа, содержащие от 200 до 400 знаков)
2. вычисляется их произведение n, которое не может быть разложено на множители за разумное время. Данное произведение называется модулем
3. Вычисляется значение функции Эйлера
φ(n) = φ(pq) = (p − 1)(q − 1).
4. Выбирается целое число e (1<e<(n)), взаимно простое со значением (n). Обычно в качестве e берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537. Число e называется открытой экспонентой
5. Вычисляется число d, удовлетворяющее условию:
de1(mod(n))
или в другом виде:
de=1+k(n)
Число d называется секретной экспонентой
6. Пара P = (e,n) публикуется в качестве открытого ключа системы RSA.
7. Пара S = (d,n) называется секретным ключом RSA и держится в тайне.
1. Шифрование сообщения
Чтобы зашифровать данные по известному ключу P = (e,n) необходимо разбить шифруемый текст на боки, каждый из которых может быть представлен в виде числа M(i) = 0, 1, … , n-1. Далее текст шифруется как последовательность чисел M(i), преобразованных по следующей формуле:
C(i) = M(i)emod(n)
2. Расшифровка сообщения
Чтобы расшифровать сообщение используя секретный ключ P=(d,n) необходимо каждое число из последовательности в зашифрованном сообщении преобразовать по формуле:
M(i) = C(i)dmod(n)
В результате будет получено множество чисел M(i), которое представляет собой исходный текст.