1.2. Теоретическая часть и расчет

1.2.1.Интервал дискретизации.

В АЦП преобразовывается непрерывное сообщение в дискретный (цифровой) сигнал, то есть в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Операция преобразования непрерывного сообщения в дискретное называется дискретизацией.

Дискретизация осуществляется не только по времени (как в импульсных методах модуляции), но и по уровням. Дискретизация по времени выполняется путем взятия отсчетов функции в определенные дискретные моменты времени . В результате непрерывная функциязаменяется совокупностью мгновенных значений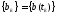. Моменты отсчетов на оси времени выбираются равномерно, т.е..

При дискретизации получают выборочные значения из непрерывного аналогового сигнала. Эти значения являются скалярным произведением функции , определяющей этот сигнал, и обобщенной функции, равной сумме бесконечного числа дельта-функций:

(1.1)

Интервал 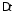называется интервалом дискретизации. Его величина выбирается в соответствии с теоремой Котельникова, согласно которой дискретизация не приводит к искажениям, если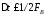, где– верхняя граничная частота спектра.

Устройство, с помощью которого ведется дискретизация, называется дискретизатором. Он является частью АЦП. В этом качестве можно использовать управляемый ключ, замыкаемый на непродолжительное время.

Таким образом, подставив в формулу вместо-, получим интервал дискретизации:

∆t=0.3846∙10^-3(c)=0.39(мс) (1.2)

1.2.2. Интервал квантования.

Полученные в результате дискретизации выборочные значения переводят в двоичные числа либо с их округлением, либо с усечением. Вначале каждое значение сравнивается с заранее заданными постоянными уровнями, которые называются уровнями квантования. Затем ближайший к выборочному значению уровеньпереводится в двоичное число.

Процесс замены выборочного значения ближайшим к нему уровнем называется квантованием.

Однако при квантовании возникает ошибка (погрешность), обусловленная округлением или усечением выборочных значений:

(1.3)

Рисунок 1.1 - Диаграмма, поясняющая процесс квантования

Амплитудная характеристика квантователя представлена в виде сплошной ступенчатой линии. Высота ступеньки определяется значением младшего разряда в двоичном представлении. Это шаг квантования, равный . Пунктирной линией показана характеристика идеального квантователя, когда число разрядов двоичного числа выбрано равным_∞. Ошибка, возникающая при округлении, удовлетворяет неравенству . Если значениенаходится между точками б, в, то погрешность округления будет отрицательной, но не более, а если между точками а, б – положительной.

Величина погрешности тем меньше, чем больше уровней квантования L, т.е. чем больше число разрядов двоичного числа. Однако увеличение числа разрядов приводит к усложнению устройств ЦОС и снижению их быстродействия.

Так как по условию в АЦП используется линейная шкала квантования с числом уровней L=256, случайный сигнал распределен по нормальному закону, т.е. все его значения распределены в диапазоне относительно среднего значения, то шаг квантования:

(1.4)

Таким образом, ∆b=0,014.

1.2.3. Мощность шума квантования.

Одной из причин, приводящих к отличию принятого сообщения от переданного в системе с ИКМ, является шум квантования. Погрешность (ошибку) квантования, представляющую собой разность между исходным сообщением и сообщением, восстановленным по квантованным отсчетам, называют шумом квантования. Шум квантования не связан с помехами в канале и целиком определяется выбором числа уровней квантования.

Т.е шум квантования – это совокупность разностей между отсеченными значениями первичного сигнала (сообщения) и ближайшими к этим значениям уровнями квантования. При равномерном квантовании, которое наиболее распространено на практике, максимальное значение шума квантования не превосходит половины интервала квантования, т.е.

(1.5)

Если полный размах непрерывного первичного сигнала равен, то число уровней квантования

(1.6)

При L=1 принято считать, что шум квантования распределен по равномерному закону в интервале от до.

Средняя мощность шума квантования

(1.7)

Шум квантования можно сделать сколь угодно малым, увеличивая число уровней. При этом придется увеличивать число кодовых символов, приходящихся на каждый отсчет, а следовательно, сокращать длительность символа и расширять спектр сигнала в канале.

Таким образом, подставив в формулу (1.6) шаг квантования ∆b=0,014, найдем значение мощности шума квантования:

P_ε=1.615∙10^-5(B²).

1.2.4. Отношение мощности первичного сигнала к мощности шума квантования в дБ.

Ненормированное сообщение имеет среднюю мощность

, (1.8)

где ,–пик-фактор сообщения,. Тогда отношение сигнал-шум квантования:

(1.9)

Это отношение зависит от числа уровней L квантования и связанного с этим уровнем длины n двоичной кодовой комбинации. Выбирая число уровней квантования (число разрядов n двоичного кода) можно снизить влияние шума квантования на верность передачи до минимума. Добавление каждого двоичного символа в кодовой комбинации (увеличение разрядности кода) улучшает отношение сигнал-шум приблизительно на 6 дБ. Однако, как уже отмечалось ранее, это приводит к требованию повышения быстродействия многоразрядных кодирующих устройств, расширения полосы частот канала передачи, увеличению сложности ЦАП и АЦП и ширины спектра двоичной кодовой комбинации.

Отношение мощности первичного сигнала к мощности шума квантования в дБ вычисляется по формуле:

(1.10)

Таким образом, A= 43,36 (дБ).

1.2.5. Производительность дискретного источника на выходе квантователя.

Некоторые источники передают сообщения с фиксированной скоростью, затрачивая в среднем время T на каждое сообщение.

Энтропия дискретного источника, отнесенная к среднему времени передачи одного символа T, называется производительностью источника дискретных сообщений:

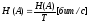. (1.11)

В нашем случае, производительность дискретного источника на выходе квантователя определяется энтропией квантованного сигнала источника, отнесенной к среднему времени передачи одного символа:

, (1.12)

где – время передачи одной квантованной выборки.

Для того чтобы определить энтропию, сначала необходимо определить априорные вероятности появления символов на выходе источника сообщений по формуле:

, (1.13)

где 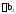- бесконечно малый интервал, равный по величине интервалу квантования, в середине которого находится значение символа;- значение плотности распределения в точке.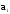

Зная априорные вероятности появления символов на выходе источника дискретных сообщений, можно определить энтропию дискретного источника, воспользовавшись формулой:

. (1.14)

Т.е. H_KB(А)= 2.408 (бит)

Таким образом, подставив значение энтропии дискретного источника в формулу (1.12), получим производительность источника дискретных сообщений на выходе квантователя:

Н’(A)=6.261∙10³ (бит/с).

1.2.6. Скорость цифрового потока на выходе квантователя.

Скорость передачи информации равна количеству взаимной информации, деленному на среднее время передачи одного символа:

(1.15)

Вычислим скорость передачи информации по двоичному симметричному каналу (см.рис.1.4.)

Рисунок 1.2 - Переходные вероятности в двоичном симметричном канале

На вход канала поступают символы ис вероятностямии, причем. На выходе канала присутствуют двоичные символыи. Вероятность ошибки при передаче любого символа равнаP. Переходные вероятности: .

Вычислим взаимную информацию по формуле:

. (1.16)

Энтропия

, (1.17)

где .

Условная энтропия при

. (1.18)

Подставляя ив формулу (1.16), получим

. (1.19)

При отсутствии помех ,, скорость равна. При,, скорость передачи равна нулю.

Будем считать, что в нашем канале помехи отсутствуют, т.е. . Это означает, что скорость цифрового потока на выходе квантователя равна производительности источника дискретных сообщений:

. (1.20)

Таким образом,

R = 6.261∙10³(бит/с).

1.2.7. Вероятности появления символов двоичных кодовых слов на выходе АЦП.

При кодировании каждое выборочное значение преобразуется в одно из L возможных значений, которое далее преобразуется в двоичное кодовой слово, длина которого . Энтропия, приходящаяся на один элемент двоичной кодовой последовательности, уменьшается в 8 раз (т.к.):

(1.21)

Т.е.

Н_Д (А)=0.301 (бит).

Для того чтобы найти вероятность появления символов двоичных кодовых слов на выходе АЦП, необходимо решить систему уравнений с двумя неизвестными:

, (1.22)

где p(0) – вероятность появления символа «0»; p(1) – вероятность появления символа «1».

Таким образом, решив систему (2.21), вероятности появления символов двоичных кодовых слов на выходе АЦП:

р(0)=0,665,

Р(1)=0,335.

1.2.8 Скорость цифрового потока на выходе АЦП.

Скорость цифрового потока на выходе АЦП равна скорости цифрового потока на выходе квантователя и определяется формулой:

. (1.23)

Таким образом, R_АЦП (А)=6.261∙10³(бит/с).

1.2.9. Дифференциальная энтропия источника непрерывных сообщений.

Энтропия - математическое ожидание количества информации.

Пусть – непрерывная случайная величина с плотностью распределения вероятности. Эта величина является отсчетом непрерывной случайной функции в некоторый момент времениt. Разобьем диапазон изменения непрерывной случайной величины на конечное число N малых интервалов шириной . Посколькумало, вероятность того, что случайная величинанаходится в пределахi-ого отрезка

(1.24)

Аналогично можно найти вероятность того, что случайная величина будет находиться в пределах любого другого отрезка.

Тогда, располагая рядом дискретных значений вероятностей, можно вычислить энтропию.

(1.25)

где N – число полученных дискретных значений. Увеличивая число N за счет уменьшения , в пределе получим выражение для энтропии непрерывной случайной величины:

(1.26)

Первое слагаемое полученного выражения имеет конечное число значений.

Обозначим его :

(1.27)

Второе слагаемое зависит от шага квантования и при стремится к. Это значит, что среднее количество информации, содержащееся в одном отсчете непрерывной случайной функции (сообщении) также равно бесконечности.

По этой причине величина не может быть количественной мерой, которая позволила бы оценить объем информации, содержащейся в одном отсчете непрерывной случайной функции (сообщении).

В качестве этой меры принимают первое слагаемое выражения (1.25) и отбрасывают второе. Т.к. первое выражение зависит от дифференциальной плотности распределения вероятности, оно получило название дифференциальной энтропии и обозначается . Дифференциальная энтропия позволяет оценить среднее количество информации, которое содержится в непрерывных сообщениях или непрерывных сигналах.

Для двух непрерывных случайных величин и, которые характеризуются двумерной плотностью распределения вероятности, можно определить условную дифференциальную энтропию.

Условная дифференциальная энтропия непрерывной случайной величины при известной случайной величине:

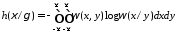(1.28)

Условная дифференциальная энтропия непрерывной случайной величины при известной случайной величине:

(1.29)

Дифференциальную энтропию, в отличие от энтропии дискретной случайной величины, нельзя рассматривать как меру собственной информации. Она является относительной мерой неопределенности и не обладает рядом ее свойств. В частности, она может быть как положительной, так и отрицательной. Информационный смысл имеет не сама дифференциальная энтропия, а разность двух дифференциальных энтропий, чем объясняется ее название. Впрочем, свойство аддитивности сохраняется и для дифференциальной энтропии. Значение дифференциальной энтропии зависит от масштаба случайной величины, а следовательно, от выбора единицы ее измерения.Также, дифференциальная энтропия гауссовской случайной величины не зависит от ее математического ожидания и монотонно возрастает с увеличением дисперсии.

1) Плотность распределения случайного первичного сигнала, поступающего на вход АЦП, починена нормальному закону распределения:

, (1.30)

где _α – среднее значение первичного сигнала, равное по условию нулю;

–дисперсия (мощность).

Для определения дифференциальной энтропии воспользуемся формулой (1.26):

(1.31)

Первый интеграл равен 1, второй – . Поэтому:

_(1.32)

Учитывая, что соизмеримо с, и подставив, получим дифференциальную энтропию источника непрерывных сообщений:

h(ξ)=0.388 (B).

Найдем избыточность источника дискретных сообщений:

(1.33)

Тогда μ=1.01∙10³ (В/с).