Используя формулы (10) и (11), находим

(3.12)

После соприкосновения груза со столом сила упругости Т обращается в нуль (нить должна в момент соприкосновения соскользнуть со шкива). Дальнейшее вращение маятника под действием сил трения в опоре становится замедленным и описывается уравнением

(3.13)

Предполагая, что в течение всего времени вращения маятника момент сил трения в опоре не изменяется, т.е. , уравнение (3.13)можно проинтегрировать следующим образом:

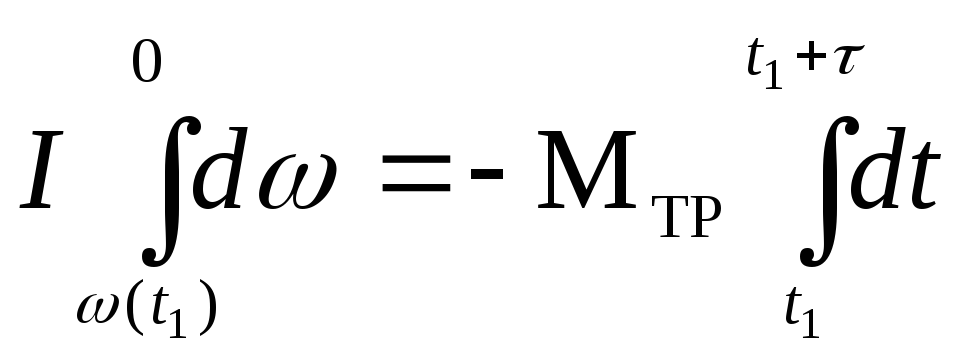, (3.14)

где - угловая скорость в момент соприкосновения груза со столом, - промежуток времени от момента соприкосновения груза со столом до остановки маятника. Это время измеряется секундомером ЭС-2. Элементарное интегрирование приводит уравнение (3.14) к виду

. (3.15) Учитывая теперь, что , из (3.10) с помощью (3.11) находим

(3.16)

Подстановка в (3.15) дает

(3.17)

Принимая во внимание соотношения (3.11), (3.12), (3.17) и вводя диаметр шкива , систему уравнений (3.8), (3.9) можно представить в виде

(3.18)

(3.19)

Уравнения (3.18) и (3.19) образуют систему двух уравнений с двумя неизвестными I и Т. Все остальные входящие в них величины, за исключением g=9,8 м/с², определяются экспериментально в прямых измерениях.

Исключая из (3.19) с помощью (3.18) неизвестную Т, получаем формулу для измерения момента инерции крестообразного маятника относительно оси вращения

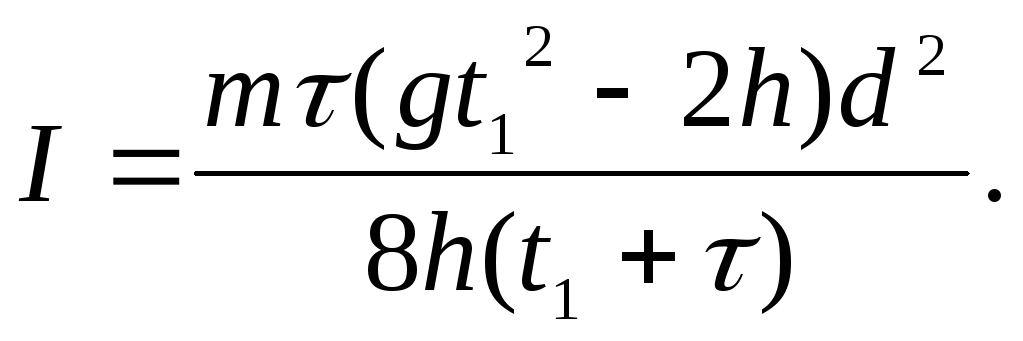(3.20)

Изменяя массу подвешенного к нити груза, можно изменять силы упругости нити и трения в опоре (а, следовательно, и их моменты). Однако при этом, как следует из уравнения движения (3.9), при заданном расположении грузов m на стержнях маятника или при их отсутствии отношение модулей суммарного момента сил и углового ускорения маятника должно оставаться неизменным, т.е.

Это следует из определения момента инерции как физической величины. Следовательно, если, проделав опыт с различными грузами m₁,m₂,m₃…, мы получим в результате расчетов по формуле (3.20) одинаковые значения моментов инерции маятника I₁,I₂,I₃…, то можно сделать заключение о справедливости уравнения вращательного движения маятника (3.9). При этом результаты косвенных измерений считаются одинаковыми в пределах погрешностей, т.е. I₁=I₂=I₃=…, если пересекаются их доверительные интервалы. Практически это легко установить, отложив на вещественной оси в выбранном масштабе средние значения , окруженные соответствующими доверительными интервалами ,,…,

При проверке свойства аддитивности момента инерции (т.е. того, что момент инерции тела относительно некоторой оси равен сумме моментов инерций любых частей этого тела относительно той же оси) и изучении характера зависимости момента инерции крестообразного маятника от распределения масс относительно оси вращения, будем обозначать момент инерции маятника без грузов m на стержнях (рис.3.2) через , а с закрепленными на них четырьмя грузами – через . Тогда, пренебрегая размерами грузов по сравнению с размерами стержней, в соответствии со свойством аддитивности момента инерции можно записать

, (3.21)

где l – расстояние от центра закрепленного на стержне груза до оси вращения, m - масса одного груза. Как видно из рис. 3.2,

, (3.22)

где d –диаметр шкива, х – длина закрепленного груза, S – расстояние до ближайшего торца этого груза.