
- •Алгоритмы компьютерной графики
- •Введение
- •Отображение просранства пользователя и машинного носителя
- •Расчет пользовательских и машинных координат
- •Алгоритмы генерирования линий.
- •Генерирование отрезка прямой. Алгоритм Брезенхема
- •Формирование дуги окружности.
- •Кривые Безье.
- •Двумерное отсечение
- •Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.
- •Отсечение выпуклым многоугольным окном. Алгоритм Кируса-Бэка
- •Определение выпуклости многоугольника.
- •Отсечение невыпуклым многоугольником.
- •Заливка областей.
- •Заливка с сортировкой
- •Заливка по ребрам.
- •Cписок активных ребер.
- •Заливка с затравкой.
- •Преобразование координат
- •Преобразования координат в двумерной системе.
- •Преобразования в трех мерной системе координат
- •Двумерные проекции
- •Виды проекций
- •Перспективные проекции
- •Определение координат точки на плоскости проекции
- •Xэ, Yэ - оси системы координат на плоскости проекции (на экране).
- •Точки и линии схода
- •Косоугольные проекции
- •Аксонометрическая проекция
- •Построение проекций трехмерных объектов
- •Затенение отрезка плоскостью при перспективной проекции
- •Удаление затеняемых ребер в аксонометрической проекции
- •Алгоритмы параллельной обработки графической информации
- •Построение сечения объекта.
Определение выпуклости многоугольника.
Алгоритм Кируса–Бэка предполагает наличие выпуклого многоугольника, используемого в качестве окна.
Однако на практике весьма часто возникает задача отсечения многоугольником, а информация о том, является он выпуклым или нет изначально не задается. В таком случае, прежде чем начать процедуру отсечения необходимо определить какой задан многоугольник – выпуклый или нет.
Дадим некотрые определения выпуклости многоугольника
Выпуклым считается многоугольник, для которого выполняется одно из ниже перечисленных условий:
в выпуклом многоугольнике все вершины располагаются по одну сторону от линии, несущей любое ребро (по внутреннюю сторону относительно данного ребра);
все внутренние углы многоугольника меньше 180о;
все диагонали, связывающие вершины многоугольника, лежат внутри этого многоугольника;
все углы многоугольника обходятся в одном направлении ().
Для выработки аналитического представление последнего критерия выпуклости, используем векторное произведение.
Векторное произведение W двух векторов a и b (Рис. 3.3 -31 а) определяется как:
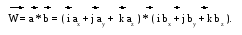
где:
ax,ay,az и bx,by,bz являются проекциями на оси координат X,Y,Z, соответственно, векторов – сомножителей a и b,
i, j, k – единичные векторы по координатным осям X, Y, Z.

Рис. 3.3‑30


Рис. 3.3‑31
Если рассматривать двумерное представление многоугольника как представление его в координатной плоскости XY трехмерной системе координат X,Y,Z (Рис. 3.3 -31 b), то выражение для формирования векторного произведения векторов U и V , где векторы U и V являются соседними ребрами, образующими угол многоугольника, можно записать в виде определитель:

Вектор векторного произведения перпендикулярен плоскости, в которой находятся вектора-сомножители. Направление вектора произведения определяется по правилу буравчика или по правилу винта с правой нарезкой.
Для случая, представленного на Рис. 3.3 -31 b), вектор W, соответствующий векторному произведению векторов V,U, будет иметь ту же направленность, что и направленность координатной оси Z.
Учитывая то, что проекции на ось Z векторов –сомножителей в этом случае равны нулю, векторное произведение можно представить в виде:
 (3.3-1)
(3.3-1)
Единичный вектор k всегда положительный, следовательно, знак вектора векторного произведения будет определяться только знаком определителя в выше приведенном выражении. Отметим, что на основании свойства векторного произведения, при перестановке местами векторов-сомножителей U и V знак вектора будет меняться на противоположный.
Отсюда следует, что, если в качестве векторов V и U рассматривать два соседних ребра многоугольника, то порядок перечисления векторов в векторном произведении можно поставить в соответствие c обходом рассматриваемого угла многоугольника или ребер, образующих этот угол. Это позволяет использовать в качестве критерия определения выпуклости многоугольника правило:
если для всех пар ребер многоугольника выполняется условие:

Если знаки векторных произведений для отдельных углов не совпадают, то многоугольник не выпуклый.
Так как ребра многоугольник задаются в виде координат их концевых точек, то для определения знака векторного произведения удобнее использовать определитель:

Легко показать, что этот определитель эквивалентен определителю в выражении (3.3-1).
