1.2. Линейное нормированное пространство

Часто в приложениях необходимо использовать понятие «близость» элементов. Если, например, мы хотим сравнить два сигнала f(x) и g(x), то как нам оценить, близки эти сигналы или не очень?

Рис. 1.1 Близость функций

В повседневной жизни близость мы привыкли оценивать расстоянием между объектами. Если рассматриваемые объекты есть числа f=const, и g=const, то расстояние между точками f и g на числовой оси есть просто модуль разности . Чем ближеf к g, тем меньше . А как оценить близость между двумя функциями f(x) и g(x) (векторами , матрицамиA, B)? Что такое «близко» для этих объектов?

Оказывается, в зависимости от выбранного класса функций (непрерывные, разрывные, но интегрируемые, дифференцируемые) близость может трактоваться по-разному. Например, две функции f(x) и g(x) или f(x) и h(x) на рис. 1.1 в одних инженерных задачах могут считаться близкими, а в других – нет. Ввиду этого должны быть предложены математические модели расстояний, различные для функций (матриц, векторов) из разных классов. Обычно при выполнении расчетов имеют дело с объектами, являющимися элементами некоторого нормированного пространства.

Нормированным называется такое линейное пространство, каждому элементу которого поставлено в соответствие число ║x║ (норма x), удовлетворяющее следующим аксиомам:

1. норма (положительное число).

2. , только приx =  ( – нулевой элемент).

3. ,a число (может быть комплексным).

4. неравенство треугольника.

Расстояние между элементами в нормированном пространстве определяется через норму:

.

В зависимости от класса рассматриваемых объектов норма, а следовательно, и расстояние, вводятся по-разному. Наиболее часто используются следующие нормированные пространства.

Рис. 1.2 Расстояние в С

Пространство непрерывных функций C[a,b] – множество непрерывных действительных функций {f(x), g(x), h(x), …}, определенных на интервале [a, b].

Норма и расстояние в C[a, b] определяются по формулам:

.

На рис. 1.2 представлена геометрическая иллюстрация расстояния в пространстве С[a, b].

Рис. 1.3 Расстояние в L2

Пространство интегрируемых с квадратом функций L₂[a, b] – множество функций, для которых .

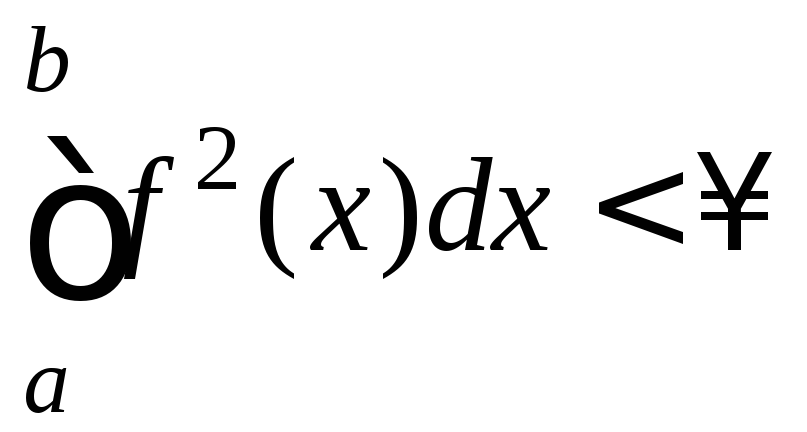В L₂[a, b] имеются и разрывные функции, т. е. C[a, b]  L₂[a, b].

Норма и расстояние в L₂[a, b] (рис.1.3):

Заметим, что функции f и g на рис. 1.1 будут «близкими» в пространстве L₂ и «далекими» в пространстве С, т. е. норма в С более «сильная»:

.

Пространство Соболева – множество функций, имеющих интегрируемые с квадратом производные до s порядка. Норма определяется как , расстояние .В этом пространстве близость между функциями характеризует также близость их производных. Например, функции f и h на рис. 1.1 будут «близкими» по норме и «далекими» по норме , причем .

Во множестве векторов нормы также можно ввести по-разному:.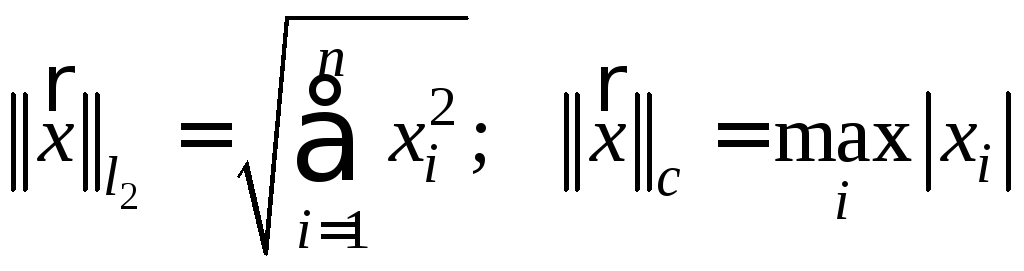

Во множестве квадратных матриц наиболее употребительны следующие нормы (_i -собственные значения матрицы А):

.

Фундаментальной последовательностью элементов метрического пространства Х называется такая бесконечная последовательность {}, для которойпри.

Любая фундаментальная последовательность x_n сходится при n   к некоторому пределу.

Метрическое пространство Х называется полным, если в нем любая фундаментальная последовательность элементов x_i  Х сходится к пределу, являющемуся элементом пространства Х.

Например, пространство Х=(0,) c расстоянием является неполным, т. к. последовательность, но ноль не принадлежитХ. Если замкнуть это пространство, включив в него нулевой элемент, получим полное пространство Х=[0,). Аналогично, множество рациональных чисел отрезка прямой является неполным, т.к. всегда найдется последовательность из рациональных чисел, сходящаяся к иррациональному числу.