
flash Лебедев / Новый вариант / ! / ТАУ_руков.по лаб
..pdf
11
Wрц( p) =Wpg ( p) Woc ( p) = |
|
|
k1k2k3koc (T2 p +1) |
|
|
|
; |
|
|||||||||||||||||||||||||||
(T 2 p2 +2ξT p +1)(T p +1) |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
- передаточная функция замкнутой системы по за- |
|||||||||||||||||||||||||||||||||||
дающему воздействию: |
|
|
|
|
|
k1k2k3(τ2 p +1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Wpg ( p) |
|
|
|
(T 2 p2 |
+ 2ξT p |
+1)(T p |
+ |
1) |
|
|
|
|
|
|||||||||||||||||||
Wзg ( p) = |
|
|
|
|
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
= |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
k1k2k3koc |
(τ2 p +1) |
|
|
|
|
|
|
||||||||||||||||
1+W |
( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
pц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ (T |
2 p2 + 2ξT p |
+1)(T p |
+1) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
= |
|
|
|
|
|
|
|
|
k1k2k3(τ2 p +1) |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||
(T 2 p2 |
+2ξT p +1)(T p +1)+k k |
|
k k |
oc |
(τ |
2 |
p +1) |
|
|
|
|
||||||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
1 |
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
- передаточная функция замкнутой системы по воз- |
|||||||||||||||||||||||||||||||||||
мущающему воздействию: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Wpf ( p) |
|
|
|
|
|
|
|
|
|
|
|
k3k4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T p + |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Wзf ( p) = |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
k1k2k3koc (τ2 p +1) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
1+W |
|
( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
pц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ (T |
2 p2 |
+ |
2ξT p +1)(T p +1) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= (T 2 p2 + |
|
|
k k (T 2 p2 +2ξT p +1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2ξT p +1)(T p + |
1)+k k k k (τ p +1); |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
1 2 |
3 |
oc |
|
|
|
2 |
|
|
|
|
|||||
Знаменатель передаточных функций замкнутой системы называется ее характеристическим полиномом, который в нашем случае будет иметь вид:
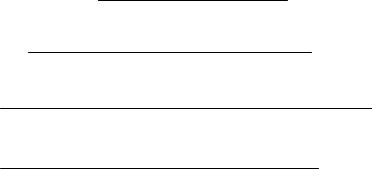
A( p) = (T12 p2 +2ξT1 p +1)(T3 p +1)+k1k2k3koc (τ2 p +1)=
= a3 p3 +a2 p2 +a1 p +a0,
причем коэффициенты этого полинома будут равны:
a0 = Kp +1; a1 = 2ξT1 +T3 + Kpτ2; a2 =T1(T1 + 2ξT3 ); a3 =T12T3,
где Kp = k1k2k3koc = 50 – коэффициент передачи разомкнутой цепи системы.
12
4.3.Определение устойчивости САУ по критерию Найквиста и расчет граничного коэффициента передачи разомкнутой цепи
В соответствии с критерием Найквиста, САУ будет устойчивой, если годограф АФЧХ ее разомкнутой цепи не охватывает точку с координатами (−1; j0) на комплексной плоскости при
изменении частоты ω от нуля до бесконечности. Иначе говоря, |
||
для устойчивой САУ необходимо выполнение условий: |
||
Re[W |
( jω)]< −1, |
|
|
рц |
( jω)]=0, |
Im[W |
||
|
|
(4.1) |
рц |
|
|
где Re[Wрц( jω)]и Im[Wрц( jω)] – вещественная и мнимая части
АФЧХ разомкнутой цепи системы Wрц( jω), полученной из передаточной функции Wрц(p) путем замены оператора p на опе-
ратор jω.
В рассматриваемой задаче АФЧХ разомкнутой цепи сис-
темы будет иметь вид: |
|
Kp ( jωτ2 +1) |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Wрљ( jω)= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
(1−T 2ω2 +2 jωξT )( jωT +1) |
= |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
( jωτ2 |
+1) |
1 |
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Kp |
|
|
|
|
|
|
|
|
|
|
||||
|
|
= |
[1−T |
(T +2ξT )ω2 |
]+ jω[2ξT |
|
+T |
(1−T |
2ω2 )]= |
2ω2 )]} |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
3 |
|
|
|
1 |
3 |
|
1 |
|
|
|
|
||||||
= |
K |
p |
( jωτ |
2 |
+1){[1−T |
(T |
+2ξT |
)ω2 ]− jω[2ξT |
+T (1 |
−T |
= |
|||||||||||||||
|
|
|
|
|
|
|
1 |
1 |
|
3 |
|
|
|
|
1 |
3 |
|
1 |
||||||||
|
|
|
|
[1−T |
(T |
+2ξT )ω2 ]2 +ω2 [2ξT +T (1−T 2ω2 )]2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
3 |
|
|
|
[2ξT |
1 |
|
3 |
1 |
|
|
|
|
||
|
K |
p |
{1−T (T |
+2ξT )ω2 |
+ω2τ |
2 |
+T |
|
(1−T 2ω2 )]} |
|
|
|
||||||||||||||
|
|
|
|
1 |
|
1 |
|
3 |
|
|
|
|
1 |
3 |
|
1 |
|
|
|
|
|
|||||
= |
[1−T |
(T |
|
+2ξT )ω2 ]2 |
+ω2[2ξT +T (1 |
−T 2ω2 )]2 |
|
+ |
|
|
||||||||||||||||
|
|
|
1 |
|
1 |
|
|
3 |
|
|
|
|
1 |
|
3 |
|
1 |
|
|
|
|
|
|
|||

13
+ jω K[p {τ2 [1−T1(T1 + 2ξT]3 )ω2 ]−[[2ξT1 +T(3(1−T12ω)2])]}.
1−T1(T1 + 2ξT3 )ω2 2 +ω2 2ξT1 +T3 1−T12ω2 2
Таким образом, действительная и мнимая части АФЧХ описываются выражениями:
Re[W |
|
( jω)]= |
|
K |
p |
{1−T (T +2ξT )ω2 |
+ω2τ |
2 |
[2ξT +T |
(1 |
−T 2ω2 )]} |
|||||||||||||||||||
|
|
|
|
|
|
|
1 1 |
|
3 |
|
|
|
|
1 |
|
3 |
1 |
|
|
|
, |
|||||||||
|
|
|
|
[1−T |
(T +2ξT )ω2 ]2 |
+ω2[2ξT +T |
(1−T 2ω2 )]2 |
|
|
|||||||||||||||||||||
|
рљ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ω{τ |
1 |
1 |
3 |
|
|
|
1 |
|
3 |
|
1 |
|
|
|
|
|
||||
Im[W |
( jω)]= |
K |
|
2 |
[1−T |
(T + |
2ξT )ω2 ]−[2ξT +T |
(1−T 2ω2 )]} |
|
|||||||||||||||||||||
|
|
|
p |
|
|
1 1 |
3 |
|
|
|
|
1 |
|
3 |
|
1 |
|
. |
|
|||||||||||
|
|
[1−T (T +2ξT )ω2 ]2 |
+ω2[2ξT +T |
|
(1 |
−T 2ω2 )]2 |
|
|||||||||||||||||||||||
|
рц |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
3 |
|
|
|
1 |
|
3 |
|
|
1 |
|
|
|
|
|
|||
|
Приравняв выражение для мнимой части АФЧХ нулю, |
|
|
|
|
|||||||||||||||||||||||||
рассчитаем квадрат частоты переворота фазы ωπ2 : |
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
|
2ξT1 |
+T3 −τ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ωπ |
= |
T 2T −τ |
2 |
(T 2 + 2ξT T )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
3 |
|
|
|
|
|
1 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0,8 0,3 +0,5 −0,1 |
|
|
|
|
|
|
|
|
рад |
2 |
|
|
|
|||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 73,333 |
|
|
. |
|
||||||
|
|
|
0,32 |
0,5 −0,1(0,32 + 2 0,5 |
0,3 0,8) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|||||||||||||||||
Подставив значение ωπ2 в выражение для действительной части АФЧХ, получим следующее число при Kp =50 :
Re[Wрц( jω)] =
= K[p {1−T1(T1 + 2ξT3 )ωπ]2 +ωπ2τ[2 [2ξT1 +T(3(1 −T12ωπ)]2 )]}= −2,155.
1−T1(T1 + 2ξT3 )ωπ2 2 +ωπ2 2ξT1 +T3 1 −T12ωπ2 2
Так как полученное число по модулю больше, чем -1, то САУ неустойчива.
Определим граничный коэффициент передачи для заданной САУ. Для этого приравняем действительную часть АФЧХ
значению 1 Тогда граничный коэффициент передачи будет
ω=lg =1 2 τ2 .
рассчитываться по формуле:

14
Kp,гр = −[1−T1(T1 + 2ξT3)ωπ2 ]2 +ωπ2[2ξT1 +T3(1−T12ωπ2 )]2 .
1−T1(T1 + 2ξT3)ωπ2 +ωπ2τ2[2ξT1 +T3(1−T12ωπ2 )]
После подстановки в эту формулу заданных значений по-
стоянных времени и квадрата частоты переворота фазы ωπ2 получим следующую величину граничного коэффициента переда-
чи Kp,гр = 23,2 .
П р и м е ч а н и е . Если в структуре САУ не содержится форсирующих звеньев, то при выделении вещественной и мнимой частей АФЧХ операция умножения числителя АФЧХ на комплексное число, сопряженное знаменателю, не является обязательной. Действительно, пусть выражение АФЧХ имеет вид
W ( jω) = |
Kp |
, где a, b, c и d – константы, отлич- |
|
(a + b) + j(c + d) |
|||
|
|
ные от нуля. Домножим числитель и знаменатель на выражение,
сопряженное выражению, |
расположенному в знаменателе. То- |
|||||||
гда получим W ( jω) = |
|
Kp |
[(a + b) - j(c + d)] |
. Так как по крите- |
||||
|
(a + b)2 + (c + d)2 |
|
||||||
|
|
|
|
|
||||
рию устойчивости Найквиста Im[W ( jω)]= −(c +d ) = 0 , |
то ее |
|||||||
можно исключить |
из |
выражения АФЧХ, то |
есть |
|||||
Re[W ( jω)]= |
Kp (a +b) |
= |
Kp |
. |
|
|
||
(a +b)2 |
|
|
|
|||||
|
|
a +b |
|
|
||||
4.4. Анализ устойчивости САУ по критерию Гурвица и построение ее области устойчивости в плоскости варьируемых параметров x1 и x2
Исходным материалом для исследования устойчивости САУ по критерию Гурвица является ее характеристический полином A(p). Система третьего порядка будет устойчивой, если выполняется неравенство
15
2 |
= |
a2 |
a0 |
= a a |
2 |
−a a > 0 , |
(4.2) |
|
|
a3 |
a1 |
1 |
3 |
0 |
|
||
|
|
|
|
|
|
|
||
где a0 , a1, a2 , a3 – коэффициенты характеристического поли-
нома.
На границе устойчивости должно выполняться равенство:
|
|
a1a2−a3a0 = 0 , |
|
|
|
(4.3) |
||
|
|
В рассматриваемом случае |
|
|
||||
a0 |
= Kp +1 =51; |
|
a1 = 2ξT1+T3 + Kpτ2 =5,98 c; |
|||||
|
|
=T (T + 2ξT )= 0,33 c2 |
|
|
|
. |
||
a |
2 |
; |
a |
=T 2T = 0,045 c3. |
||||
|
1 |
1 |
3 |
|
3 |
1 |
3 |
|
Оценим устойчивость САУ по условию (4.2):
a1a2 −a0a3 =5.98 0,33 −51 0,045 = −0,322 .
Т.к. условие (4.2) (положительность главного минора определителя Гурвица 2 ) не выполняется, то система неустойчи-
ва.
Пусть варьируемыми параметрами являются коэффициент передачи и постоянная времени первого звена САУ, то есть
x1 =T1 |
и x2 = k1 . |
Введем третий варьируемый параметр |
|||
x3 = Kp |
и выведем расчетные соотношения для параметров x1 |
||||
и x , так как x |
= |
|
x3 |
. В этом случае выражения для коэф- |
|
|
|
||||
3 |
2 |
|
k2k3koc |
||
|
|
|
|||
фициентов характеристического полинома примут вид:
a0 (x3) = x3 +1; |
|
a1(x1, x3) = 2ξx1 +T3 + x3τ2; |
|||||||
a |
2 |
(x ) = x (x + 2ξT ); |
a (x ) = x 2T . |
||||||
|
1 |
1 |
1 |
3 |
3 |
1 |
1 |
3 |
|
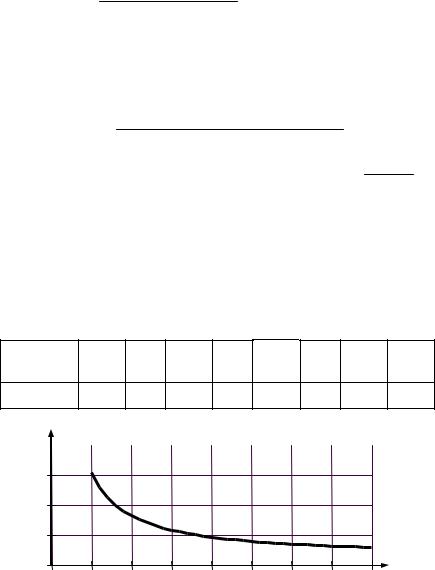
Подставим выражения коэффициентов в условие границы устойчивости (4.3) и разрешим полученное выражение относи-
тельно параметра x3 . Тогда получим:
(2ξx1 +T3 + x3τ2 )x1(x1 +2ξT3 )− x12T3(x3 +1)= 0 ;
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
x (x ) = |
2ξ(x 2 |
+T |
2 + 2ξx T ) |
|
|
|
|
|
(4.4) |
|||||||
|
|
|
|
1 |
3 |
|
1 3 . |
|
|
|
|
|
||||||
|
|
3 |
1 |
|
|
x1T3 −τ2 (x1 + 2ξT3) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
При подстановке в качестве параметра x1 значения посто- |
|||||||||||||||||
янной времени T1 |
в выражение (4.4) рассчитывается граничное |
|||||||||||||||||
значение коэффициента передачи разомкнутой цепи, что явля- |
||||||||||||||||||
ется проверкой правильности выполнения п. 3.2.3 задания: |
|
|||||||||||||||||
K |
p,гр |
= x (T ) = 2 0,8 (0,32 +0,52 + 2 0,8 0,3 0,5) = 23,2 . |
||||||||||||||||
|
|
3 |
1 |
|
|
0,3 0,5 −0,1 (0,3 + 2 0,8 0,5) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Путем простого пересчета |
|
по формуле |
x (x ) = |
x3(x1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
k2k3koc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
строится |
граница |
устойчивости |
|
САУ |
|
в области |
параметров |
|||||||||||
x1 =T1,гр |
и x2 = k1,гр . Результаты вычислений по формуле (4.4) |
|||||||||||||||||
приведены в табл. 4.1, а сама граница устойчивости изображена |
||||||||||||||||||
на рис. 4.1. |
|
Область устойчивости САУ будет располагаться |
||||||||||||||||
между кривой x2 = f (x1) и осями координат, поскольку именно |
||||||||||||||||||
здесь выполняется условие k1 < k1,‹р . |
|
|
|
|
|
|
||||||||||||
x1 = T1,гр , |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.1 |
|||||
0,225 |
0,25 |
0,275 |
|
0,3 |
0,325 |
0,35 |
0,375 |
0,4 |
||||||||||
|
с |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = k1,‹р |
|
15,38 |
8,2 |
5,82 |
4,64 |
|
3,94 |
3,48 |
3,157 |
2,192 |
||||||||
|
20 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
0.23 |
0.25 0.28 |
0.3 |
0.33 |
0.35 0.38 0.4 |
|
|||||||||||
|
|
|
Рис. 4.1. Граница устойчивости САУ |
|
|
|
||||||||||||
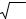
17
4.5.Построение логарифмических частотных характеристик САУ для заданного запаса устойчивости по амплитуде
Исходя из определения запаса устойчивости по амплитуде G, можно записать следующее уравнение:
G = 20 lg(Kр,гр) −20 lg(Kр) ,
где Kр и Kр,гр – коэффициент передачи разомкнутой цепи и
его граничное значение.
Решая это логарифмическое уравнение, можно рассчитать значение необходимого коэффициента передачи разомкнутой
цепи Kр , исходя из известного Kр,гр и заданного запаса устойчивости по амплитуде G:
Kр = |
|
Kр,гр |
|
|
|
|
. |
(4.5) |
|
|
G |
|||
|
10 20 |
|
|
|
В рассматриваемом задании, для |
G = 10 дБ, в соответст- |
|||
вии с формулой (4.5) принимается следующее значение Kр :
Kр = |
23,2 |
= |
23,2 |
= 7,336 , отсюда |
||
10 |
|
|||||
|
|
|
|
10 |
|
|
1020 |
|
|||||
|
|
|
|
|||
k |
= |
Kр |
= |
6,874 |
=1,467 . |
|
|
||||
1 |
|
k2k3kос |
|
2 5 0,5 |
|
|
|
|
|||
Логарифмические амплитудная G(ω) и фазовая ϕ(ω) ха-
рактеристики (ЛАЧХ и ЛФЧХ) строятся непосредственно по передаточной функции разомкнутой цепи системы, причем
m |
m |
|
||||
G(ω) =∑Gi (ω) =∑20 lg[ |
|
Wi ( jω) |
|
], |
(4.6) |
|
|
|
|||||
|
|
|
||||
i=1 |
i=1 |
|
||||

18
m |
m |
|
ϕ(ω) = ∑ϕi (ω) =∑arg[Wi ( jω)], |
(4.7) |
|
i=1 |
i=1 |
|
где Gi (ω) и ϕi (ω) – ЛАЧХ и ЛФЧХ i-го звена САУ с частотной характеристикой Wi ( jω); m – количество звеньев; arg – функция аргумента (для типовых звеньев может быть рассчитана через вещественную Pi (ω) и мнимую Qi (ω) частотные характеристики по формуле:
arg[Wi ( jω)]= arctg Qi (ω) .
При построении асимптотической ПАЧХ следует руководствоваться следующим алгоритмом:
- рассчитывается коэффициент передачи на частоте ω = 1 по выражениюG0 = 20 lg(Kp );
- рассчитываются частоты сопряжения ЛАЧХ звеньев
1
ωi = lg , где Ti – постоянная времени i-го звена;
Ti
- асимптотическая ЛАЧХ САУ строится по асимптотическим ЛАЧХ ее звеньев, причем следует помнить, что ЛАЧХ пропорционального звена имеет нулевой наклон во всем диапазоне частот, ЛАЧХ интегрирующего звена - наклон -20 дБ/дек во всем диапазоне частот, ЛАЧХ инерционного звена - нулевой наклон до частоты сопряжения и наклон -20 дБ/дек после этой частоты, ЛАЧХ форсирующего звена - нулевой наклон до частоты сопряжения и наклон +20 дБ/дек после этой частоты, ЛАЧХ колебательного звена - нулевой наклон до частоты сопряжения и наклон - 40 дБ/дек после этой частоты.
Ниже приведены расчетные соотношения для ЛФЧХ некоторых типовых звеньев:
ϕ(ω) = 0 – для пропорционального звена;
ϕ(ω) = − π – для интегрирующего звена;
2

19
ϕ(ω) = −arctg(ωT ) – для инерционного звена; ϕ(ω) = arctg(ωτ) – для форсирующего звена;
|
|
2ξωT |
|
|
|
|
|
1 |
|
|
|
|
|
−arctg |
|
|
|
|
|
при |
ω≤ |
|
|
, |
|
|
|
|
2 |
2 |
|
T |
|
|
|||||||
|
1 |
−ω T |
|
|
|
|
|
|
|
– |
для |
||
ϕ(ω) = |
|
2ξωT |
|
|
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
||||||
−arctg |
|
|
|
|
−π |
при |
ω> |
|
|
|
|
||
|
2 |
2 |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
T |
|
|||||
|
−ω T |
|
|
|
|
|
|
||||||
колебательного звена.
Проиллюстрируем действие описанного алгоритма для рассматриваемого задания. Рассчитаем значение коэффициента передачи на нулевой частоте
G0 = 20 lg(Kp )= 20 lg(7,336) ≈17,3 дБ.
|
Рассчитаем частоты сопряжения: |
||||||||
|
|
1 |
|
|
|
|
|||
ω1 |
|
|
|
|
|
|
|
дек – для колебательного звена; |
|
|
|
|
|
|
|||||
= lg T |
= 0,523 ≈ 0,5 |
||||||||
|
|
1 |
|
|
|
|
|||
|
|
1 |
|
|
|
|
|||
ω2 |
|
|
|
|
|
=1 дек – для форсирующего звена; |
|||
|
|
|
|||||||
= lg |
|
|
|
|
|||||
|
|
τ2 |
|
|
|||||
ω3 |
|
1 |
|
=0,301 ≈ 0,3 |
дек – для инерционного звена. |
||||
|
|||||||||
=lg T |
|
|
|||||||
|
|
3 |
|
|
|
|
|||
Для заданного варианта расчетная формула для ЛФЧХ будет иметь вид:
|
|
2ξωT |
|
|
+ arctg(ωτ |
|
)− arctg(ωT |
) при |
|
− arctg |
1 |
|
|
2 |
|||||
2 |
2 |
||||||||
|
|
|
|
3 |
|||||
|
1 − ω T1 |
|
|
|
|
|
|||
|
|
2ξωT |
|
|
|
|
|
|
|
|
|
− π + arctg(ωτ2 )− |
|
||||||
ϕ(ω) = − arctg |
1 |
|
|
|
|||||
1 − ω2T |
2 |
|
|||||||
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
− arctg(ωT ) |
|
|
|
|
|
при |
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ω ≤ 1 ,
T1
ω > 1 .
T1
На рис. 4.2а построена асимптотическая ЛАЧХ для заданной САУ. Она имеет нулевой наклон до частоты сопряжения
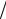
20
ω3 , соответствующей инерционному звену. Инерционное звено «включается» и ЛАЧХ приобретает наклон –20 дБ/дек. Этот наклон сохраняется до частоты сопряжения ω1 . Далее «срабаты-
вает» колебательное звено, и суммарный наклон ЛАЧХ становится равным –60 дБ/дек, который сохраняется до частоты со-
пряжения ω2 , соответствующей форсирующему звену. Оно снижает наклон ЛАЧХ до –40 дБ/дек и этот наклон остается неизменным при дальнейшем увеличении частоты. Частота ωcp ,
при которой ЛАЧХ пересекает ось lg(ω) (т.е. коэффициент передачи САУ становится равным единице), называется частотой среза и характеризует запас устойчивости САУ по фазе Δϕ.
На рис. 4.2б показана ЛФЧХ САУ, рассчитанная по приведенному выше выражению. Легко видеть, что начальный фазовый сдвиг составляет около –50°. Это обусловлено одновременным «действием» колебательного и инерционного звеньев. Затем фаза возрастает (по абсолютной величине) и на частоте
переворота фазы ωπ , определяющей запас устойчивости САУ
по амплитуде, становится равной –180°. После «включения» форсирующего звена фаза начинает уменьшаться (по абсолютной величине) и асимптотически стремится к значению –180°. Отрезок ϕ ≈16 °, образованный ЛФЧХ и линией, соответст-
вующей –180°, на частоте среза является запасом устойчивости САУ по фазе.
4.6. Расчет статических характеристик САУ
Регулировочная и внешняя статические характеристики САУ получается из передаточных функций путем замены в них оператора p на нуль. Таким образом, их уравнения будут иметь
вид:
y(g)| |
= g Wзg (0) = g |
k k |
2 |
k |
3 |
= g |
Kp koc |
|
1 |
|
|
– для регулиро- |
|||||
1+ Kp |
1+ Kp |
|||||||
f =0 |
|
|
|
|
|
|
|
|
вочной характеристики;
