
5. Спиральность
Если вероятности различных направлений спина одинаковы (спины частиц ориентированы произвольно), то говорят о равной нулю поляризации частиц. Если спины направлены в одну сторону, то говорят о единичной (или стопроцентной) поляризации, и, если спин перпендикулярен импульсу, говорят о поперечной поляризации. Продольная (круговая) поляризация означает, что спин частицы направлен вдоль е¸ импульса (рис.12.9).

Правополяризованной считается частица, спин которой направлен по импульсу, левополяризованной - против импульса (говорят о правой и левой спиральности). Спиральность h определяется как
 . (12.22)
. (12.22)
Правополяризованная частица имеет положительную спиральность (h=+1), левополяризованная - отрицательную (h=-1).
В 1958 г. экспериментально было показано, что спиральность нейтрино всегда отрицательна (h=-1) или нейтрино всегда имеет левую спиральность, а антинейтрино - всегда правую (рис.12.10). Это явилось еще одним доказательством отсутствия инвариантности к пространственной инверсии в слабых взаимодействиях. Нейтрино и антинейтрино, которые появляются и участвуют только в слабых процессах, - постоянные доказательства несохранения четности в слабых взаимодействиях, причем в данном случае четность не сохраняется стопроцентно.

Рис.12.10. Импульс, спиральность и спин антинейтрино и нейтрино
Остановимся
на этом более подробно. Если не принимать
в расчет лептонное квантовое число Le,
то левая часть рис.12.10 (антинейтрино)
связана с правой частью (нейтрино)
операцией зеркального отражения.
Инвариантность к такой операции означает,
что если существует частица (в данном
случае
 ),
у которой направления спина
),
у которой направления спина и импульса
и импульса совпадают,
то должна существовать и зеркально
отображенная частица, у которой спин
противоположен импульсу. Поскольку
пространственная инверсия не меняет
лептонного квантового числа Le,
то у этой зеркально отображенной частицы
Le
должно быть -1, как и у
совпадают,
то должна существовать и зеркально
отображенная частица, у которой спин
противоположен импульсу. Поскольку
пространственная инверсия не меняет
лептонного квантового числа Le,
то у этой зеркально отображенной частицы
Le
должно быть -1, как и у
 .
Т.е. наряду с антинейтрино, у которого
.
Т.е. наряду с антинейтрино, у которого
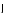 è
è направлены
в одну сторону, должно было бы существовать
и антинейтрино с противоположно
направленными
направлены
в одну сторону, должно было бы существовать
и антинейтрино с противоположно
направленными
 è
è
 .
Так как антинейтрино с такими свойствами
нет, то зеркальная симметрия в
рассматриваемом примере отсутствует.
.
Так как антинейтрино с такими свойствами
нет, то зеркальная симметрия в
рассматриваемом примере отсутствует.
В противоположность этому фотон, который, как и нейтрино, безмассовая частица, движущаяся со скоростью света, существует как в виде левоспиральной, так и в виде правоспиральной частицы (рис.12.11).

Рис.12.11. Импульс, спиральность и спин фотона
Этот факт - прямое следствие сохранения четности в электромагнитных взаимодействиях.
До сих пор мы рассматривали нейтрино и фотон как частицы с продольной поляризацией. Без доказательства сформулируем следующее правило: любая частица с нулевой массой покоя продольнополяризована, т.е. имеет не более двух ориентаций спина - параллельную и антипараллельную е¸ импульсу, независимо от величины спина.
Проще
всего это понять для фотона. Он имеет
спин J=1. Спин частицы (собственный момент
количества движения) можно, хотя и с
оговорками, рассматривать как результат
вращения частицы вокруг собственной
оси симметрии. Для массивной частицы
это выглядит довольно естественно. Но
как интерпретировать такое вращение в
случае такой безмассовой частицы, как
фотон? Единственная возможность -
рассматривать это вращение как вращение
электромагнитного поля (векторов
 è
è ).
Очевидно, для того, чтобы удовлетворить
условию поперечности электромагнитной
волны, вращение должно происходить лишь
вокруг линии импульса (рис.12.12).
).
Очевидно, для того, чтобы удовлетворить
условию поперечности электромагнитной
волны, вращение должно происходить лишь
вокруг линии импульса (рис.12.12).

Ðèñ.12.12
Таким образом, получаем, что спин фотона может иметь лишь две возможные ориентации (+1 и -1). Нулевая проекция спина фотона на направление импульса исключена.
В
1909 г. Пойнтинг предложил эксперимент
для проверки своего предсказания о том,
что электромагнитная волна, поляризованная
по кругу, должна иметь момент количества
движения. Первый успешный эксперимент
такого рода был выполнен в 1935 г. Современный
вариант этого эксперимента - микроволновый
двигатель. Микроволновое излучение,
поляризо-ванное по кругу, падает на
электрический диполь, свободно подвешенный
в конце волновода кругового сечения.
Диполь поглощает энергию волны, получая
момент количества движения, и начинает
вращаться. Зная поглощенную энергию и
частоту вращения, можно определить
собственный момент количества движения
фотона и убедиться, что для фотона
|Jz|= ,
т.е. спин фотона равен 1.
,
т.е. спин фотона равен 1.
Левоспиральность
нейтрино и правоспиральность антинейтрино
можно согласовать с законом сохранения
лептонного заряда лишь в случае их
безмассовости. Такие частицы двигаются
со скоростью света и поэтому в любой
системе координат закрученные, например,
по правому винту частицы остаются
правоспиральными. Для частиц с m 0
можно указать такое преобразование
Лоренца (вдоль импульса), которое изменит
направление импульса на противоположное,
оставив неизменным направление спина
частицы (т.е. направление ее собственного
вращения), и частица, закрученная по
правому винту, превратится в закрученную
по левому винту в новой системе отсчета.
Если бы антинейтрино обладало массой,
то оно могло бы в новой системе отсчета
поменять спиральность на противоположную
и, с этой точки зрения, совпасть с нейтрино
и закон сохранения лептонного заряда
не имел бы места.
0
можно указать такое преобразование
Лоренца (вдоль импульса), которое изменит
направление импульса на противоположное,
оставив неизменным направление спина
частицы (т.е. направление ее собственного
вращения), и частица, закрученная по
правому винту, превратится в закрученную
по левому винту в новой системе отсчета.
Если бы антинейтрино обладало массой,
то оно могло бы в новой системе отсчета
поменять спиральность на противоположную
и, с этой точки зрения, совпасть с нейтрино
и закон сохранения лептонного заряда
не имел бы места.
Мы
уже упоминали в связи с обсуждением
рис.12.10, что операция пространственной
инверсии превращает
 в некий объект, которого нет в природе
- лептонное число антинейтрино (Le=-1),
а спиральность h=-1. Такой спиральностью
обладает e,
íî ó íåãî Le=+1,
à íå -1, êàê ó
в некий объект, которого нет в природе
- лептонное число антинейтрино (Le=-1),
а спиральность h=-1. Такой спиральностью
обладает e,
íî ó íåãî Le=+1,
à íå -1, êàê ó
 .
Пространственная инверсияe
тоже приводит к несуществующему объекту
с Le=+1
и h=+1. Это можно изобразить так
.
Пространственная инверсияe
тоже приводит к несуществующему объекту
с Le=+1
и h=+1. Это можно изобразить так
 , (12.23)
, (12.23)
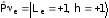 ,
,
где
справа от знака равенства стоят варианты,
не использованные природой. Отсутствие
этих вариантов означает, что e
è
 не имеют определенной внутренней
четности.
не имеют определенной внутренней
четности.
На
изложенных фактах базируется теория
двухкомпонентного (дираковского)
нейтрино. Это же применимо к (h=-1) и
 (h=+1), а также к (h=-1) и
(h=+1), а также к (h=-1) и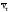 (h=+1). Экспериментально установлено, что
e-,
e;
-,
è -,
в слабых процессах с заряженными
слабыми токами рождаются левополяризованными,
а их античастицы (e+,
(h=+1). Экспериментально установлено, что
e-,
e;
-,
è -,
в слабых процессах с заряженными
слабыми токами рождаются левополяризованными,
а их античастицы (e+,
 ;+,
;+,
 è+,
è+,
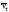 )
- правополяризованными с поляризацией
v/c, т.е. всегда рождается левополяризованным,
а
)
- правополяризованными с поляризацией
v/c, т.е. всегда рождается левополяризованным,
а правополяризованным.
правополяризованным.
