Основные характеристики амплитудного модулятора.Основными характеристиками амплитудного модулятора являются:

• статическая модуляционная,

• динамическая модуляционная,

• частотная.

Статическая модуляционная характеристикапредставляет собой зависимость первой гармоники тока через нелинейный элементI₁или пропорционального ему напряжения на контуреU_кот напряжения смещенияЕ при постоянной амплитуде напряжения возбужденияU_ωна резонансной частотеω_о и при отсутствии напряжения модуляцииU_Ω = 0:

I₁ = f (Е); U_ω = const, ω = ω₀ , U_Ω = 0 . (24.3)

Типичные характеристики для трех значений напряжения возбужденияпоказаны на рис. 24.6. При дальнейшем уве­личении напряжения возбужде­ния характеристики смещаются влево. Наиболее глубокую и ка­чественную модуляцию можно обеспечить, если статическая модуляционная характеристика имеет большую крутизну и бо­лее протяженный линейный участок. Поэтому, выбрав среди характеристик внешнюю (), отметим точками «1, 3» границы линейного ее участка и точкой «2» его середину. Точка «2» при этом соответствует правильному выбору смещенияE₀, а горизонтальные проекции точек «1» и «3» определяют удвоенную максимально допустимую амплитуду модули­рующего напряжения. На выбранном линейном участке между модули­рующим напряжениеми амплитудой напряжения на контуре име­ется линейная зависимость, что должно обеспечить отсутствие нелинейных искажений при модуляции. Наибольшая возможная глубина линейной моду­ляции, достижимая в данном устройстве, может быть рассчитана после оп­ределения параметровина основании (24.2) и в соответствии с рис. 24.6:

= (U_{к mах} – U_{к min}) / (U_{к mах} + U_{к min}). (24.4)

Для того чтобы учесть реальные возможности амплитудного модулятора, необходимо знать две других его характеристики – динамическую и частотную.

Динамической модуляционной характеристикой модулятора(рис. 24.7) называют зависимость коэффициента модуляцииМот амплитуды модулирующего напряжения:М=f (U_Ω) , снятую на резонансной частотеω₀при постоянном напряжении возбуждения, постоянном смещенииE₀и при постоянной частоте модулирующего сигналаF, обычноF= 1 000 Гц.

Как видно из рис. 24.7, характеристика линейна до. При бóльших модулирующих сигналах возникают искажения, связанные с нарушением линейной зависимости амплитудыu_к модулированного колебания от амплитуды сигнала,что при детектировании такого колебания приведет к нелинейным искажениям.

Частотная характеристика модулятора(рис. 24.8) показывает зависимость коэффициента модуляцииMот частоты модулирующего напряженияF: при постоянных значениях E₀, ,иf = f_рез = f₀ .

В реальных условиях модуляция осуществляется сигналом, обладающим определенной шириной спектра и прикладываемым к НЭ через цепи, имеющие неравномерные амплитудно-частотные характеристики. Нагрузка НЭ также является частотно-зависимой. В связи с этим частотная характеристика модулятора зависит от частоты модуляции.

Рассмотрим влияние параллельного колебательного контура в цепи нагрузки НЭ (рис.24.4). Полезными продуктами в спектре тока НЭ являются несущая частота₀ и две боковые (₀ –  ) и (₀ + ). Коэффициент модуляции тока неизменен и не зависит от частоты модуляции. Контур настраивается на частоту₀ , и для этой частоты сопротивление контура максимально. Для боковых частот тока, отстоящих от несущей на , модуль сопротивления контура из за высокой избирательности падает, причем тем больше, чем больше частота модуляции. Соответственно падает и коэффициент модуляции выходного напряжения. Эта составляющая частотной характеристики модулятора может быть рассчитана. Она совпадает по форме с правой ветвью резонансной характеристики контура (см. рис. 24.8) и описывается выражением:

, (24.5)

где M₀– значение глубины модуляции тока, не зависящее от частоты модуляции;

 f_0,7– полоса пропускания колебательного контура.

Для того, чтобы частотные искажения не превысили допустимых, полоса пропускания колебательной системы модулятора f_0,7должна быть не ỳже удвоенной ширины спектра модулирующего сигналаF_m:

 f_0,7.

Базовый амплитудный модулятор. Электрическая схема базового амплитудного модулятора показана на рис. 24.9. Название устройства определено тем, что несущее колебаниеU_н и модулирующий сигнал U_Ω вво­дятся в базовую цепь транзистора VT. Необходимое смещение Е₀ создается делителем напряжения в цепи базы R₁ и R₂. Для суммирования напряжений U_н и U_Ω в базовой цепи точка 2 схемы (рис. 24.9) блокируется конденсатором большой емкости C₂ (по низкой частоте), точка 1 – конденсатором меньшей емкости C₁ (по высокой частоте). Низкочастотный модулирующий сигнал вводится с помощью трансформатора с железным сердечником ТV. Элементы R_ф ,С_ф выполняют роль фильтра в цепи питания. Настроенный на частоту f₀ колебательный контур L, C частично включен в цепь коллектора транзистора и фильтрует полезные составляющие спектра тока транзистора – несущую и пару боковых (см. рис. 24.5). Амплитудно-модулированные колебания (АМК) снимаются на выход с помощью высокочастотного трансформатора.

Балансный амплитудный модулятор.Балансно-модулированным колебанием (БМК) называется ампли­тудно-модулирован­ное колебание, в ко­тором отсутствует со­ставляющая несущей частоты. При тональ­ной амплитудной мо­дуляции БМК опреде­ляется выражением:

u (t) = М U_н cos Ω t cos ω₀ t =

= 0,5 М U_н cos (ω₀ + Ω) t + 0,5 М U_н cos (ω₀ – Ω) t . (24.6)

Д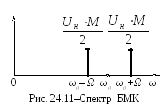иодная схема балансного амплитудного модулятора приведена на рис. 24.10. При полной идентичности плеч модулятора и при квадратичной аппроксимации ВАХ диодовVD1 иVD2 результирующий ток через первичную обмотку выходного трансформатора содержит слагаемое, пропорциональное произведениюu₀ (t) иu_Ω (t) и не содержит слагаемого на несущей частотеω₀ . Спектр БМК соответствует выражению (24.6) и показан на рис. 24.11.

Применение БМК позволяет улучшить энергетические показатели канала связи за счет отсутствия в спектре колебания несущей, не содержащей информации, но обладающей значительной долей мощности в составе амплитудно-модулированного колебания. Ширина спектра БМК, как и в случае обычной амплитудной модуляции (см. рис. 24.3), остается равной удвоенной ширине спектра модулирующего колебания.

Однополосная амплитудная модуляция.Дальнейшее улучшение энергетических показателей канала связи, а также сужение полосы занимаемых им в эфире частот до ширины спектра модулирующего колебания достигается при применении однополосной модуляции.

Структурная схема однополосного модулятора показана на рис. 24.12. На входы подаются несущее

u₀ (t) = U_н cos ω₀ t

и модулирующее

u_Ω (t) = U_Ω cos Ω t

колебания. С учетом сдвига фаз на 90^º напряжения на выходах балансных модуляторов БМ1 и БМ2 соответственно равны (24.6):

u_БМ1(t) = М U_н cos Ω t sin ω₀ t ,

u_БМ2(t) = М U_н sin Ω t cos ω₀ t .

Напряжение на выходе сумматора Σ

u (t) = М U_н sin (ω₀ + Ω) t

является верхней боковой частотой спектра модулированного колебания. Спектр сигнала с однополосной тональной модуляцией показан на рис. 24.13.