1.6. Некоторые понятия теории графов

Ориентированные графы

Определение.

Неупорядоченный ориентированный граф G– это пара (A, R):

A– множество элементов, называемых вершинами;

R– отношения на множествеА.

Пример:

G=(A, R),A={1, 2, 3, 4},R={(1, 1), (1, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 3)} (рис. 1.7).

Рис. 1.7. Пример ориентированного графа

Пара (a, b) – называется дугой (или ребром) графаG.

Определение.

Пусть G₁=(A₁, R₁)иG₂=(A₂, R₂) -G₁ и G₂ равные (изоморфные), если существует биективное отображениеf:A₁A₂ такое, чтоaR₁bтогда и только тогда, когдаf(a)R₂f(b), т.е. в графеG₁из вершиныав вершинуbведет дуга тогда и только тогда, когда в графеG₂из вершины, соответствующейа, ведет дуга, соответствующая вершинеb.

Части вершинам и/или дугам графа иногда приписывают некоторую информацию (разметку). Такие графы называются помеченными.

Определение.

(A, R) – граф. Разметкой графа называется пара функцийfиg, гдеf(разметка вершины) отображаетАв некоторое множество, аg(разметка дуг) отображаетRв некоторое (возможно отличное от первого) множество.

Пусть G₁=(А₁, R₁)иG₂=(А₂, R₂) – равные помеченные графы, если существует такое биективное отображениеh: A₁,….,A_n,что:

1. aR₁bтогда и только тогда, когдаh(a)R₂h(b), т.е. графы равны как непомеченные;

2. f₁(a)=f₂(h(a)), т.е. соответствующие вершины имеют одинаковые метки;

3. g₁((a,b))=g₂((h(a), h(b))), т.е. соответствующие дуги имеют одинаковые метки.

Пример.G₁={{a, b, c}{(a, b), (b, c), (c, a)}} иG₂={{0, 1, 2}{(1, 0), (2, 1), (0, 2)}} (рис. 1.8).

Разметка графа G₁определяется формулами:

Разметка графа G₂определяется формулами

Графы равны.

Определение.

Последовательность вершин (а₀,а₁, …,а_n), n1 называется путем длиныnиз вершиныа₀в вершинуа_n, если для каждого 1i nсуществует дуга, выходящая иза_i-1 и входящая в вершинуа_i.

Циклом называется путь (а₀, а₁, …, а_n), в которома₀ = а_n .

Граф называется сильно связанным, если для двух различных вершин aиbсуществует путь изавb.

Степенью по входувершиныаназовем число входящих в нее дуг, степенью по выходу– число выходящих из нее дуг.

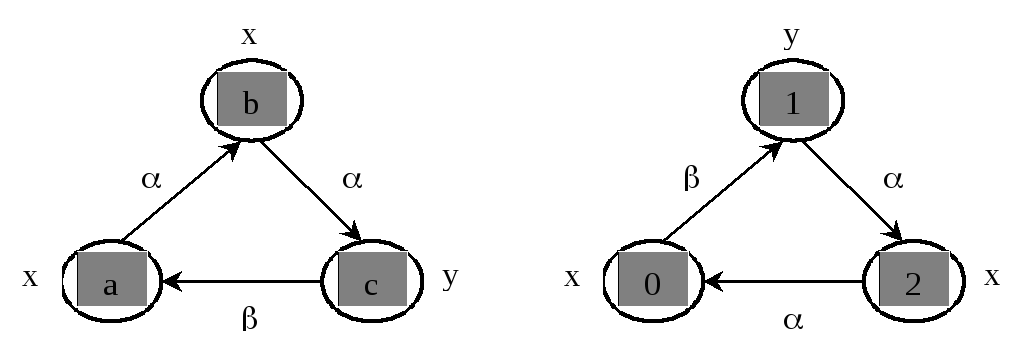
Рис. 1.8. Равные помеченные графы

Ориентированные ациклические графы

Ациклическим графомназывается граф, не имеющий циклов (рис. 1.9).

Вершина, степень по входу которой 0, называется базовой.

Вершина, степень по выходу которой 0, называется листом(или концевой вершиной).

Если (a, b) – дуги ациклического графа, тоаназывается прямым предкомb, аb – прямым потомкома.

Рис. 1.9. Пример ациклического графа

Деревья

Определение.

Деревом Тназывается ориентированный графG=(A,R) со специальной вершинойrA, называемой корнем, у которого:

1. степень по входу rравна 0;

2. степень по входу всех остальных вершин дерева Травна 1;

3. каждая вершина достижима из r.

Определение.

Поддеревом дерева Т=(A, R) называется любое деревоТ=(A, R), у которого (рис. 1.10):

1. Aне пусто и содержится вА;

2. R=(AA)R;

3. ни одна вершина A - Aне является потомком вершиныA.

Рис. 1.10. Примеры дерева

Упорядоченные графы

Упорядоченным графом называется пара (A, R), гдеА- множество вершин, аR– множество линейно упорядоченных списков дуг, каждый элемент которого имеет вид ((a, b₁), (a, b₂),…,(a,b_n)) (рис. 1.11).

Этот элемент показывает, что из вершины авыходитnдуг, причем первой из них считается дуга, приходящая вb₁ , второй - вb₂ и т.д.

Разметкой упорядоченного графаG=(A, R) назовем такую пару функцийf иg, что:

1. f:ASдля некоторого множестваS (fпомечает вершины);

2. gотображаетR в последовательность символов из некоторого множества Ттак, что образом списка ((a, b)). ((a, b)) является последовательность изn символов (помеченные дуги).

Рис. 1.11. Упорядоченный граф

Контрольные вопросы

1. Операции над множествами.

2. Отношения.

3. Замыкание отношений.

4. Отношения порядка.

5. Отображения.

6. Множества цепочек.

7. Операции над цепочками.

8. Языки.

9. Операции над языками.

10. Итерация языка.

11. Гомоморфизм.

12. Алгоритмы.

13. Частичные алгоритмы.

14. Полные алгоритмы.

15. Рекурсивные алгоритмы.

16. Задание алгоритмов.

17. Ориентированные графы.

18. Ориентированные ациклические графы.

19. Деревья. Упорядоченные графы.