
- •Теория вычислительных процессов и структур
- •1. Предварительные математические сведения
- •1.2. Операции над множествами Объединение множеств
- •Пересечение множеств
- •Разность множеств
- •1.3. Множества цепочек
- •1.4. Языки
- •1.5. Алгоритмы
- •1.6. Некоторые понятия теории графов
- •2. Введение в компиляцию
- •2.1. Задание языков программирования
- •2.2. Синтаксис и семантика
- •2.3. Процесс компиляции
- •2.4. Лексический анализ
- •2.5. Работа с таблицами
- •2.6. Синтаксический анализ
- •2.7. Генератор кода
- •Алгоритм.
- •2.8. Оптимизация кода
- •2.9. Исправление ошибок
- •2.10. Резюме
- •3. Теория языков
- •3.1. Способы определения языков
- •3.2. Грамматики
- •Пример.
- •3.3. Грамматики с ограничениями на правила
- •3.4. Распознаватели
- •3.5. Регулярные множества, их распознавание
- •3.6. Регулярные множества и конечные автоматы
- •3.7. Графическое представление конечных автоматов
- •3.8. Конечные автоматы и регулярные множества
- •3.9. Минимизация конечных автоматов
- •3.10. Контекстно-свободные языки
- •3.10.1. Деревья выводов
- •3.10.2. Преобразование кс–грамматик
- •3.10.3. Грамматика без циклов
- •3.10.4. Нормальная форма Хомского
- •3.10.5. Нормальная формула Грейбах
- •3.11. Автоматы с магазинной памятью
- •3.11.1. Основные определения
- •3.11.2. Эквивалентность мп-автоматов и кс-грамматик
- •4.1. Эквивалентность мп-автоматов и кс-грамматик
- •4.2. Ll(1)-грамматики
- •4.3. Ll(1)-таблица разбора
- •5. Синтаксический анализ снизу вверх
- •5.1. Разбор снизу вверх
- •5.2. Lr(1) - таблица разбора
- •5.3. Построение lr – таблицы разбора
- •5.4. Сравнение ll – и lr – методов разбора
- •6. Включение действий в синтаксис
- •6.1. Получение четверок
- •6.2. Работа с таблицей символов
- •7. Проектирование компиляторов
- •7.1. Число проходов
- •7.2. Таблицы символов
- •Identifier, type.
- •Int procedure rehash(int n)
- •Int procedure rehash(int n)
- •7.3. Таблица видов
- •8. Распределение памяти
- •8.1. Стек времени прогона
- •Integer a, b, X, y
- •Int table[1:10, -5:5].
- •8.2. Методы вызова параметров
- •8.3. Обстановка выполнения процедур
- •8.4. «Куча»
- •8.5. Счетчик ссылок
- •8.6. Сборка мусора
- •9. Генерация кода
- •(Тип – адреса, номер - блока, смещение).
- •9.2. Структура данных для генерации кода
- •9.3. Генерация кода для типичных конструкций
- •9.3.1. Присвоение
- •9.3.2. Условные зависимости
- •If b then c else d
- •9.3.3. Описание идентификаторов
- •9.3.4. Циклы
- •9.3.5. Вход и выход из блока
- •9.3.6. Прикладные реализации
- •9.4. Проблемы, связанные с типами
- •9.5. Время компиляции и время прогона
- •10. Исправление и диагностика ошибок
- •10.1. Типы ошибок
- •10.2. Лексические ошибки
- •10.3. Ошибки в употреблении скобок
- •Begin end
- •Case esac
- •10.4. Синтаксические ошибки
- •10.5. Методы исправления синтаксических ошибок
- •End begin
- •10.6. Предупреждения
- •10.7. Сообщения о синтаксических ошибках
- •10.8. Контекстно-зависимые ошибки
- •Identifier xyz not declared
- •Identifier blank alredy declared in block
- •10.9. Ошибки, связанные с употреблением типов
- •Int I; char c;
- •10.10. Ошибки, допускаемые во время прогона
- •10.11. Ошибки, связанные с нарушением ограничений
1.3. Множества цепочек
Алфавитомбудем называть любое множество символов (оно не обязательно конечно и даже счетно), но в наших приложениях оно конечно. Предполагается, что слово «символ» имеет достаточно ясный интуитивный смысл.
Символ – (синонимы: буква, знак) элемент алфавита.
Пример:
01011 – цепочка в бинарном алфавите {0, 1}.
Особый вид цепочки – пустая цепочка, обозначается e. Пустая цепочка не содержит символов.
Соглашение.
Прописные буквы греческого алфавита – алфавиты.
a, b, c иd– отдельные символы.
t, u, v, w, x, y и z– цепочка символов.
Если цепочку из iсимволов обозначитьa![]() ,тогда a0=e – пустая
цепочка.
,тогда a0=e – пустая
цепочка.
Определение:
Цепочки в алфавите определяются следующим образом:
е– цепочка в;
если xцепочка виа, тоxa – цепочка в;
y– цепочка втогда и только тогда, когда она является таковой в силу 1) и 2).
Операции над цепочками
Пусть x, y– цепочки.
Цепочка xy– называется сцепленной (конкатенацией). Например,x=ab;y=cd;xy=abcd. Для любой цепочкиx xе=еx=x.
Обращением цепочки x
 называется цепочкаx, записанная
в обратном порядке:
называется цепочкаx, записанная
в обратном порядке:
 ,
,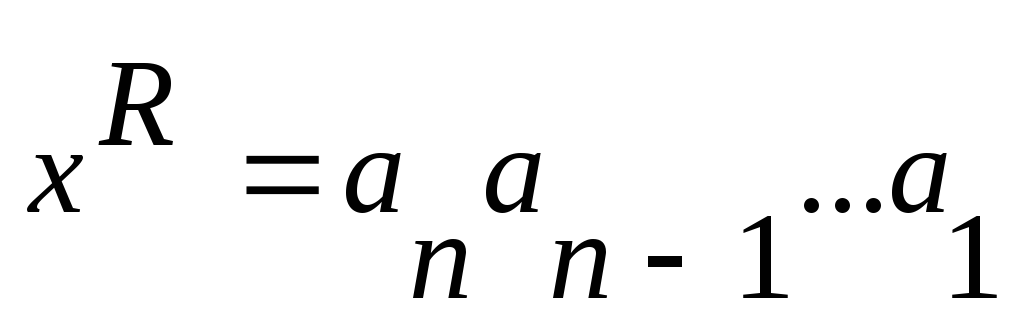 ,
, .
.Пусть x, y, z– цепочки в некотором алфавите, тогда:
x– префикс цепочкиxy;
y– суффикс цепочкиxy;
y– называется подцепочкой цепочкиxyz.
Префикс и суффикс цепочки являются ее подцепочками.
Если xy, x – префикс (суффикс) цепочкиy, тоx- собственный префикс (суффикс) цепочкиy.
Длина цепочки –
это число символов в ней. Если
![]() ,
то длина цепочкиn. Длину цепочки
обозначают|x|, например|abc|=3;|e|=0.
,
то длина цепочкиn. Длину цепочки
обозначают|x|, например|abc|=3;|e|=0.
1.4. Языки
Языком в алфавите называют множество цепочек в.
Определение.
Через *обозначается множество, содержащее все цепочки в алфавите, включаяе.
Например.- бинарный алфавит {0,1}, тогда*={e, 0, 1, 00, 01, 10, 11, 000, …,}.
Каждый язык в алфавите является подмножеством*. Множество всех цепочек в, за исключениеме, обозначают+.
Определение. Если языкLтаков, что полная цепочка вLне является собственным подмножеством (суффиксом) никакой другой цепочки вL, тоLобладает префиксным (суффиксным) свойством.
Операции над языком
Так как языки являются множествами, то все операции над множествами применимы к ним. Операцию конкатенации можно применять к языкам так же, как и к цепочкам.
Определение.
Пусть L1язык в1.,
L2язык в2.
Тогда языкL1L2называется конкатенацией языковL1
иL2 - это язык
![]() .Итерация языкаLобозначаетсяL*,
определяется:
.Итерация языкаLобозначаетсяL*,
определяется:
L0={e};
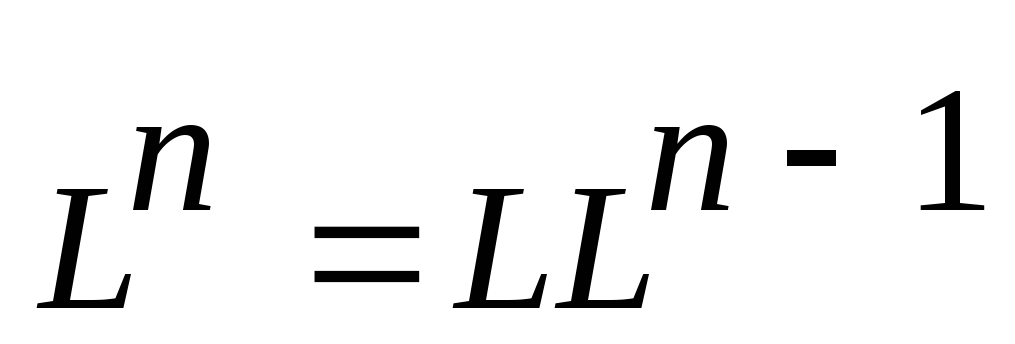 для
n1;
для
n1; .
.
Позитивная
итерация языка L
обозначается L+
- это язык
![]() ,
т.е.
,
т.е.
![]()
Определение.
Пусть 1 и 2 - алфавиты. Гомоморфизмом называется любое отображение h: 1 *2.
Область
гомоморфизма можно расширить до
![]() полагаяh(e)=e
и h(xa)=h(x)h(a)
для всех x
полагаяh(e)=e
и h(xa)=h(x)h(a)
для всех x![]() ,
и а
,
и а![]() .
.
Пример.
Если
мы хотим заменить каждое вхождение в
цепочку символа 0 на а,
а каждое вхождение символа 1 на bb,
то можно определить гомоморфизм h
так: h(0)=a,
h(1)=bb. Если
![]() ,
то
,
то![]() .
.
Определение.
Если
h: 1
![]() ,
то отношениеh-1:
,
то отношениеh-1:
![]()
P(
P(![]() )
называется обращением гомоморфизма.
)
называется обращением гомоморфизма.
Если
y![]() ,
тоh-1(y)
– это множество цепочек в алфавите 1,
т.е.
,
тоh-1(y)
– это множество цепочек в алфавите 1,
т.е.
![]() .
ЕслиL
– язык в алфавите 2,
то
.
ЕслиL
– язык в алфавите 2,
то
![]() - язык в алфавите
- язык в алфавите![]() состоящий из тех же цепочек, которыеh
отображает в цепочки из L.
Формально
состоящий из тех же цепочек, которыеh
отображает в цепочки из L.
Формально
![]()
Пример.
h – гомоморфизм h(0)=a и h(1)=а, тогда
![]()
