3.11.2. Эквивалентность мп-автоматов и кс-грамматик

В теории перевода можно показать, что языки определяемые МП-автоматами, – это в точности КС-языки. Начнем с построения естественного (недетерминированного) «нисходящего» распознавателя, эквивалентного данной КС-грамматике.

Лемма.

Пусть - КС-грамматика. По грамматике G можно построить такой МП-автомат R, что .

Доказательство.

Построим R так, чтобы он моделировал все левые выводы в G.

Пусть , где  определяется следующим образом:

1. если А  а принадлежит Р, то содержит ;

2. для всех .

Мы хотим показать, что тогда и только тогда, когда ⊢ⁿ для некоторых .

Необходимость этого условия докажем индукцией по m. Допустим, что . Если m=1 и , то

⊢ ⊢^k.

Теперь предположим, что для некоторого m>1. Первый шаг этого вывода должен иметь вид , где для некоторого и . Тогда ⊢ . Если , то по предложению индукции ⊢^*.

Если , то ⊢ . Объединяя вместе эти последовательности тактов, видим, что ⊢⁺ .

Для доказательства достаточности покажем индукцией по n, что, если ⊢ⁿ , то .

Если n=1, то w=e и Ae принадлежит Р. Предположим, что утверждение верно для всех . Тогда первый такт, сделанный МП-автоматом R, должен иметь вид ⊢ , причем ⊢ⁿ_i для и . Тогда - правило из Р, и по предложению индукции для . Если , то . Таким образом

- вывод цепочки w из А в грамматике G.

Контрольные вопросы

1. Способы определения языков.

2. Грамматики.

3. Грамматики с ограничениями на правила.

4. Распознаватели.

5. Регулярные множества, их распознавание и порождения.

6. Алгоритм решения системы линейных выражений с регулярными выражениями.

7. Регулярные множества и конечные автоматы.

8. Проблема разрешимости.

9. Графическое представление конечных автоматов.

10. Минимизация конечных автоматов.

11. Алгоритм построения канонического конечного автомата. Контекстно-свободные грамматики.

12. Деревья выводов. Преобразование КС-грамматик.

13. Алгоритм устранения недостижимых символов.

14. Алгоритм устранения бесполезных символов.

15. Алгоритм преобразования в грамматику без е-правил. Алгоритм устранения цепных правил.

16. Грамматики без циклов. Нормальная форма Хомского. Алгоритм преобразования к нормальной форме Хомского.

17. Нормальная форма Грейбах.

18. Алгоритм устранения левой рекурсии.

19. Автоматы с магазинной памятью.

4. КС-грамматики и синтаксический анализ сверху вниз

4.1. Эквивалентность мп-автоматов и кс-грамматик

В практических приложениях нас больше будут интересовать детерминированные МП-автоматы, т.е. такие, которые в каждой конфигурации могут сделать не более одного очередного такта. Языки, определяемые детерминированными МП-автоматами, называются детерминированными КС-языками, а их грамматики - LR(k)-грамматиками.

Определение.

МП-автомат называется детерминированным (ДМП), если для каждых и либо

1. содержит не более одного элемента для каждого и , либо

2. для всех и 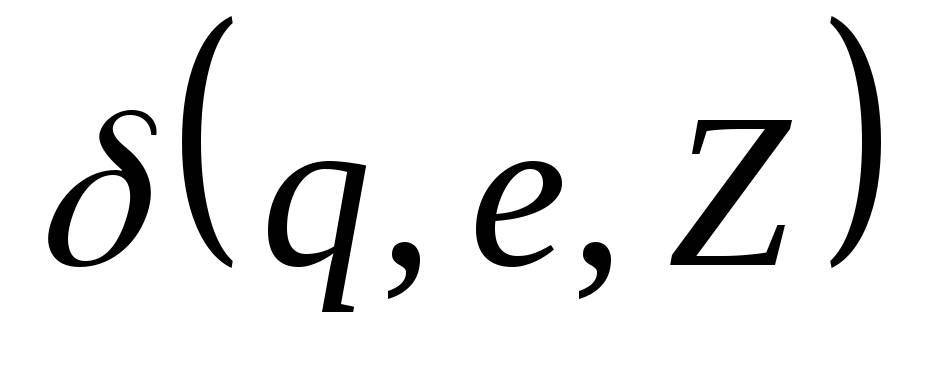содержит не более одного элемента.

Соглашение. Так как ДМП-автомат содержит не более одного элемента, мы будем писать вместо .

Как уже отмечалось, однотактовые детерминированные МП-автоматы порождают КС-языки, которые называются LR(k)-грамматиками. Те в свою очередь являются частным случаем s-грамматик.

Определение. s-грамматика представляет собой грамматику, в которой:

1. правые части каждого порождающего правила начинаются с терминала;

2. в тех случаях, когда в левой части более чем одного порождающего правила появляется нетерминал, соответствующие правые части начинаются с различных терминалов.

Первое условие аналогично утверждению, что грамматика находится в нормальной форме Грейбах, только за терминалом в начале каждой правой части правила могут следовать нетерминалы и/или терминалы.

Второе условие соответствует существованию детерминированного одношагового МП-автомата.

Пример.

SpX SqY XaXb

Xx YaYd Yy

Рассмотрим проблему разбора строки paaaxbbb с помощью заданной s-грамматики. Начав с символа S, попытаемся генерировать строку, применяя левосторонний вывод. Результаты приведены в табл. 4.1.

Таблица 4.1.

Исходная строка	Вывод
paaaxbbb paaaxbbb paaaxbbb paaaxbbb paaaxbbb paaaxbbb	S PX PaXb PaaXbb PaaaXbbb Paaaxbbb