3.10.3. Грамматика без циклов

Определение.

КС – грамматика G = (N,  Р S) называется грамматикой без циклов, если в ней нет вывода А ⁺ А для АN. Грамматика называется приведённой, если она без циклов, без е – правил и без бесполезных символов.

Большинство (если не все) языки программирования обладают именно этими свойствами.

3.10.4. Нормальная форма Хомского

Определение. КС–грамматика G = (N,  Р S) называется грамматикой в нормальной форме Хомского (или бинарной нормальной форме), если каждое правило из Р имеет один из следующих видов:

1. А  ВС, где А, В, С принадлежит N;

2. А  а, где а;

3. S  е, если еL(G), причём S не встречается в правых частях правил.

На практике каждый КС – язык порождается грамматикой в нормальной форме Хомского. Это очень полезно, когда требуется простая форма представления КС – языка.

Алгоритм преобразования к нормальной форме Хомского.

Вход. КС–грамматика G = (N,  Р S).

Выход. Эквивалентная КС-грамматика G' в нормальной форме Хомского, т.е. L(G')=L(G).

Метод. Грамматика G' строится следующим образом.

1. Включить в Р' каждое правило из Р вида А а.

2. Включить в Р' каждое правило из Р вида А ВС.

3. включить в Р' каждое правило Sе, если оно было в Р.

4. для каждого правила из Р вида , где k >2, включить в Р' правила

…………………………………

,

где , если ; – новый нетерминал, если ; - новый терминал.

5. Для каждого правила из Р вида , где хотя бы один из символов и принадлежит , включить в Р' правило .

6. Для каждого нетерминала вида а', введённого на шагах 4) и 5), включить в Р' правило а'а. Наконец, пусть N' – это N вместе со всеми нетерминалами, введёнными при построении Р'. Тогда искомая грамматика G' = (N', ' Р' S).

Пример.

Пусть G – приведённая грамматика, определённая правилами

S  аАВ | ВА

А  ВВВ | а

В  АS | b.

Строим Р' рассмотренным выше алгоритмом, сохраняя правила SВА, A а, В  АS и В  b. Заменяем правило S  аАВ на S  а'<AB> и <АВ>  АВ, а А  ВВВ – правилами A В<BB> и <BB>BB. Наконец, добавляем а'а. В результате получим грамматику G'= (N', {a, b}, Р', S) и Р' состоит из правил:

S  а'<АВ> | BA

А  В<BB> | a

B  AS | b

<AB>  AB

<BB>  BB

a'  а.

3.10.5. Нормальная формула Грейбах

Очень важно для языков программирования использовать грамматику, в которой все правые части правил начинаются с терминалов. Построение таких грамматик связано с устранением любой рекурсии.

Определение.

Нетерминал А в КС–грамматике G = (N,  Р S) называется рекурсивным, если А⁺ A для некоторых  и . Если  = е, то А называется леворекурсивным. Аналогично, если  = е, то А называется праворекурсивным. Грамматика, имеющая хотя бы один леворекурсивный терминал, называется леворекурсивной. Аналогично определяется и праворекурсивная грамматика. Грамматика, в которой все не терминалы, кроме может быть начального символа, рекурсивные называется рекурсивной грамматикой.

Практически все языки программирования определяются нелеворекурсивной грамматикой. Поэтому все элементы левой рекурсии должны быть устранены из грамматики.

Лемма.

Пусть G = (N,  Р S) – КС–грамматика, в которой

- все правила из Р и ни одна из цепочек не начинается с А.

Пусть G'=(N{A'}, , P', S), где А' – новый терминал, а Р' получено из Р заменой А – правил правилами

.

Тогда L(G')=L(G).

Рассмотрим на графе, как это реализуется (рис. 3.10).

а) б)

Рис 3.10. Праволинейная а) и леволинейная б) грамматики

Пример:

Пусть G₀ наша обычная грамматика с правилами:

ЕE+T | T

TT*F | F

F(Е)  a.

Применяя к ней вышерассмотренную лемму, получаем эквивалентную грамматику с правилами:

Е Т | TE'

E' +T | + TE'

Т F | FT'

Т'*F | * FT'

F (Е) | a.

На основании вышеописанного построим алгоритм устранения левой рекурсии. Он будет подобен алгоритму решения уравнения с размерными коэффициентами.

Алгоритм устранения левой рекурсии.

Вход. Приведённая КС–грамматика G = (N,  Р S).

Выход. Эквивалентная КС-грамматика без левой рекурсии.

Метод.

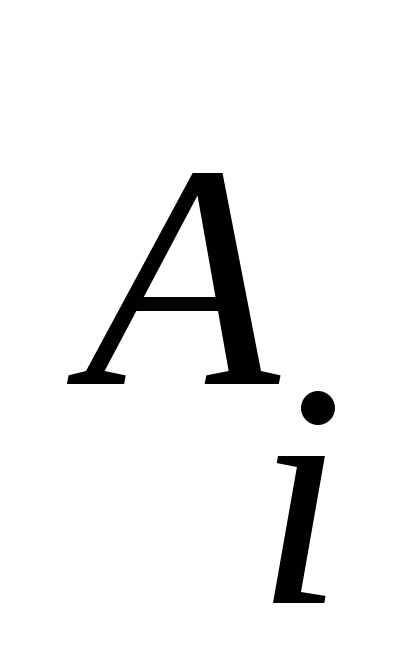
1. Пусть . Преобразуем G так, чтобы в правиле  цепочка  начиналась либо с терминала, либо с такого , что i>j. С этой целью положим i=1.

2. Пусть множество , где ни одна из цепочек не начинается с , если ki заменим – правила правилами:

,

где – новый нетерминал. Правые части всех – правил начинаются теперь с терминала или с , для которого k>i.

3. Если i=n, то полученную грамматику считаем результатом и останавливаемся, в противном случае i=i+1 и j=1.

4. Заменим каждое правило правилами , где для всех - правил. Так как правая часть каждого правила начинается уже с терминала или для к>j, то правая часть каждого - правила будет теперь обладать этими свойствами.

5. Если j=i-1, перейти к шагу 2), в противном случае положить i=i+1 и перейти к шагу 4).

На основании вышесказанного можно однозначно доказать теорему, что каждый КС-язык определяется нелеворекурсивной грамматикой.

Определение.

КС-грамматика G = (N,  Р S) называется грамматикой в форме Грейбах, если в ней нет е- правил и каждое правило из Р, отличное от Se, имеет вид Аa, где а, N^*.