3.10.2. Преобразование кс–грамматик

КС-грамматику часто требуется модифицировать так, чтобы порождаемые ею языки приобрели нужную структуру. Рассмотрим, например, язык L(G₀). Этот язык порождается грамматикой G с правилами

ЕЕ+Е | Е*Е | (Е) | a.

Но эта грамматика имеет два недостатка. Прежде всего, она неоднозначна из-за наличия правила ЕЕ+Е | Е*Е. Эту неоднозначность можно устранить, взяв вместо G грамматику G₁ с правилами

ЕЕ+Т | Е*Т | Т

Т(Е) | а.

Другой недостаток грамматики G, которым обладает и грамматика G₁, заключается в том, что операции + и * имеют один и тот же приоритет, т.е. структура выражения а+а*а и а*а+а, которую мы придаём грамматике G₁, подразумевает тот же порядок выполнения операций, что и в выражениях (а+а)*а и (а*а)+а соответственно.

Чтобы получить обычный приоритет операций + и *, при которых * предшествует + и выражение а+(а*а) понимается как а+(а*а), надо перейти к грамматике G₀.

Общего алгоритмического метода, который придавал бы данному языку произвольную структуру, не существует. Но с помощью ряда преобразований можно видоизменить грамматику, не испортив порождаемый ею язык.

Начнём с очевидных, но важных преобразований. Например, в грамматике G=({S,A}, {a, b}, P, S), где Р={Sa, Ab}, нетерминал А и терминал b не могут появляться ни в какой выводимой цепочке. Таким образом, эти символы не имеют отношения к языку L(G) и их можно устранить из определения грамматики G, не затронув языка L(G).

Определение.

Назовём символ ХN бесполезным в КС – грамматике G = (N,  Р S), если в ней нет вывода вида S^ wXy ^ wxy, где w, x, y принадлежат ^ .

Чтобы установить, бесполезен ли нетерминал А, построим сначала алгоритм, выясняющий, может ли этот нетерминал порождать какие - либо нетерминальные цепочки, т.е. алгоритм, решающий проблему пустоты множества {w | A ^ w, w ^}.

Алгоритм. Непуст ли язык L(G)?

Вход. КС-грамматика G = (N,  Р S).

Выход. «ДА» если L(G), «НЕТ» в противном случае.

Метод. Строим множества рекурсивно.

1. Положить = , i=1.

2. Положить .

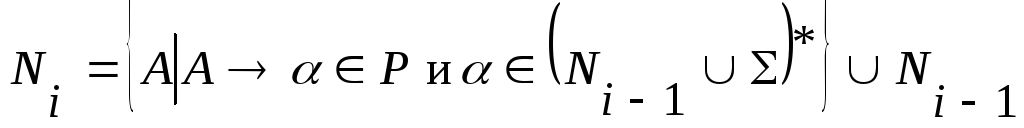3. Если  , то положить i=i+1 и перейти к шагу 2), в противном случае - =.

4. если S, то выдать вывод «ДА», в противном случае – «НЕТ».

Так как символ N, то алгоритм должен остановиться максимум после n+1 повторения шага 2).

Теорема.

Алгоритм, приведённый выше, говорит «ДА» тогда и только тогда, когда S^w для некоторой цепочки w  ^ .

Определение.

Символ XN назовём недостижимым в КС – грамматике G = (N,  Р S), если х не появляется ни в одной выводимой цепочке.

Недостижимые символы можно устранить из КС – грамматики с помощью следующего алгоритма.

Алгоритм устранения недостижимых символов.

Вход. КС – грамматика G = (N,  Р S).

Выход. КС - грамматика G' = (N', ' Р' S), у которой

i) L(G')=L(G),

ii) для всех существуют такие цепочки  и  из (N' ')^*, что S^_G' X.

Метод.

1. Положить = {S} и i=1.

2. Положить .

3. Если , положить i=i+1 и перейти к шагу (2), в противном случае, пусть

• ,

• ,

• Р' – состоит из правил множества Р, содержащих только символы из ,

• G' = (N', ' Р' S).

Заметим, что шаг 2) алгоритма можно повторить только конечное число раз, т.к. .

На базе двух рассмотренных алгоритмов построим обобщенный алгоритм устранения бесполезных символов.

Алгоритм устранения бесполезных символов.

Вход. КС – грамматика G = (N,  Р S), у которой L(G).

Выход. КС - грамматика G' = (N', ' Р' S), у которой L(G')=L(G) и в N' ' нет бесполезных символов.

Метод.

1. Применив к G алгоритм «не пуст ли язык?», получить , положить G₁ = (N, , , S), где состоит из множества правил Р, содержащих только символы из .

2. Применив к G₁ алгоритм «устранение недостижимых символов», получить G' = (N', ' Р' S).

Таким образом, на шаге 1) нашего алгоритма из G устраняются все нетерминалы, которые не могут порождать терминальных цепочек. Затем на шаге 2) устраняются все недостижимые символы.

Каждый символ Х результирующей грамматики должен появиться хотя бы в одном выводе вида S^ wXy ^ wxy.

Резюме. Грамматика G', которую строит рассматриваемый алгоритм, не содержит бесполезных символов.

В практике построения трансляторов обычно правила Ае бессмысленны. Очень полезно отработать метод устранения таких правил из грамматики.

Определение.

Назовём КС – грамматику G = (N,  Р S) грамматикой без е - правил (или неукорачивающей), если либо Р не содержит е – правил, либо есть точно одно правило Sе и S не встречается в правых частях остальных правил из Р.

Алгоритм преобразования в грамматику без е – правил.

Вход. КС – грамматика G = (N,  Р S).

Выход. Эквивалентная КС - грамматика G' = (N', ' Р' S) без е – правил.

Метод.

1. Построить .

2. Построить Р' следующим образом:

a) если принадлежит Р, k и для 1iк, но ни один символ в цепочках (0jk) не принадлежит , то включить в Р' все правила вида:

,

где - либо , либо е, но не включает правило Ае (это могло бы произойти в случае, если все равны е);

б) если S  , включить в Р' правила S'e | S, где S' – новый символ, и положить N'=N{S'}, в противном случае положить N'=N и S'=S.

3. Положить G' = (N', ' Р' S').

Пример.

Рассмотрим грамматику SаSbS | bSaS | e. Применяя к ней рассмотренный алгоритм, получаем грамматику

S'S | e

S аSbS | bSaS | aSb | abS | ab | bSa | baS | ba.

Другое полезное преобразование грамматик – устранение правил вида А  В, которые мы будем называть цепными.

Алгоритм устранения цепных правил.

Вход. КС – грамматика G = (N,  Р S ) без е – правил.

Выход. Эквивалентная КС - грамматика G' = (N', ' Р' S) без е – правил и цепных правил.

Метод.

1. Для каждого АN построить N_А = {B | A ^* В} следующим образом.

а) положить = {A} и i=1;

б) положить ;

в) если , то положить i=i+1 и повторить шаг б), в противном случае положить .

2. Построить Р' следующим образом: если В принадлежит Р и не является цепным правилом, включать в Р' правило А для таких А, что .

3. Положить G' = (N', ' Р' S).

Пример.

Грамматика с правилами

Е  Е+Т | Т

Т  Т * F | F

F  (Е) | a.

Применим к данной грамматике рассмотренный выше алгоритм. На шаге 1) N_Е = {E, T, F}, N_Т = {T, F}, N_F = {F}. После шага 2) множество Р' станет такими:

E  Е+Т | T*F | (E)| a

Т  Т*F | (E) | a

F  (Е) | а.