3.10. Контекстно-свободные языки

Из четырёх классов грамматики иерархии Хомского класс контекстно-свободных языков наиболее важен с точки зрения приложения к языкам программирования и компиляции. С их помощью можно определить большую часть синтаксических структур языков программирования. Кроме того, они служат основой различных схем перевода, т.к. в ходе процесса компиляции синтаксическую структуру, передаваемую входной программе КС-грамматикой, можно использовать при построении перевода этой программы.

Синтаксическую структуру входной цепочки можно определить по последовательности правил, применяемых при выводе этой цепочки. Таким образом, на часть компилятора, называемую синтаксическим анализатором, можно смотреть как на устройство, которое пытается выяснить, существует ли в некоторой фиксированной КС-грамматике вывод входной цепочки.

Естественно, что эта задача нетривиальная – по данной КС-грамматике G и входной цепочке w выяснить, принадлежит ли w языку L(G), и если «да», то найти вывод цепочки w в грамматике G.

3.10.1. Деревья выводов

В грамматике может быть несколько выводов, эквивалентных в том смысле, что во всех них применяются одни и те же правила в одних и тех же местах, но в различном порядке. КС-грамматика позволяет ввести удобное графическое представление класса эквивалентных выводов, называемое деревом выводов.

Определение.

Дерево вывода в КС-грамматике G = (N,  Р S),

где N – конечное множество нетерминальных символов;

 - непересекающееся с N множество терминальных символов;

Р – конечное подмножество множества (N)^N(N)^ (N)^ (элемент ( ) множества Р называется правилом или продукцией );

S – выделенный символ из N, называемый начальным или исходным символом,

- это помеченное упорядоченное дерево, каждая вершина которого помечена символом из множества N{e}.

Если внутренняя вершина помечена символом А, а её прямые потомки - символами , то А – правило грамматики.

Определение.

Помеченное упорядоченное дерево D называется деревом вывода (или деревом разбора) в КС-грамматике G(А) = (N,  Р A), если выполняются следующие условия:

1. корень дерева помечен А;

2. если – поддеревья, над которыми доминируют прямые потомки корня дерева, и корень помечен 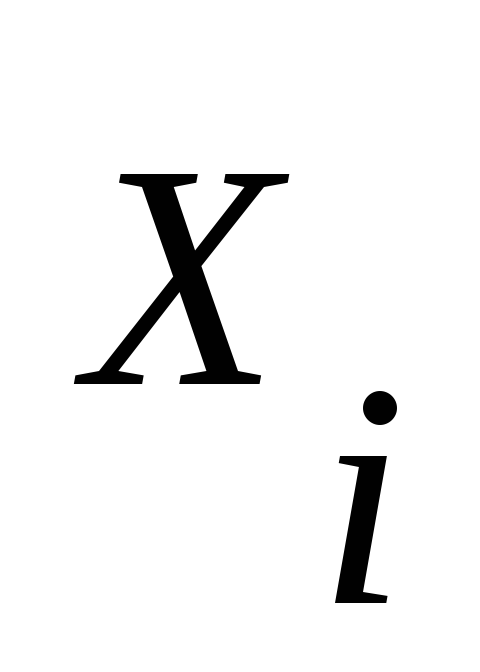, то А – правило из множества Р. должно быть деревом вывода в грамматике G() = (N,  Р ), если – нетерминал, и состоит из единственной вершины, помеченной , если - терминал.

Пример. Имеем грамматику G=G(S) с правилами SaSbS | bSaS | e (рис.3.7).

Рис. 3.7. Деревья выводов

SaSbS | bSaS | e

Заметим, что существует единственное упорядочение вершин упорядоченного дерева, у которого прямые потомки вершины упорядочиваются «слева направо».

Допустим, что n – вершина и – её прямые потомки. Тогда если i<j, то вершина и все её потомки считаются расположенными левее вершины и всех её потомков.

Определение.

Кроной дерева вывода назовём цепочку, которая получится, если выписать слева направо метки листьев.

Кроны наших деревьев: S, е, abab, abab.

Определение.

Сечением дерева D назовём такое множество С вершин дерева D, что

1. никакие две вершины из С не лежат на одном пути в D;

2. ни одну вершину дерева D нельзя добавить к С, не нарушив свойства 1).

Пример.

• Множество вершин дерева, состоящего из одного корня, является сечением.

• Листья также образуют сечение.

Рис. 3.8. Пример сечения дерева

Определение.

Кроной сечения дерева D является цепочка, получаемая конкатенацией (в порядке слева направо) меток вершин, образующих некоторое сечение.

Крона сечения примера, приведенного на рис.3.7, - abaSbS.

Лемма.

Пусть S= – вывод цепочки из S в КС – грамматике G = (N,  Р S). Тогда в G можно построить дерево вывода D, для которого – крона, а – некоторые из крон сечения.

Лемма.

Пусть D – дерево вывода в КС-грамматике G = (N,  Р S) с кроной . Тогда S^ (транзитивное и рефлексивное замыкание ^, т.е.  выводима из S).

Доказательство.

Пусть – такая последовательность сечений дерева D, что

1. С₀ – содержит только один корень дерева D;

2. для 0i<n получается из заменой одной нетерминальной вершины её прямыми потомками;

3. – крона дерева D.

Ясно, что хотя бы одна такая последовательность существует.

Если – крона сечения , то существующий вывод называется левым выводом цепочки из ₀ в грамматике G. Правый вывод определяется аналогично.

Если S= = w – левый вывод терминальной цепочки w, то каждая цепочка (0i<n) имеет вид , где ^, N и (N)^.

Каждая следующая цепочка левого вывода получается из предыдущей цепочки заменой самого левого нетерминала правой частью некоторого правила.

Пример. Рассмотрим КС-грамматику G₀ с правилами

EE+T | T

TТ*F | F

F(Е) | a.

Нарисуем дерево вывода (рис 3.7).

Рис. 3.9. Пример дерева вывода

Это дерево служит представлением десяти эквивалентных выводов цепочки а+а.

Е Е+Т Т+Т F+Т а+Т а+Fа+а – левый вывод.

Е Е+Т Е+F Е+а  Т+а F+аа+а – правый вывод.

Определение. Цепочку  будем называть левовыводимой, если существует левый вывод S= = , и писать S. Аналогично  будем называть правовыводимой, если существует правый вывод S= = , и писать S. Один шаг левого вывода будем обозначать , а правого