64 Пути в бесконтурном графе. Общая теория:
У нас есть граф G=(V,E), где связь между вершинами v и w следующая: a(v,w) 
E. Если связь между вершинами отсутствует, то a(v,w)=
.
Если последняя вершина wo, w1, …, wn определяет путь в графе, то его длина равна суммарному весу входящих вершин:
Наша задача – нахождение кратчайшего пути между вершинами S, t. M(S,t) – расстояние между S и t. Путь из S в t, который имеет минимальную длину – есть кратчайший путь, между вершинами S и t. d(S,t)=d(S,vk) + a(vk,t)
d(S,vk)=d(S,vk-1)+a(vk-1,vk)
vk-1 |
vk |
t
S
Поиск кратчайшего пути в бесконтурном графе:
Поиск кратчайшего пути в бесконтурном графе имеет 2 части. Первая переименование вершин графа так, что первая вершина не имеет входящих вершин. Вторая часть сам поиск кратчайших путей.
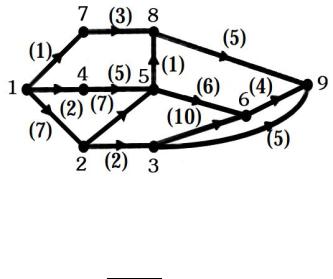
Для начала зададим произвольный бесконтурный граф с произвольной нумерацией и весами.
И запишем его в виде матрице смежности, где ребра которые не входят в другие ребра будем отмечать максимально большим числом 32767.
Для перенумерации графа, так чтобы вершина №1 имела только исходящие ребра, используем алгоритм Topolsoft.
Алгоритм Topolsoft (G,N)
1)for each v ϵ V do p[v] 
0
2)for each w ϵ V do
3)for each v ϵ V
4)p[v] 
p[v]+1
5)end for
6)end for
7)Стек 
8)for each v ϵ V do
9)if p[v] = 0 then
10)Стек 
v
11)end if
12)end for
13)num 
0
14)while Стек ≠ 
do
15)w 
Стек
16)num 
num+1
17)N[w] 
num
18)for each v ϵ V
19)p[v] 
p[v]-1
20) |
if p[v] = 0 then Стек v |
21) |
end if |
22)end for
23)end while
24)end for
После чего получим следующую нумерацию графа.
Алгоритм поиска наикратчайших путей.
После можно найти кратчайшие расстояния от вершины №1 до каждой из вершин по алгоритму DSP.
Алгоритм DSP(G, N, d)
1)for j = 1 to n do d[vj] 
2)d[v1] 
0
3)for j = 2 to n do
4)for I = 1 to j-1 do
5)if d[vj] 
d[vi]+a[vi, vj] then
6)d[vj] 
d[vi]+a[vi, vj]
7)end if
8)end for
9)end for
10)end for
После выводим на экран результат. При этом вычислительная сложность считаем следующим образом:
И она составит: