
2. Вычислительная сложность алгоритма и ее оценка:
Требования к алгоритмам:
1.быть простым для понимания, перевода в программный код и отладки;
2.эффективно использовать вычислительные ресурсы и выполняться по возможности быстро. Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности задачи.
Классификация по эффективности:
1.О(1), то его вычислительная сложность не зависит от количества элементов в структуре.( поиск минимального или максимального значения в упорядоченном );
2.О(n) - линейный. (присоединение элемента к концу очереди )
3.О(log2 n) -логарифмический. (алгоритмы обработки бинарного дерева)
4.О(n2) - квадратический (алгоритмы сортировки вставками, обменной сортировки).
5.О(n3) - кубический. (алгоритм Уоршалла на графе).
6.О(2n) - экспоненциальный.
Порядок роста функции:
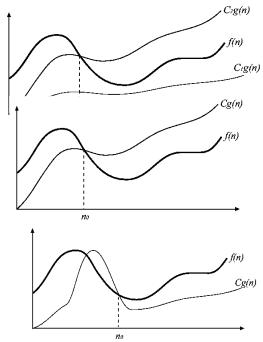
Порядок роста f(n)=O(g(n)), если существуют такие числа
, >0 и целое , что |
g(n)≤f(n)≤ g(n) для всех n≥ |
, f(n) |
и g(n)→+∞. f(n)=O(g(n)): |
|
|
Оценка сверху: |
|
|
f(n)=O(g(n)), если существуют такое число с>0 и целое |
, что |
|
f(n)≤c g(n) для всех n≥ |
, f(n)=O(g(n)): |
|
Оценка снизу:
f(n)=ω(g(n)), если существуют такое число с>0 и целое , что f(n)≤c g(n) для всех n≥ , f(n)= ω(g(n)):
