Разработка регистра признаков результата.

Регистр признаков хранит информацию о результате работы устройства. Регистр состоит из 4 триггеров. Первый дает единицу, если результат отрицательный, второй — если положительный, третий — если равен нулю, четвертый — если произошло переполнение (при этом первые три триггера блокируются). Входными сигналами для первых двух триггеров является знак результата. Для триггера равенства результата нулю необходимый входной сигнал получается на комбинационной схеме, которая вырабатывает сигнал единицы, когда все значащие разряды (двоичные) результата равны нулю. Входным сигналом четвертого триггера является сигнал с выхода схемы переполнения.

Для блокировки первых трех триггеров в случае переполнения на входы Jэтих триггеров следует также подать инверсию сигнала со схемы, фиксирующей переполнение. На все четыре триггера на синхровходыCподается сигнал СИ3 от распределителя сигналов. На инверсные входыRподается сигнал НУ для перевода триггеров в начале выполнения операции в нулевое состояние.

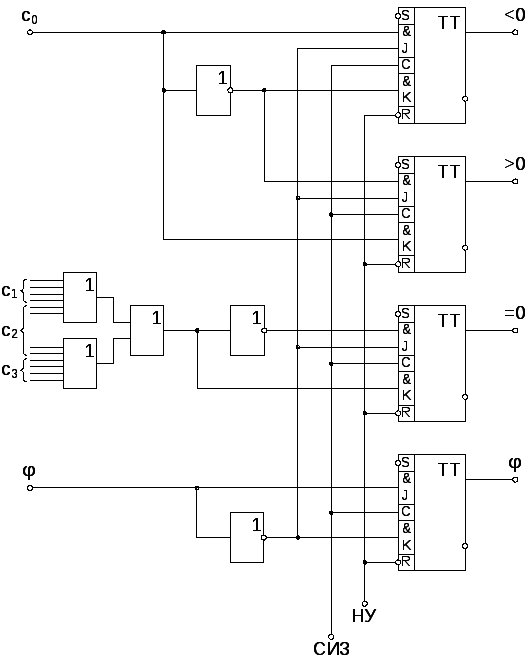
Расчет временных параметров устройства управления.

Устройство, вырабатывающее управляющие сигналы СИ1, СИ1, СИ3 и СИ4, называется распределителем сигналов.

Распределитель сигналов имеет 4 выхода и предназначен для управления процессом работы устройства. Назначение сигналов, на каждом из четырех выходов распределителя:

первая ветка: сигнал подается на синхровход Cрегистров входов, происходит занесение данных в регистры;
вторая ветка: сигнал подается на синхровход Cрегистров выходов, происходит занесение данных в регистры;
третья ветка: сигнал подается на синхровход Cрегистра признаков, происходит занесение флагов окончания процесса в регистр;
четвертая ветка: сигнал подается на асинхронный вход Rтриггера пуска, происходит останов процесса.

Входными сигналами распределителя сигналов являются импульсы с генератора импульсов. Генератор вырабатывает импульсные сигналы длительностью 2 нсек со скважностью 1. Распределитель сигналов должен «выделить» из этой последовательности 4 сигнала с определенной временной задержкой между ними.

При проектировании подобного распределителя сигналов, в первую очередь необходимо определить временные интервалы Т₁, Т₂иT₃.

Т₁— характеризуется временем работы трехразрядного десятичного сумматора комбинационного типа. Для определения этой величины надо определить время задержки сигналов по каждой схеме, которая входит составной частью в общую схему.

Начнем с одноразрядного двоичного сумматора. Задержка по цепи вход-выход Р будет определяться тремя ЛЭ и равна 3 нсек. Задержка вход-выход S (по самой длинной цепи) будет определяться пятью ЛЭ и равна 5 нсек.

Расчет задержки сигналов в одноразрядном десятичном сумматоре. При определении этих значений необходимо исходить из общей картины работы сумматора. Будем анализировать самые «длинные цепи». Два слагаемых приходят на входы устройства, и есть перенос по всем 4 разрядам. Сигнал γ’₈появится с задержкой 11 нсек (2 нсекx4 разр.). Далее сигнал проходит цепь коррекции и в точке F_кбудет с задержкой 14 нсек (11 нсек + 3 нсек). Следовательно, по выходу П_iзадержка будет 15 нсек. Далее сигнал идет через двоичные сумматоры ввода коррекции, и на выходеγ₈появится через 26 нсек (15 нсек + 3 нсек + 3 нсек + 5 нсек).

Задержка в преобразователе будет 3 нсек (1 нсек x3 ЛЭ).

Расчет задержки сигналов в трехразрядном десятичном сумматоре также необходимо проводить, используя знания принципов сложения величин. При поступлении двух слагаемых на входы самой длинной цепью будет: прохождение операндов через преобразователи и поступление на сумматоры: со входов DC3 сигнал по П_iпойдет на вход П_i_-1DC2; со входа П_i_-1DC2 через выход П_iDC2 на вход П_i_-1DC1; со входа П_i_-1DC1 через П_iDC1 на вход учитывающего знак суммы сумматораSM; со входа сумматора через выходPна вход П_i_-1DC3; со входа П_i_-1DC3 на выходы этого сумматора и через выходной преобразователь на выходы устройства. Итого: 77 нсек (3 нсек + 14 нсек + 14 нсек + 14 нсек + 3 нсек + 26 нсек + 3 нсек).

Так как Т₁должно быть кратно 4 (длительность импульса 2 нсек и промежуток между импульсами также 2 нсек) и более 77 нсек, то Т₁= 80 нсек.

Временной интервал Т₂определяется задержкой сигнала во входных цепях регистра признаков. Комбинационная схема на входе триггера, отвечающего за признак равенства нулю результата, имеет задержку 3 нсек, поэтому Т₂= 4 нсек.

Величина Т₃также равна 4 нсек, так как сигнал останова СИ4 идет непосредственно за сигналом СИ3.

Имея временные интервалы между выходными сигналами в распределителе сигналов, можно приступить к проектированию данного устройства. Распределитель сигналов является генератором следующих четырехразрядных двоичных чисел:

0001,	0000, … , 0000	, 0010, 0100, 1000

	19 раз

Распределитель сигналов будет проектироваться на основе счётчика с пересчётом на 23 и комбинационной схемой на выходе. Для проектирования счётчика понадобиться 5 триггеров.

Составим таблицу переходов.

Таблица переходов

Такт n					Такт n+1					Функции переходов					Синхроимпульсы
Q₅ⁿ	Q₄ⁿ	Q₃ⁿ	Q₂ⁿ	Q₁ⁿ	Q₅ⁿ⁺¹	Q₄ⁿ⁺¹	Q₃ⁿ⁺¹	Q₂ⁿ⁺¹	Q₁ⁿ⁺¹	F₅	F₄	F₃	F₂	F₁	СИ4	СИ3	СИ2	СИ1
0	0	0	0	0	0	0	0	0	1	0	0	0	0	▲	0	0	0	1
0	0	0	0	1	0	0	0	1	0	0	0	0	▲	▼	0	0	0	0
0	0	0	1	0	0	0	0	1	1	0	0	0	1	▲	0	0	0	0
0	0	0	1	1	0	0	1	0	0	0	0	▲	▼	▼	0	0	0	0
0	0	1	0	0	0	0	1	0	1	0	0	1	0	▲	0	0	0	0
0	0	1	0	1	0	0	1	1	0	0	0	1	▲	▼	0	0	0	0
0	0	1	1	0	0	0	1	1	1	0	0	1	1	▲	0	0	0	0
0	0	1	1	1	0	1	0	0	0	0	▲	▼	▼	▼	0	0	0	0
0	1	0	0	0	0	1	0	0	1	0	1	0	0	▲	0	0	0	0
0	1	0	0	1	0	1	0	1	0	0	1	0	▲	▼	0	0	0	0
0	1	0	1	0	0	1	0	1	1	0	1	0	1	▲	0	0	0	0
0	1	0	1	1	0	1	1	0	0	0	1	▲	▼	▼	0	0	0	0
0	1	1	0	0	0	1	1	0	1	0	1	1	0	▲	0	0	0	0
0	1	1	0	1	0	1	1	1	0	0	1	1	▲	▼	0	0	0	0
0	1	1	1	0	0	1	1	1	1	0	1	1	1	▲	0	0	0	0
0	1	1	1	1	1	0	0	0	0	▲	▼	▼	▼	▼	0	0	0	0
1	0	0	0	0	1	0	0	0	1	1	0	0	0	▲	0	0	0	0
1	0	0	0	1	1	0	0	1	0	1	0	0	▲	▼	0	0	0	0
1	0	0	1	0	1	0	0	1	1	1	0	0	1	▲	0	0	0	0
1	0	0	1	1	1	0	1	0	0	1	0	▲	▼	▼	0	0	0	0
1	0	1	0	0	1	0	1	0	1	1	0	1	0	▲	0	0	1	0
1	0	1	0	1	1	0	1	1	0	1	0	1	▲	▼	0	1	0	0
1	0	1	1	0	0	0	0	0	0	▼	0	▼	▼	0	1	0	0	0