Пример 2.3. Функционирование производства в случае оу

Рассматривается принцип открытого управления. Имеется 40 предприятий со следующими характеристиками:

Необходимо найти:

оценки эффективности, сообщаемые предприятиями центру;

цену продукции и планы предприятий, назначаемые центром.

В нашем случае присутствует явный монополист — первое предприятие. При большом количестве предприятий с малой эффективностью, все они будут сообщать примерно реальные коэффициенты эффективности: .

Для предприятия-монополиста можно воспользоваться приближенной формулой определения сообщаемой оценки: .

Тогда цена на продукцию будет

Планы, которые получат предприятия:

Недостатком закона ОУ является искажение сообщаемой предприятиями информации о коэффициентах эффективности. Это искажение тем более значительно, чем больше разница между сообщаемыми оценками и реальными коэффициентами эффективности

Попытаемся устранить указанный недостаток введением дополнительных механизмов воздействия на предприятие.

Рассмотрим следующие виды открытого управления:

• дифференцированные цены;

• штрафы;

• адаптивный способ формирования данных;

• нормирование целевых функций.

Дифференцированные цены

Введем индивидуальные цены для каждого предприятия:

. (2.6)

Центр не может определить на этапе планирования, поскольку цена зависит от реальной эффективности , с которой работает -е предприятие. Центр вычисляет норматив (из сообщаемых оценок эффективности предприятий) и сообщает предприятию i. Цену предприятие определяет самостоятельно на этапе реализации по формуле (2.6). Подставляя закон планирования и закон ценообразования (2.6) в целевую функцию предприятия, получим

. (2.7)

Заметим, что из следует, что Эти ограничения означают, что предприятие не может работать с эффективностью, превышающей .

Дифференцируя по , получаем уравнение для равновесной стратегии

.

Его единственное решение (т. е. единственной разумной стратегией поведения для любого предприятия является работа с такой же эффективностью, о которой предприятие сообщает центру). Подставляя решение в формулу (2.7), получаем

. (2.8)

Определим теперь оптимальные затраты i-го предприятия или реальный коэффициент эффективности производства: . Дифференцируя (2.8) по , получаем

.

Приравнивая производную нулю, получаем или, учитывая, что можно записать: Отсюда следует, что если для любого предприятия, то применение дифференцированных цен дает , т. е. план в ситуации равновесия совпадает с оптимальным.

Однако, если для i-го предприятия то , и план в ситуации равновесия не является оптимальным. Тем не менее эффективность закона управления и в этом случае повышается. Так, при план в ситуации равновесия является оптимальным. В то же время для закона ОУ при имеем . И только в случае монополиста применение дифференциальных цен практически не дает эффекта по сравнению с законом ОУ. При любая ситуация , где является ситуацией равновесия.

Штрафы

Пусть центр планирует не только количество выпускаемой продукции, но и затраты на производство (либо другое: себестоимость, прибыль и т. д.). Обозначим через планируемую величину затрат, которая определяется на основе , а именно: .

При любом отклонении реальных затрат от планируемых предприятие штрафуется. Пусть функция штрафа:

где — коэффициенты штрафа за занижение и завышение оценок затрат по сравнению с реальными .

В этом случае целевая функция предприятия примет вид

.

Поскольку в системе без штрафов , а значит , то достаточно провести анализ ситуации В этом случае целевая функция предприятия будет выглядеть следующим образом:

.

Рассмотрим два случая штрафов:

1) случай слабых штрафов — . Здесь прибыль — убывающая функция . Подставим в целевую функцию:

.

Дифференцируя функцию по и учитывая, что , получаем

(2.9)

где

2) случай сильных штрафов — : прибыль — возрастающая функция В такой ситуации единственное разумное поведение предприятий — максимизировать реальные затраты и установить их равными плановым затратам: (так как Тогда сообщаемые оценки будут равны реальным коэффиицентам эффективности предприятий: .

Пусть , тогда , в этом случае мы получаем следующую ситуацию равновесия:

Ситуация равновесия для случая сильных штрафов совпадает с ситуацией равновесия для случая дифференцирования цен. Эффективность закона ОУ также совпадает. Так, например, при наличии в системе монополиста применение даже сильных штрафов практически не дает эффекта.

Заметим, что даже в случае слабых штрафов может сложиться ситуация, когда все предприятия будут сообщать свои реальные оценки эффективности. Минимальное , при котором , определяется из условия .

Пример 2.4. Открытое управление в случае слабых штрафов

Дано:

Действует принцип открытого управления, причем центр ввел штрафы на отклонение от планируемых затрат:

Минимально возможное (из ), тогда

следовательно,

Для остальных предприятий расчет сообщаемых оценок эффективности проводится итерационным методом по формуле (2.9). Рассчитывая для остальных предприятий, получаем:

Адаптивный способ формирования данных

При адаптивном способе формирования данных оценка определяется центром не путем опроса предприятий, а на основе известных планов, затрат и оценок в предыдущие периоды функционирования. Примем, что , где — план и затраты в периоде ; — оценка коэффициента эффективности производства в периоде k.

В этом случае выбор предприятием конкретной величины затрат в данном периоде функционирования повлияет на план и цену продукции в будущем. Одним из свойств активности ор-ганизаций является учет последствий принимаемых «сегодня» решений. Для формализации этого свойства примем, что интересы предприятия в рассматриваемом периоде (нулевом) определяются стремлением к максимуму взвешенной суммы при-былей в данном и будущих периодах:

(2.10)

где — дисконтирующий множитель ( будущие прибыли учитываются с меньшим весом).

Выражение (2.10) будем называть критерием эффективности с учетом будущих периодов. Выбор , по существу, эквивалентен выбору достигнутого коэффициента эффективности , который и принимается за оценку следующего периода. Выбор мы будем считать стратегией i-го предприятия в рассматриваемом периоде . Для упрощения примем следующую гипотезу поведения: предприятие предполагает, что достигнутая эффективность остается неизменной в будущие периоды, следовательно, и оценка будет равна для любого . Тогда критерий эффективности примет вид:

(2.11)

где — степень дальновидности предприятия.

Подставляя закон ОУ (2.2) в выражение (2.11) и учитывая, что получаем следующий вид критерия эффективности:

(2.12)

Ситуацию равновесия будем называть устойчивой по пе-риодам функционирования, если . Для ее оп-ределения дифференцируем критерий эффективности (2.12) по

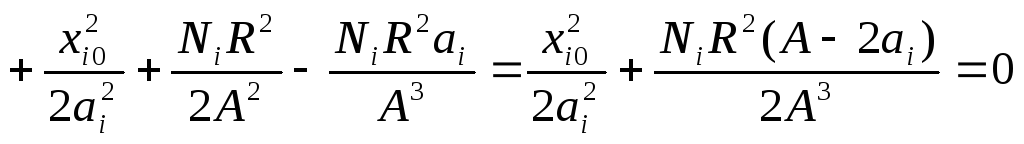. (2.13)

Подставляя в (2.13), получаем

или

Окончательное уравнение для ситуации равновесия примет следующий вид:

Результаты анализа во многом аналогичны случаю сильных штрафов: при имеем и

93