эффективности Если то а если то обязательно . Пусть предприятия упорядочены по возрастанию .

Рассмотрим пять возможных случаев соотношения спроса и предложения:

1. (предложения на выпуск продукции со стороны предприятий существенно превышают спрос R). Здесь единственная ситуация равновесия . При этом

2. (предложения на выпуск продукции со стороны предприятий превышают спрос). Определим минимальное такое, что (т. е. для оставшихся предприятий 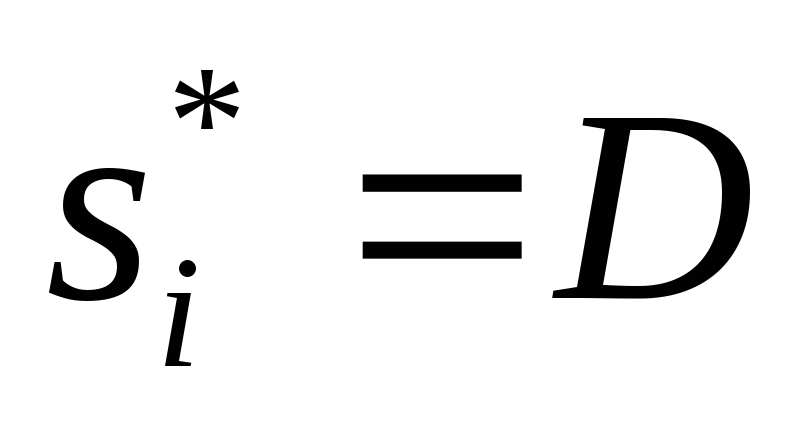аналогично первому случаю). Тогда равновесная ситуация будет определяться следующим образом:

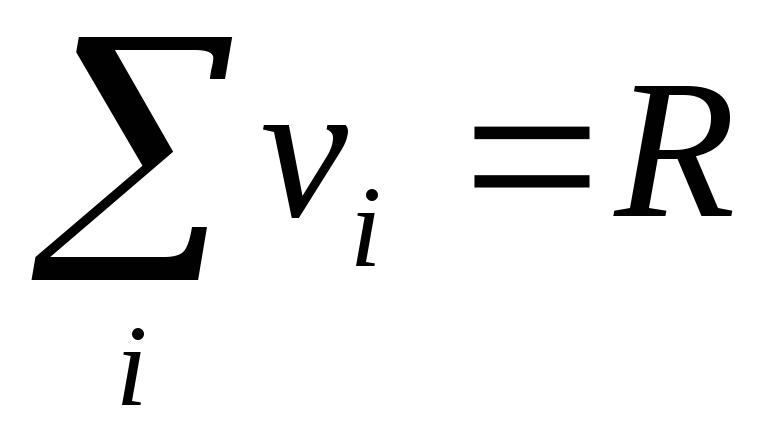3. (баланс спроса и предложения). Здесь равновесна любая ситуация , так как . Из условия 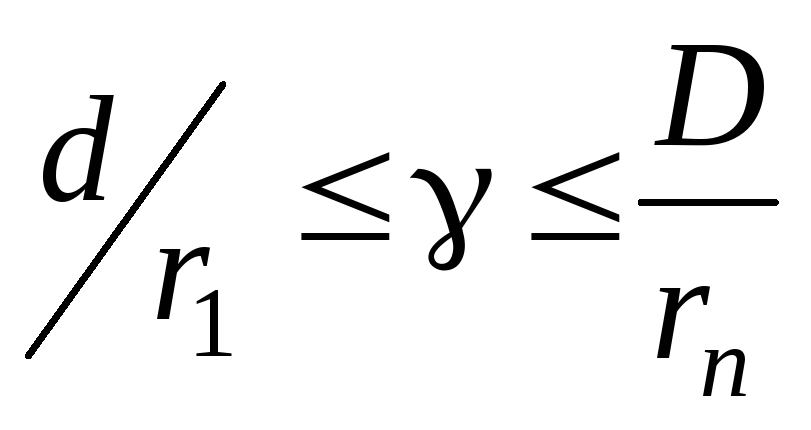( не может быть больше D и не может быть меньше d). В этом случае можно взять просто ;

4. (спрос на продукцию превышает предложения со стороны предприятий). Определим максимальное k такое, что . В данном случае единственная ситуация равновесия будет вычисляться по формуле

5. (спрос на продукцию существенно превышает предложение со стороны предприятий). Единственная ситуация равновесия:

Пример 2.1. Функционирование производства в условиях жу

Пусть у нас имеется пять предприятий, работает принцип ЖУ,

Необходимо определить планы предприятий, затраты центра при ЖЦ и прибыли предприятий.

Предприятия «желали» бы выпускать продукцию в следующих объемах:Для заданных условий определим, какой из вышеперечисленных вариантов действует в нашем случае. Здесь т. е. предложение превышает спрос. Определим

Тогда равновесная ситуация:

Оценки эффективности, сообщаемые предприятиями центру:

Тогда планы предприятий примут значения:

Затраты центра составят:

Прибыли предприятий:

Заметим, что для случаев 1 и 5 план в ситуации равновесия совпадает с полученным при использовании только имеющейся информации о границах . Эти случаи являются самыми неблагоприятными режимами работы системы с точки зрения ее эффективности. Поэтому эффективность законов ЖЦ для этих случаев в точности равна : дополнительная информация не дает эффекта.

Эффективность рассмотренного закона ЖЦ можно повысить, если ввести штрафы за искажение информации. Пусть на этапе реализации центр может оценить реальные затраты на выпуск продукции и тем самым реально достигнутое значение эффективности . Это позволяет ввести в целевую функцию составляющую, соответствующую штрафу при отклонении от сообщенной оценки Рассмотрим случай «сильных штрафов», когда единственной разумной стратегией предприятия является совпадение реальной и планируемой эффективности. Так как , то сообщаемая оценка в случае сильных штрафов также должна удовлетворять условию . При этом , и целевая функция (2.1) примет вид

.

Покажем, что если , то — единственная ситуация равновесия: при оба сомножителя и являются возрастающими функциями , следовательно — возрастающая функция . Поэтому максимальное значение достигается на границе . Таким образом, установив достаточно высокую цену продукции, центр может обеспечить оптимальное функционирование системы (в смысле минимизации затрат на производство продукции), тогда коэффициент эффективности управления будет равен 1. Для этого достаточно взять . Однако цена продукции при малых значениях d может быть значительно больше, чем оптимальная цена . Если же взять , то возможен случай , игровой анализ которого является более сложным: достоверность оценок и оптимальность планов удается обеспечить только при достаточно высокой . Рассмотрим ситуацию с заниженной ценой на примере

Пример 2.2. Жесткая централизация для случая сильных

штрафов и низкой ценой

Действуют принцип ЖЦ и «сильные штрафы».

Имеем . Если все предприятия сообщают достоверные оценки, то . В этих условиях каждому предприятию выгодно сообщать минимальную оценку (при условии, что все остальные сообщают достоверные оценки), т. е. ситуация не является точкой Нэша. Проанализируем ситуации, в которых k предприятий сообщают достоверные оценки, а остальные — минимальную оценку:

а) случай, при котором уже рассмотрен;

б) . Прибыль (потери) для предприятия, сообщившего минимальную равна , для остальных — ;

в) Потери предприятий с минимальной оценкой увеличатся и составят теперь , для осталь-ных —

г) . Потери предприятий, сообщивших минимальные оценки, равны –22 , для предприятий, сообщивших достоверные оценки: –110;

д) . Потери предприятий, сообщивших минимальные оценки, равны –50 , для предприятий, сообщивших достоверные оценки, равны –250;

е) . Прибыль всех предприятий равна –180.

Здесь ситуация (е) является единственной равновесной ситуацией, но не «разумной». Действительно, существуют ситуации (а), (б) и (в) более предпочтительные для всех предприятий. Тем не менее для осуществления этих ситуаций часть предприятий, а именно ситуации (б) и (в), либо все предприятия, т. е. ситуация (а), должны договариваться. При этом всегда существует соблазн обмануть «товарищей по договору» и получить меньшие потери. Таким образом, при низких ценах выбор наилучшей ситуации с точки зрения всех участников (предприятий) остается весьма противоречивой задачей.