ЭМ лекции / Модел-2-пр3

Например, роль центра могут играть потребители, которые в первую очередь будут брать продукцию, предлагаемую по минимальной цене. Упорядочим предприятия по возрастанию цены: . Пусть предприятие k такое, что

Тогда последние (n – k) предприятий вынуждены снижать цену, а первые () будут повышать цены (их прибыль будет расти). Следовательно, в равновесии установится единая рыночная цена продукции, т. е. . Пусть — выпуск i-го предприя-тия при цене (очевидно, ). Если , то, установив цену (— малое положительное число), предприя-тие i сможет реализовать продукцию в количестве и получить дополнительную прибыль. Поэтому в равновесии и из условия находим

.

Заметим, что ситуация не является равновесием Нэша, поскольку любое предприятие может, установив цену при сохранении выпуска , увеличить свою прибыль. Однако при этом остальные предприятия могут увеличить выпуск продукции, установив цены , что может привести к тому, что продукция предприятия i не найдет сбыта. Поэтому при достаточно большом числе предприятий повышение цены сверх нецелесообразно. В этом смысле ситуация является равновесной. Таким образом, в равновесии выпуски продукции являются оптимальными.

Учтем влияние отдельной фирмы на рыночную цену. Пусть фирма i установила цену . Тогда остальные фирмы, устанавливая цены ( — малое положительное число), смогут реализовать продукцию в количествах , а фирма i только продукцию в объеме , получая прибыль .

Определяя максимум прибыли по , возьмем производную от целевой функции предприятия и приравняем ее нулю:

Отсюда получаем оптимальную цену для предприятия:

Заметим, что полученная цена больше оптимальной что видно из следующих преобразований:

В случае наличия фирмы-монополиста устанавливается монопольная цена (эта ситуация совпадает с наличием монополиста при принципе ОУ).

Но до сих пор мы не учли, что спрос на продукцию падает при увеличении цены . Пусть, например, спрос — линейная функция цены , где , что обеспе-чивает при . Найдем цену из условия максимума:

отсюда .

Пусть коэффициенты эффективности всех предприятий рав-ны между собой: . Тогда

.

График зависимости от n приведен на рис. 2.2.

Цену в случае одного предприятия назовем монопольной ценой

Пример 2.6. Функционирование предприятий

в условиях рыночной системы

В условиях рыночной системы действуют пять предприятий со следующими коэффициентами эффективности: Пусть Определить объемы выпусков и прибыли предприятий:

1) в ситуации равновесия;

2) если 5-е предприятие установит собственную цену на продукцию:

а) при независимости спроса от цены;

б) если спрос падает при увеличении цены и

1. и

Прибыли предприятий:

2. Для случая а: цена, установленная пятым предприятием:

.

Для случая б:

тогда

При данных условиях пятому предприятию выгодно устанавливать свою цену, даже если при этом падает спрос на продукцию.

2.2.3. Полная децентрализация планирования

При децентрализованном планировании предприятия не могут самостоятельно устанавливать цену продукции, но могут выпускать ее в любом количестве. Для простоты примем, что центр принимает от предприятий всю произведенную продукцию, однако при отклонении общего количества от R в системе возникают потери, с учетом которых целевая функция центра принимает вид

,

где — достаточно большое число.

Как правило, цена в системах с полной децентрализацией планирования определяется на основе адаптивного способа формирования данных. Простейшим является «управление по отклонению». Если в периоде k суммарный выпуск продукции меньше спроса , то цена в следующем периоде увеличивается, а если суммарный выпуск продукции превышает спрос , то цена уменьшается. Пусть, например, цена в -ом периоде определяется по формуле

(2.21)

где — дефицит продукции в периоде k (отрицательный дефицит означает избыток продукции).

Равновесие при гипотезе СВ определяется соотношениями:

или .

Пусть — цена в периоде . Исследуем вопрос о схо-димости последовательности цен к равновесию , считая, что в периоде k предприятие i выпускает продукцию в количестве В этом случае формула (2.21) примет вид

Выразив через получаем:

Заметим, что если выполняется ограничение , то . Таким образом, последовательность сходится к оптимальному выпуску , а последовательность цен — к цене . Следовательно, чтобы гарантировать сходимость, достаточно установить .

Ситуация немного сложнее, если не учитывать гипотезу СВ, т. е. если влияет на цену . В этом случае целевая функция предприятия выглядит следующим образом:

(2.22)

где .

Необходимо однозначно определить .

Пусть предприятие принимает цену за равновесную и в соответствии с этим определяет равновесный выпуск (простейшая гипотеза). Будем считать пару равновесием, если и последовательность обеспечивает максимум целевой функции (2.22) на множестве всех последовательностей вида . Для таких последовательностей целевая функция (2.22) примет вид:

где — степень дальновидности предприятия;

.

Дифференцируя по получаем

так как — выпуск в ситуации равновесия, то и получаем

.

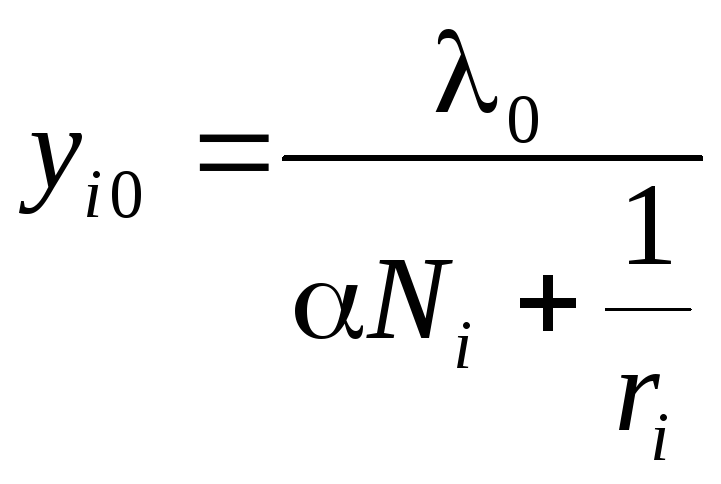Таким образом, выпуск однозначно определяется ценой в данном периоде. Рассмотрим последовательность

. (2.23)

Подставляя (2.23) в формулу (2.21), получаем:

Обозначим , тогда .

Если то для , следовательно, .

Так как — убывающая функция и возрастающая функция , то : достаточное условие сходимости совпадает с условием сходимости при гипотезе СВ.

Проанализируем ситуацию равновесия:

1. цена в ситуации равновесия превышает оптимальную цену: так как хотя бы для одного предприятия;

2. выпуски могут быть далеки от оптимальных. Например, если все предприятия являются «очень дальновидными»: и вообще не зависят от 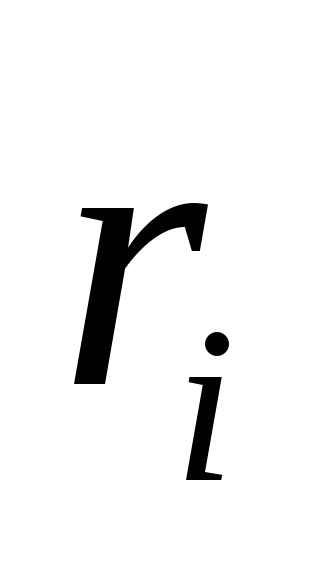. Более того, ес-ли (более эффективное предприятие является и более даль-новидным), то — объем выпускаемой продукции обратно пропорционален , а не прямо пропорционален, как при

3. если P — некоторое множество предприятий «очень дальновидных» , а остальные предприятия — недальновидные то

.

Если .

Парадокс дальновидности. Пусть (n — «очень дальновидное» предприя-тие). Тогда .

Таким образом, дальновидное предприятие фактически не выпускает продукцию и его прибыль равна нулю, а недальновидные получают вполне реальную прибыль в каждом периоде функционирования. Этот парадокс показывает, что «отказывать себе сегодня во всем» столь же неразумно, как и «жить только сегодняшним днем».

Можно предложить и другие способы установления цены. Пусть, например, центр предполагает, что предприятия действуют в периоде k, исходя из гипотезы СВ. Тогда , и центр может определить оценки эффективности предприятий на следующий период по формуле

Тогда цена продукции в следующем периоде будет определяться как

. (2.24)

Закон ценообразования (2.24) интересен тем, что если предприятия действительно придерживаются гипотезы СВ, то сходимость в ситуацию равновесия обеспечивается за один период независимо от начальной цены . Проведем анализ ситуации равновесия. Считаем, что предприятия выбирают величину , предполагая цену равновесной. Получаем

Дифференцируя по , получаем

.

Из условия получаем

.

Тогда цена определяется выражением

.

Сходимость обеспечивается, если . При (все предприятия одинаковы), имеем

.

Равновесная цена:

Вопросы для самопроверки

1. Какой информацией обладает центр в модели управления производством продукции?

2. Сформулируйте задачу центра.

3. Перечислите различные способы организации взаимоотношений между центром и предприятиями.

4. В чем заключается принцип жесткой централизации?

5. В чем заключается принцип открытого управления?

6. Сформулируйте гипотезу слабого влияния.

7. Как зависит эффективность открытого управления от количества предприятий?

8. Какими показателями характеризуется степень централизации управления?

9. Что такое «рыночная система»?

110