Пример 4.9. Распределение затрат на объект

Соседними муниципалитетами ведется строительство совместной системы водоснабжения. Пусть у нас есть три города, которые при строительстве могут понести следующие затраты:

город отдельно — 120; город— 140; город— 120;

коалиция — 170; коалиция— 190; коалиция— 160; три города вместе — 265.

Здесь х.ф. игры задана в виде затрат, а не прибыли. Будем обозначать х.ф. по затратам В данном примерепредставляет собой минимальные затраты на обслуживаниеSнаиболее эффективным способом.

Рассмотрим сначала объединение двух городов иЭкономия затрат от совместного производства составит

Равное распределение этой экономии (эгалитарное решение) при-водит к следующим затратам:

Если участвуют все три города, общая экономия составит

Распределим экономию равным образом между игроками:

Приемлемость такого распределения затрат проблематична. Общие затраты, получающиеся для коалиции , превосходят их затраты без города:а значит такое распределение не устроит коалицию

Таким образом, дележ не принадлежит с-ядру.А существует ли в этой игре с-ядро? Для существования ядра необходимо, чтобы выполнялись следующие условия:

При этих ограничениях игра не имеет решения (хотя свойство супераддитивности выполняется). Следовательно, необходимо усилить свойство супераддитивности.

Примечание. Если в игре указаны не прибыли игроков, а их затраты, то при проверке условий меняются знаки сравнения. Так, принадлежность дележа с-ядру в этом случае будет определяться неравенством

Будем называть коалицию собственной, если она не совпадает с максимальной коалицией .

Определение. Для данного сообщества игроков сбалансированное покрытие есть такое отображение из(множества собственных коалиций) в множество действительных чисел на интервале [0, 1], чтодля всех игроков , где суммирование ведется по всем собственным коалициям, содержащим игрока .

Теорема. С-ядро игр с трансферабельными выигрышами не пусто тогда и только тогда, когда для любого сбалансированного покрытия выполняется условие

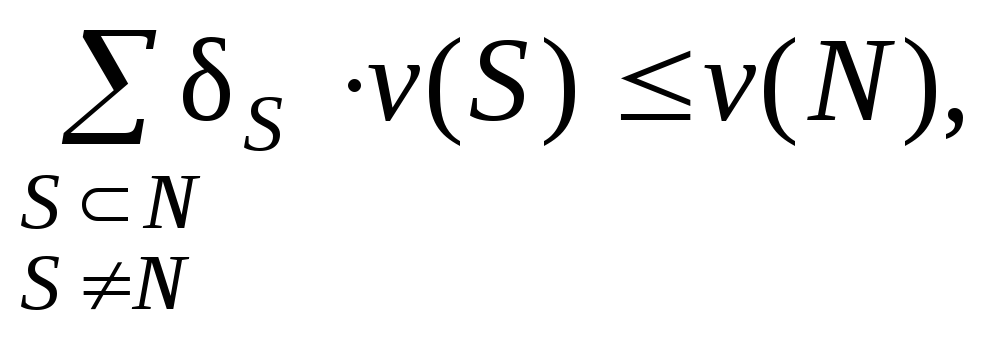(4.1)

если говорим о затратах то неравенство выглядит следующим образом:

Данное условие означает, что кооперативная прибыль собственных коалиций не должна быть слишком большой по сравнению с прибылью

Сбалансированные покрытия образуют выпуклый многогранник. Поэтому условие (4.1) достаточно проверить для крайних точек этого многогранника. Если найти данные точки, то свойство сбалансированности может быть записано как конечная система линейных неравенств на v.

Рассмотрим игры с тремя игроками: Здесь сбалансированные покрытия образуют многогранник с пятью крайними точками:

1)

2)

3)

4)

5)

1Если игра не имеет решения в чистых стратегиях, решение ищется аналогично в смешанных стратегиях. Решение антагонистических игр в смешанных стратегиях в данном пособии не рассматривается. При желании эти вопросы можно изучить самостоятельно (решение антагонистических игр рассматривается в любой книге, посвященной вопросам теории игр, например в [8]).

164