4.1.2. Эгалитаризм

Эгалитаризм основывается на принципе справедливости: к равноправным агентам должно быть равное отношение. Примене-ние этого принципа приводит к выравниванию индивидуальных полезностей. Интересным фактом является то, что принципы единогласия и равенства могут быть несовместными, при этом возникает известная дилемма равенство-эффективность.

Пример 4.1. Размещение объекта

А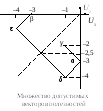дминистрацией двух городов, равных почисленности населения, выбирается место расположения совместного предприятия сферы обслу-живания (финансируемого извне). Городаисоединены двумя дорогами. Протяженность длинной дороги составляет 5 км, а короткой — 3 км.Обозначим черезточку, находящуюся на ко-роткой дороге на расстоянии 1 км от. Дорога на участке отдоBпроходит в горах, что не позволяет построить там данное предприятие. Таким образом,приходится выбирать место расположения предприятия либо на длинной дороге, либо между ина короткой дороге, что показано на рисунке.

Население каждого города заинтересовано в том, чтобы предприятие располагалось поближе к нему, поэтому полезность измеряется расстоянием до предприятия со знаком минус. Если расположить предприятие в пункте , то. На ри-сунке показано множество допустимых векторов полезностей.

Отрезок соответствует расположению предприятия на длинной дороге на расстоянии не более 1 км от городаотрезок— размещению на длинной дороге на расстоянии не менее 1 км от обоих городов. Отрезоксоответствует расположению предприятия на длинной дороге на расстоянии не более 1 км от городаОтрезоксоответствует расположению предприятия на короткой дороге междуи

Эффективным решением является размещение предприятия в городе или на короткой дороге между пунктамии(оптимальное по Парето решение всегда располагается на северо-восточной границе множества допустимых решений). Равенство полезностейдостигается только в одной точке — на середине длинной дороги. Получающийсявектор полезностейдоминируется по Паретовектором , соответствующим расположению предприятия в пункте.Возникает дилемма: мы можем выбрать размещение либо оптимальнымпо Парето, либо выравнивающим полезности, но не одновременно.

В примере в качестве решения выбирается размещение : оно является наиболее эгалитарным среди всех возможных эффективных размещений. С другой стороны, в точкеуровень полезностинаименее удачливого агента (т. е. уровень ) является наибольшимсреди всех возможных векторов полезностей:

для всех допустимых

Здесь два подхода выделили один и тот же исход однако, так бывает не всегда. Пусть множество достижимости содержит только два вектора:и. Оба являются эффективными, но векторминимизирует, а вектормаксимизирует. Если настаивать на симметричности агентов, то более предпочтительным следует признать вектор(из принципа анонимности, т. е. равенства агентов, следует, что векторыиравнозначны, однако последний доминируется по Парето вектором).

Максимизация коллективной функции полезности

на множестве достижимых векторов полезностей (максиминная процедура) состоит в выборе решения, которое бы максимизировало полезность наименее удачливого агента. Приняв уровень полезности наименее удачливого агента за индекс коллективной полезности, мы можем выполнить эгалитарную программу, не нарушив принципа анонимности. В дальнейшем функцию будем называть эгалитарной функцией коллективной полезности.

Корректная формулировка принципа эгалитарности не сводится к максимизации эгалитарной функции Функциясовпадает с уровнем полезности наименее удачливого агента. Если этот уровень достиг своего максимума, то можно к оставшимся агентам применить принцип эгалитарности.

Пример 4.2. Размещение объекта на кольцевой дороге

Пять городов соединенные кольцевой дорогой, выбирают место размещения совместного предприятия, что показано на рисунке.

Полезность снова измеряется расстоянием до предприятия со знаком минус. Предприятие можно расположить в любом месте на кольцевой дороге. Найдем наибольшие интервалы между парами городов и возьмем точки, диаметрально противоположные их серединам. Это и будут эгалитарные размещения. Таким образом, максиминная задача имеет два решения: в точкена расстоянии 1 км от городана дорогеи в точкена полпути между городамииСоответствующие вектора полезностей имеют вид:

Сравним решения ис позиции эгалитаризма. В обоих случаяхимеется два города с полезностью; следующий из наименееудачливых агентов в случае получает, а соответствующий агент в случаеполучает, поэтому при сравнении решений выбираемЗаметим, что не доминирует по Парето, но после упорядочения полезностейпо возрастанию получаем вектор который доминирует по Парето упорядоченный вектор полезностей

Лексиминное упорядочение коллективного благосостояния задает полный порядок на множестве допустимых векторов полезностей. Оно уточняет эгалитарную функцию коллективной полезности , когда имеется несколько допустимых векторов с одинаковым значением этой функции. Дадим строгое определение лексиминного порядка.

Определение. Пусть даны векторы Обозначим черезвекторы, упорядоченные по возрастанию. Векторыиявляются эквивалентнымив смысле лексиминного порядка, если выполнено равенство Будем говорить, чтовектор предпочти-тельнее вектора в смысле лексиминного порядка, если существует целое число для которого выполнены условия

В частности, если (т. е.), то векторлексикографически предпочтительнее.

Лексиминный порядок «работает» следующим образом: сначала сравниваются полезности «наиболее бедных» агентов в обоих распределениях, если же они совпадают, то сравниваются полезности «следующих по бедности» агентов и т. д.

Эгалитаризм достаточно сильно цементирует общество: когда все агенты делят поровну доход от кооперации, не может быть зависти или разочарования. Однако эгалитарный принцип перераспределения иногда трудно принять: увеличение на единицу полезности одного агента может привести к значительной потере суммарной полезности всех агентов. Рассмотрим распределение медицинской помощи между пациентами, застрахованными на равных условиях. Пусть объявлена цель обеспечения по возможности равного уровня здоровья пациентов. Это может означать, что мы должны постоянно отказываться от аспирина и антибиотиков для всех агентов, кроме одного, для того чтобы платить за дорогостоящее оборудование, которое продлит его жизнь хотя бы еще на один день. Вряд ли большинство людей согласится с подобным распределением.