Лекция 3

3. Типовые радиотехнические звенья

3.1 Основные виды звеньев

Устройства систем РА, имеющие различное конструктивное исполнение и принципы работы, могут описываться одинаковыми дробно-рациональными передаточными функциями – отношением полиномов с вещественными коэффициентами:

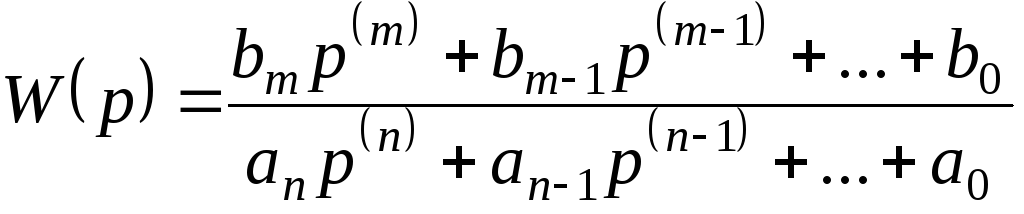
Такие полиномы имеют только действительные и комплексные попарно сопряженные корни. При разложении полиномов на множители каждый действительный корень дает линейный относительно оператора р двучлен, а каждая комплексно сопряженная пара – квадратный трехчлен с действительными коэффициентами. Каждый нулевой корень дает дополнительный множитель р. В результате передаточная функция приобретает следующий вид:

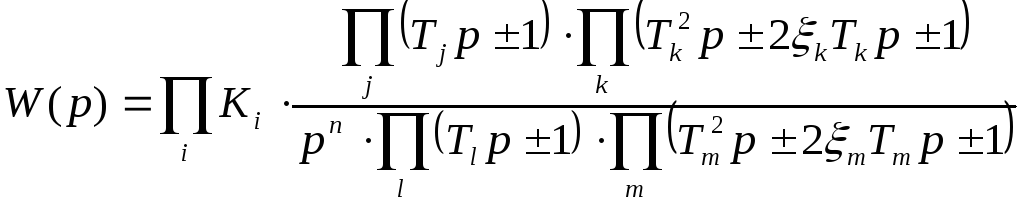
Каждый из сомножителей, классифицируемый своей передаточной функцией, называют типовыми радиотехническими звеньями.

Передаточная функция типового радиотехнического звена в общем виде представляется как произведение сомножителей следующего вида [3]:

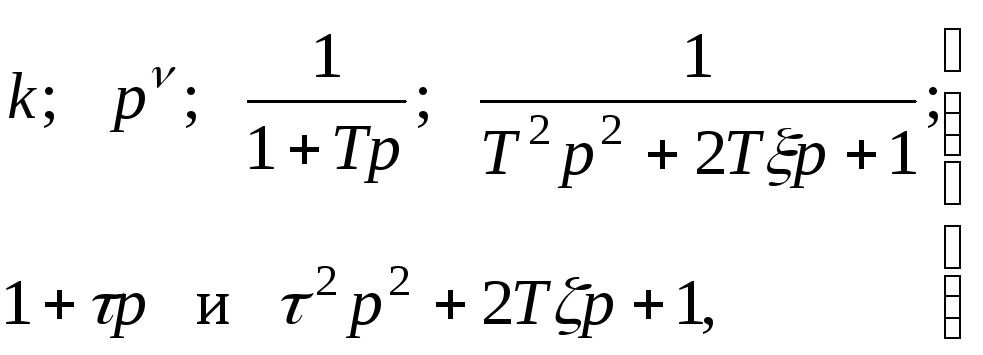(3.0)

где k, , T, , ,  – постоянные, причем k > 0, где  может быть положительным и отрицательным целым числом, T > 0, 0   < 1,  > 0, 0   < 1.

В соответствии с видом сомножителей (3.1) в табл. 3.1 приведены типовые радиотехнические звенья. В ней даны дифференциальные уравнения и передаточные функции этих звеньев, и показано их деление по основным свойствам.

Примечание: обозначения, принятые в таблице 3.1: k – коэффициент усиления; T,  – постоянные времени;  – коэффициент демпфирования (относительный коэффициент затухания); p – оператор Лапласа и дифференцирования.

В безынерционном звене при скачкообразном изменении входной величины мгновенно без какого-либо запаздывания изменяется и выходная величина – переходного процесса нет. В апериодическом звене выходная величина нарастает монотонно. Продолжительность переходного процесса зависит от второго параметра звена, называемого постоянной времени T. Чем больше постоянная времени, тем медленнее протекает переходной процесс.

Таблица 3.1  Типовые звенья радиоавтоматики

Название	Дифференц. уравнение	Передаточная функция
Идеальное усилительное (безынерционное)
Апериодическое (инерционное)
Апериодическое (инерционное) второго порядка	, где	, где
Колебательное	, где
Консервативное
Интегрирующее
Дифференцирующее
Форсирующее первого порядка

В апериодическом звене второго порядка переходной процесс также монотонный, но его продолжительность зависит от двух постоянных времени T₁, T₂.

Выходная величина колебательного звена в переходном процессе совершает колебания около того значения, которое должно установиться. Затухание колебаний зависит от значения третьего параметра звена, называемого коэффициентом демпфирования , который лежит в пределах от нуля до единицы. Чем больше , тем меньше отклонения и тем быстрее заканчивается переходной процесс.

Консервативное звено есть вырожденный случай колебательного звена (= 0). Возникшие в нем колебания не затухают. Передаточный коэффициент k указывает отношение амплитуды гармонических колебаний выходной величины к постоянной входной величине.

Интегрирующие звенья характеризуются тем, что при постоянном входном воздействии выходная величина неограниченно растет. У идеального интегрирующего звена передаточный коэффициент k определяет скорость этого роста. У реального интегрирующего звена такой режим устанавливается позднее и зависит от постоянной времени T.

Дифференцирующие звенья реагируют лишь на изменения входной величины. Например, если входная величина идеального дифференцирующего звена нарастает с постоянной скоростью, то выходная величина удерживается на постоянном уровне, пропорциональном этой скорости.

В природе идеальных дифференцирующих звеньев нет – они всегда имеют некоторую (хотя бы и очень малую) инерционность. При линейном нарастании входной величины реального дифференцирующего звена постоянное значение его выходной величины устанавливается не сразу, а тем позже, чем больше постоянная времени T.

Форсирующее звено сочетает в себе свойства безинерционного и дифференцирующего звеньев.