Авдот РА / Лекции РА 2013 / Лекция 7

5.3.4 Логарифмическая форма критерия Найквиста

Для проверки устойчивости замкнутой системы можно использовать логарифмические частотные характеристики разомкнутой, которые строятся почти без вычислений. Правила построения ЛАЧХ см. п.3.5. с. 33.

Формулировка критерия Найквиста. Для замкнутой системы необходимо и достаточно, чтобы на частотах, где ЛАЧХ положительна (т.е. (ω) > 0), фазовая частотная характеристика разомкнутой системы не пересекала ось  180⁰ или пересекала ее четное число раз.

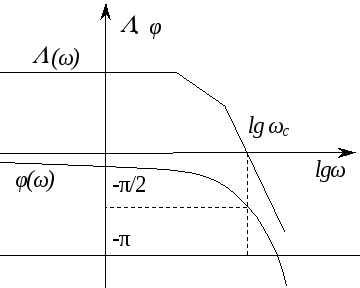
Рис. 5.1  Логарифмические частотные характеристики,

иллюстрирующие критерий Найквиста

Замкнутая система будет находиться на границе устойчивости, если на той же частоте, где (ω)=0, фазовая частотная характеристика разомкнутой системы пересекает ось – 180^о.

Вспомним основные положения по устойчивости систем:

1. По виду переходной характеристики. Переходные процессы в системе при t→∞ стремятся к определенной величине при любых начальных условиях.

2. По расположению нулей и полюсов ПФ системы. Чтобы система РА была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть.

3. По критерию Гурвица (алгебраический критерий для ПФ замкнутой системы высокого порядка) Для устойчивости линейной системы необходимо и достаточно, чтобы при значении коэффициентов a_n>0 все n определителей, получаемых из матрицы Гурвица Н, были положительны.

4. По критерию Михайлова (графоаналитический частотный, для исследовании замкнутых систем) Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении ω от 0 до ∞ начинался на вещественной оси в точке a₀ и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к ∞ в n-м квадранте.

5. критерий-Найквиста для разомкнутых систем

1