Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

633-izmer_dielictrich_mater

.pdf

Скачиваний:

Добавлен:

11.05.2015

Размер:

1.01 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧ и КР)

Измерение ε и tgδ диэлектрических материалов резонаторным методом

Руководство к лабораторной работе по дисциплине

«Микроволновая техника»

по направлению подготовки 210400.68 «Радиотехника»

2012

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)

Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧ и КР)

УТВЕРЖДАЮ Зав. кафедрой СВЧ и КР

_______С.Н. Шарангович

Измерение ε и tgδ диэлектрических материалов резонаторным методом

Руководство к лабораторной работе по дисциплине

«Микроволновая техника»

по направлению подготовки 210400.68 «Радиотехника»

Разработчики: профессор кафедры СВЧ и КР Гошин Г.Г., доцент кафедры СВЧ и КР Фатеев А.В.

2012

УДК 53.17 + 53.08

Рецензент: кандидат физ.-мат. наук, доцент кафедры радиофизики Научного исследовательского Томского государственного университета Буянов Ю.И.

Гошин Г.Г., Фатеев А.В.

Измерение ε и tgδ диэлектрических материалов резонаторным методом: Руководство к лабораторной работе. — Томск: Томский гос. ун-т систем упр. и радиоэлектроники, 2012. — 14 с.

В руководстве содержится методический материал по измерению ε и tgδ диэлектрических материалов резонаторным методом. Отмечаются основные теоретические положения, расчётные формулы, математическую модель эксперимента, входной и выходной тестовый контроль, схемы лабораторных столов и порядок проведения эксперимента, шаблон отчёта, особенности работы программы управления прибором, порядок работы с прибором.

Руководство рекомендовано к выполнению лабораторной работы по дисциплине «Микроволновая техника» по направлению подготовки 210400.68 – «Радиотехника» различных форм обучения.

Гошин Г.Г., 2012

Фатеев А.В., 2012

Томский гос. ун-т систем управления и радиоэлектроники, 2012

		3
	Содержание
1.	Введение...............................................................................................................	4
2.	Краткие теоретические сведения ........................................................................	4
	2.1. Структура поля в цилиндрическом объёмном резонаторе ........................	4
	2.2. Основные параметры объёмного резонатора..............................................	6
	2.3. Расчёт диэлектрической проницаемости и потерь в диэлектрике.............	8
3.	Экспериментальная часть....................................................................................	9
	3.1 Описание установки и методики измерений ...............................................	9
	3.2 Порядок выполнения работы .....................................................................	10
4.	Домашнее задание..............................................................................................	13
5.	Содержание отчёта.............................................................................................	14
6.	Список литературы ............................................................................................	14

1. Введение

Целью лабораторной работы является:

ознакомление с некоторыми вопросами теории объёмных цилиндрических резонаторов;

расчёт основных параметров цилиндрического резонатора для колебаний типа E и типа H , возбуждаемых в резонаторе;

изучение методики измерений, основанной на методе малых возмущений, применительно к цилиндрическому резонатору;

проведение измерений образцов различных диэлектрических материалов.

2.Краткие теоретические сведения

2.1.Структура поля в цилиндрическом объёмном резонаторе

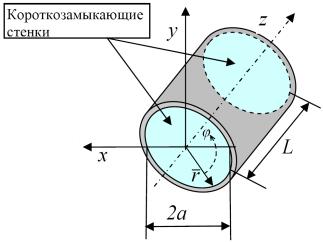
В радиотехнике сверхвысоких частот в качестве колебательных систем используются замкнутые металлические объемы, называемые объемными резонаторами. Замкнутый объем образован стенками волновода и короткозамыкающими металлическими пластинами на его торцах (рис. 1). В лабораторной работе используется цилиндрический объемный резонатор с возбуждением посредством петли.

Рисунок 1 – Цилиндрический объёмный резонатор.

Одним из основных отличий объемного резонатора от колебательного контура с сосредоточенными параметрами является его многомодовость. Объясняется это тем, что в резонаторе, как и в волноводе, могут возбуждаться продольные магнитные и продольные электрические типы колебаний (моды), но в отличие от волноводов, кроме вариаций полей по поперечным координатам и r имеются вариации и по оси z, совпадающей с осью резонатора (рис. 1). Каждый тип колебания характеризуется собственной структурой поля и собственной резонансной частотой f0. Под структурой понимают распределение и форму электрических и магнитных силовых линий в резонаторе в фиксированный момент времени. Структуру поля можно построить, пользуясь выражениями для компонент векторов E и H , полученными путем решений уравнений Максвелла в

цилиндрической системе координат для короткозамкнутого с двух торцов отрезка круглого волновода.

Выражения, определяющие структуру поля колебаний Hmnp и Emnp в цилиндрическом объёмном резонаторе, имеют следующий вид [1]:

колебания Hmnp

mD J

sin m sin

;

D J

cos m sin

;

0 a

D J

cos m cos

;

(1)

1 m p

D J

sin m cos

;

D J

cos m sin

;

колебания Еmnp

mC J

sin m cos

;

C J

cos m

cos

;

0 0

C J'

cos m sin

;

(2)

1 m p

sin m sin

;

C J

cos m cos

;

где m = 0,1,2,… – число вариаций поля по координате φ;

n = 1,2,… – число вариаций поля по радиусу r;

p = 0,1,2,… – число вариаций поля по оси z;

mn –

n-ый корень производной функции Бесселя Jm

( r) порядка m;

mn –

n-ый корень функции Бесселя Jm

( r) порядка m;

0 2 f0 –

угловая резонансная частота;

μ0 = 4π·10-7 Гн/м – магнитная постоянная вакуума;

ε0 =8,84·10-12 Ф/м – электрическая постоянная вакуума.

Несколько первых значений этих корней приведены в таблице 1.

Таблица 1 – Значения корней функции Бесселя и её производной

		μmn					νmn
n	1		2	3	n	1		2	3
m					m

0	3,832		7,016	10,174	0	2,405		5,52	8,654
1	1,84		5,335	8,536	1	3,832		7,016	10,173
2	3,054		6,705	9,965	2	5,135		8,417	11,620

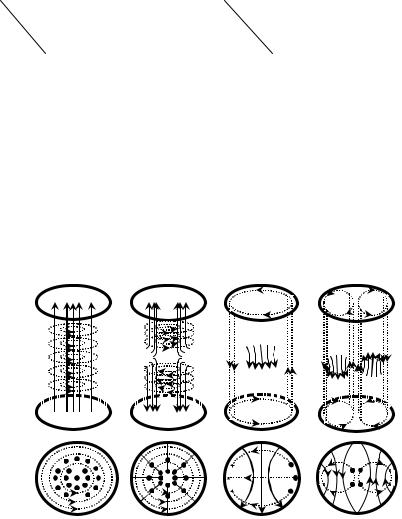
Как следует из уравнений (1) и ( 2), каждая компонента поля в резонаторе зависит от трех координат , r, z . В нем возбуждаются только такие колебания, у которых на определенной резонансной частоте вдоль координатных линий укладывается целое число полуволн. Структура поля для нескольких низших типов колебаний приведена на рисунке 2.

Е010

Е011

Н111

Н211

………………Линии поля Н

____________Линии поля Е

Рисунок 2 – Структура поля в цилиндрическом резонаторе для колебаний типа Нmnp и Еmnp.

2.2.Основные параметры объёмного резонатора

Основными параметрами объёмного резонатора, представленного эквивалентным колебательным контуром на определённом типе колебаний, являются:

резонансная частота f0 или резонансная длина волны 0 c / f0 , где

с = 3·108 м/с – скорость света в вакууме.

собственная добротность резонатора Q0, определяющая его качество как колебательного контура.

Резонансная частота Резонансные частоты определяются по формулам [2]:

f0H = c

f0Å = c


	mn		2		p 2
				+		,

a					L

mn		2			p 2
				+		,
a
					L

где а – радиус резонатора;

L – высота (осевая длина) резонатора.

(3)

(4)

Добротность цилиндрического резонатора Собственные добротности цилиндрического резонатора для колебаний ти-

па Нmnp и Еmnp рассчитываются по методике, изложенной в [3]. Если стенки резонатора и диэлектрик не обладают магнитными свойствами, то искомое выражение имеет вид:

2		Hmnp2 dV
2		V0
Q0			,	(5)
Q0	0	Hmnp2 dS	,	(5)
		S
где 0 – толщина скин-слоя или глубина проникновения поля в корпус				резо-
натора (для латуни 0 127 f0 1 2 мм);

V0 – объем резонатора без диэлектрика;

S – площадь основания резонатора.

После нахождения интегралов формулы для собственной добротности резонатора на колебаниях Нmnp и Еmnp примут вид:

Q H mnp		1
0		0

					m		2					p		2 a 2
		aL 1							1


						mn							mn			L
						mn							mn						, (6)
		p	2	am 2							p		2		a	2		m 2	, (6)
L	1							2								a	1
L	1	2		L				2								a	1	2
		2		L											L			2
		mn								mn								mn

Q0Emnp	1	aL	.	(7)
Q0Emnp	0	L 2a	.	(7)
		L 2a

Нагруженная добротность определяется как

Qн	f0	,	(8)

	fн

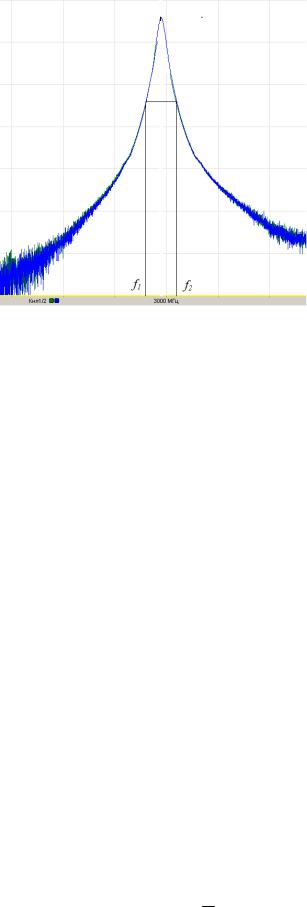
где fí ( f2 f1) – полоса частот резонатора на уровне -3дБ (рис. 1.3).

Рисунок 3 – Резонансная кривая колебания Е010.

2.3.Расчёт диэлектрической проницаемости и потерь в диэлектрике

Диэлектрическая проницаемость образца диэлектрика цилиндрической формы рассчитывается по формуле [4]:

	f	E2dV
1 2		V0
	f0	E2dV ,	(9)

где f f0 f – смещение резонансной частоты при внесении диэлектрика, Vε – объем исследуемого диэлектрика.

Рассмотрим резонатор цилиндрической формы с осесимметричным колебанием E010, имеющим продольную компоненту Ez. Электрическое поле на оси резонатора постоянно и не зависит от φ (см. рис. 2), имеет там максимальное значение напряжённости электрического поля E0, определяемое подводимой мощностью, и достигает нулевого значения на стенке резонатора в силу выполнения граничного условия J0 ( a) 0.

Помещая в резонатор высотой L и радиусом a вдоль его оси образец в виде тонкого цилиндрического стержня радиуса b и высотой h, можно считать, что при выполнении условий b a и L = h поле в образце будет однородным. Необходимо только, поместив образец на дно резонатора, как можно точнее его спозиционировать, совместив оси образца и резонатора, чтобы не нарушить симметрию. Тогда при расчете можно использовать метод малых возмущений [4]. Его применение оправдано при выполнении условия

b a10 . (10)

Взяв интеграл по объёму резонатора и по объёму диэлектрика, для колебания E010 получим:

1 2

a2L f

J12 01

(11)

b2h

0 J2

где 01 2,405 – первый корень производной функции Бесселя нулевого

порядка;

a2L

– отношение объёма пустого резонатора к объему исследуемого

b2h

диэлектрика.

Тангенс угла диэлектрических потерь для колебания типа Е010 рассчитывается по формуле [4]:

	J2	01	L a		2	1	1
tg	1	01						,	(12)
tg							Q
				h b	Q		Q
							0

где Q – добротность резонатора с помещенным в него образцом.

3.Экспериментальная часть

3.1Описание установки и методики измерений

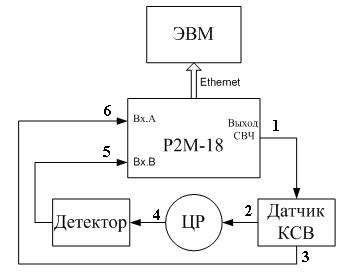
На рисунке 4 приведена структурная схема экспериментальной установки, включающая программно-управляемый измеритель модуля коэффициента передачи и отражения Р2М-18 диапазона до 18 ГГц. Приведённая схема предполагает проведение измерений коэффициента прохождения.

Рисунок 4 – Структурная схема установки для измерения электродинамических параметров резонатора.

На высокочастотном выходе измерителя формируется сигнал и поступает на датчик КСВ. Датчик КСВ содержит в своем составе широкополосный

1 / 21 2 > Следующая >>>

Соседние файлы в папке лаб.раб

#
11.05.20151.01 Mб33633-izmer_dielictrich_mater.pdf
#
11.05.20151.52 Mб32704-skalyr_analiz_parametrov.pdf
#
11.05.2015462.02 Кб30ГГГ-ЛабРабИзмДН и вх.сопр.ант.-2011.pdf
#
11.05.2015327.82 Кб33ИССЛ_ФЕРР.ЦИРК 2011.pdf
#
11.05.2015614.47 Кб32ЛабДиэлАнт_Г 2011.pdf
#
11.05.2015230.79 Кб33ЛабКУ_Г 2011.pdf