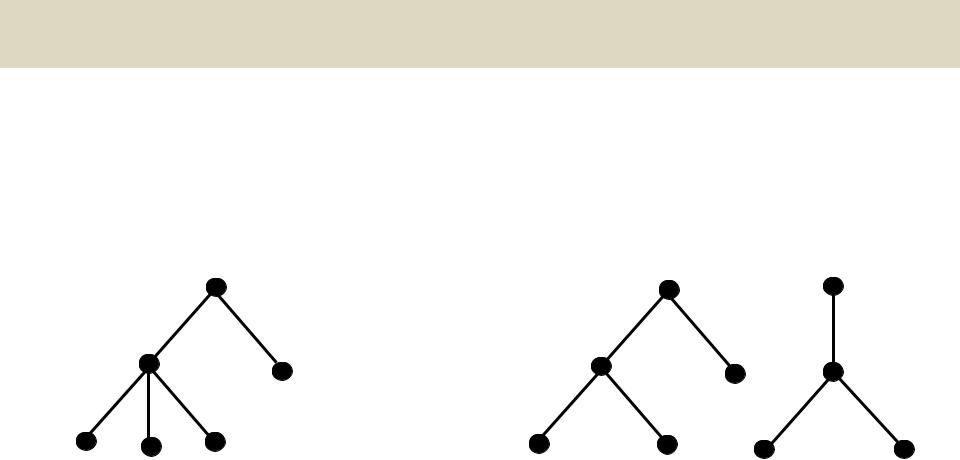
Графы без циклов

G X ,U

X

n,

U

m

Дерево - связный граф

Лес - несвязный

без циклов

граф без циклов

Термины:

Каждая компонента

корень,

лист,

связности леса есть

дерево

G X ,U

Свойства деревьев

X n, U m

2

G Т m G n G 1 и k G 1

3

G Т x, y X

! простая цепь x, y

один лист

2

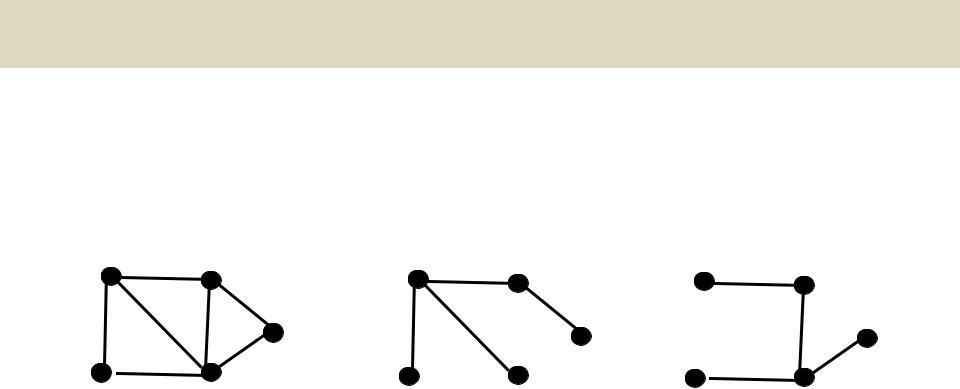
G X ,U

Остов графа

X

n,

U

m

G X ,U

Код дерева

X

n,

U

m

Шаг 1

X x1, x2 , , xn

Найдем

b1 min x

(x X )

p( x) 1

u1 b1, c1

! u1 U :

Запомним номер вершины

c1

Удалим из дерева вершину

b1

и ребро u1

X : X \ b1

U : U \ u1

Шаг 2

Найдем b2 min

x

(x X )

p( x) 1

u2 b2 , c2

! u2 U :

Запомним номер вершины

b2

c2

u2

Удалим из дерева вершину

и ребро

X : X \ b2

U : U \ u2

Шаг n-2

min

(x X )

Найдем bn 2

x

p( x) 1

un 2

bn 2 , cn 2

! un 2 U :

Запомним номер вершины

cn 2

Удалим из дерева вершину

bn 2 и ребро

un 2

X : X \ bn 2

U : U \ un 2

Код дерева

U un 1

C(T ) c , c

, ,

c

n 2

1 2

X x1, x2 , , xn

C(T ) c1, c2 , ,

cn 2

Цикл пока C(T )

Найти b min

x

(x X )

x C(T )

(c C(T ))

c первая вершина кода

Построить ребро

u b, c

С : С \ с

X : X \ b

X x , x

, , x

n

C(T ) c , c

, , c

n 2

1 2

1 2

Теорема Количество помеченных

nn 2

деревьев с n вершинами равно

Количество кодов равно

nn 2