1.2 Бинарные отношения

1.2.1 Декартово произведение множеств. Соответствие множеств

Декартовым произведением двух множеств X и Y называется множество всех упорядоченных пар ( x,y ) таких, что , а .

Пример 1. Пусть .

Тогда , .

Очевидно, что , т.е. операция декартова произведения множеств не является коммутативной.

Декартовым произведением множеств называется множество всех упорядоченных наборовтаких, чтоЕсли, то декартово произведение обозначают.

Будем говорить, что задано соответствие q между множествами X и Y, если задана упорядоченная тройка , где.Множество X называется областью отправления, а Y – областью прибытия соответствия q (обозначают ). Каждый элементy в паре называется образом элементаx (x – прообразом элемента y) при данном соответствии q.

Соответствие называетсяотображением множества X во множество Y, если каждый элемент имеет образ, т.е..

Отображение называетсяфункциональным, если каждый элемент имеетединственный образ :. Множество образов при данном отображенииобозначается:.

Если множество совпадает с множествомY, то говорят, что осуществляет отображениена множество Y.

Соответствие называетсявзаимно однозначным (биекцией), если а) является отображением; б) функционально; в) отображает X «на» множество Y; г) из условия следует .

Другими словами, является биекцией, если каждый элементимеет единственный образ, а каждый элементимеет единственный прообразпри данном отображении:

(1.2)

1.2.2 Определение бинарного отношения

Определение. Говорят, что на множестве X задано бинарное отношение R, если задано подмножество декартова произведения (т.е. ).

Пример 2. Пусть Зададим наХ следующие отношения:

–отношение равенства;

–отношение предшествования;

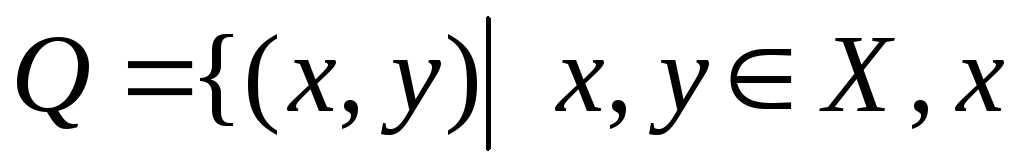делится на – отношение делимости.

Все эти отношения заданы с помощью характеристического свойства. Ниже перечислены элементы этих отношений:

Тот факт, что пара (x, y) принадлежит данному отношению R, будем записывать: или xRy. Например, для отношения Q запись 4Q2 означает, что 4 делится на 2 нацело, т.е.

Областью определения бинарного отношения R называется множество Областью значений называется множество

Так, для отношения Р из примера 2 областью определения является множество , а областью значений –.

1.2.3 Способы задания бинарного отношения

Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Более наглядными способы задания бинарного отношения являются график отношения, схема отношения, граф отношения, матрица отношения.

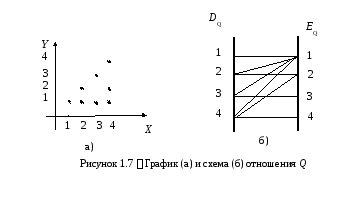
График отношения изображается в декартовой системе координат; на горизонтальной оси отмечается область определения, на вертикальной – множество значений отношения; элементу отношения (х,у) соответствует точка плоскости с этими координатами. На рис. 1.7,а) приведен график отношения Q примера 2.

Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (х,у) принадлежит отношению R, то соответствующие точки из и соединяются отрезком прямой. На рис. 1.7,б) приведена схема отношения Q из примера 2.

Граф отношения строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множестваХ. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара ( х,у ) принадлежит отношению R. На рис. 1.8,а) приведен граф отношения Q примера 2.

Пусть . Матрица отношения имеет n строк и n столбцов, а ее элемент определяется по правилу:

На рис.1.8,б) приведена матрица отношения Q примера 2.