Группа подстановок
Опр. Множество G c введенной на нем алгебраической операцией называется
группой, если
1) a,b,c G a b c a b c
2) e G : x G |
|
|
|
|
|
|
|
x e e x x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) x G x G : |
|
|
|
|
x x |
|
x x e |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- нейтральный элемент (единица) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
- симметричный элементу х (обратный) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У1. В группе существует единственный нейтральный элемент
У2. У каждого элемента х существует единственный симметричный элемент 1
Группа подстановок
Примеры |
1) |
|
Z, |
|
2) |
|
R \ |
|
0 , |
3) S |
n |
, |
|
|
|
|
|
|
|
||||||
групп |
4) группа движений плоскости |
|||||||||||
5) группа симметрии правильного n - угольника
Опр. Порядком конечной группы называется количество ее элементов
|
|
B |
|
|
|
|
|
|
|
|
|
|
0 |
|
поворот |
на 0 |
|
III |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
I |
|
|
|
|
|
|
|
1 |
поворот |
на 120 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A |
|
|
|
C |
|
|
|
|
|
|
|
2 |
|
поворот |
на 240 |
||
|
II |
|
|
|
|
|
|
|
|
3 |
|
отражение |
(I) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отражение |
(II) |
|
0, |
|
1, |
|
2, |
|
3, |
|
4, |
|
5 |
4 |
|
отражение |
(III) |
|||
|
|
|
|
|
|
5 |
|
|
|
2 |
|||||||
|
|
1 2 3 |
||
|
|
|
|
|
|
0 |
|
|
|
|
|
1 2 3 |
||
|
|
1 2 |
3 |
|
|
|
|
|
|
|
1 |
|
2 3 |
|
|
|
1 |
||
|
|
1 2 |
3 |
|
|
|
|
|
|
|
2 |
|
3 1 |
|
|
|
2 |
||
Группа подстановок
Таблица Кэли группы S3
0 1 2 3 4 5
0 |
0 1 2 3 4 5 |
|||||||
1 |
1 2 0 |
4 |
5 |
3 |
||||
2 |
2 |
0 |
1 |
5 |
3 |
4 |
||
3 |
3 |
5 |
4 |
|
0 2 |
1 |
||
4 |
4 |
3 |
5 |
1 |
0 |
2 |
||
5 |
5 |
4 |
3 |
2 1 |
0 |
|||
|
|
1 2 3 |
|
|
|
1 2 3 |
|
|
|
1 2 3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
1 3 2 |
|
4 |
|
3 2 1 |
|
5 |
|
|||
|
|
|
|
|
|
|
|
2 1 3 |
|||||
3
Изоморфизм групп
Опр. Группы G1, |
и G2 , называются |
|
изоморфными, |
если существует биекция |
|
G1 на G2 , сохраняющая групповую |
||
f x y |
f x f y |
|
операцию |
|
|
У3. При изоморфизме образом нейтрального элемента группы G1 является
нейтральный элемент группы G2
У4. При изоморфизме образом элемента, симметричного данному, является элемент, симметричный образу данного
4
Изоморфизм групп
Опр. Множество H G называется подгруппой группы G, , если
1) оно замкнуто относительно |
|||
2) e Н |
~ |
~ |
~ |
3) x Н |
x |
Н : x x |
x x e |
Теорема Кэли. Всякая конечная группа |
|
порядка n изоморфна некоторой подгруппе |
|
группы подстановок Sn |
|
G, , G n |
|
F Sn : G, |
F , 5 |
Группы движений плоскости
Опр. Движением называется преобразование евклидова пространства, при котором расстояние между любыми двумя точками не меняется
Теорема. Всякое движение на плоскости является одним из следующих отображений:
1) поворот (в т.ч. центральная симметрия и тождественное отображение),
2)параллельный перенос,
3)осевая симметрия,
4)композиция поворота и
параллельного переноса, 5) композиция осевой симметрии и
параллельного переноса. 6
Группы движений плоскости
Группа движений плоскости, имеющих
неподвижную точку
-сохраняется скалярное произведение векторов
Группа вращений и группа симметрии правильного n - угольника
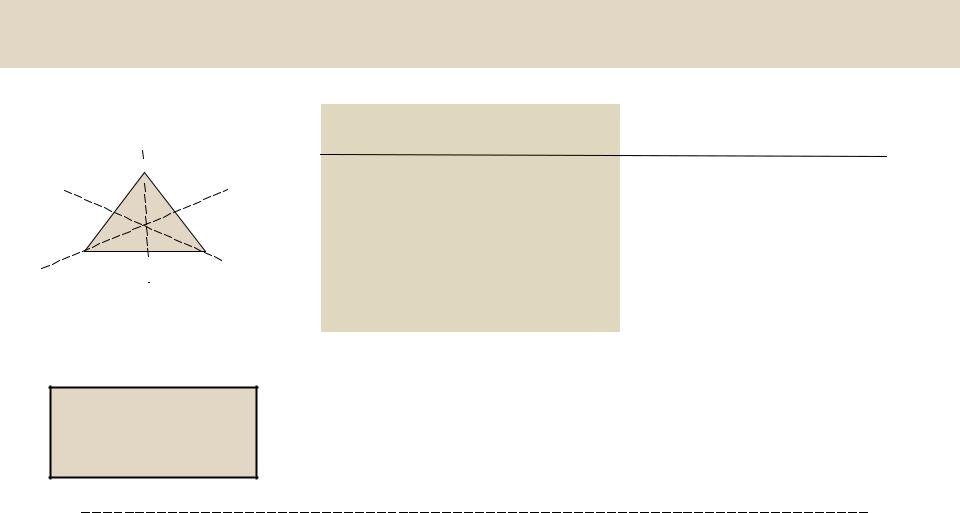
Группа симметрии правильного треугольника
|
B |
0 |
|
поворот |
на 0 |
|
|
||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
III |
I |
1 |
поворот |
на 120 |
|
||||
|
|
||||||||
A |
C |
2 |
|
поворот |
на 240 |
||||
3 |
|
отражение |
(I) |
|
|||||
|
II |
|
|||||||
|
4 |
|
отражение |
(II) |
|||||
G 0, 1, 2, 3, 4, 5 |
|||||||||
5 |
|
отражение |
(III) 7 |
||||||
Группы симметрии геометрических фигур
Таблица Кэли.
B
III |
I |
A 
C
II
G 
S3
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
1 |
1 |
2 |
0 |
4 |
5 |
3 |
2 |
2 |
0 |
1 |
5 |
3 |
4 |
|
|
|
|
0 |
2 |
1 |
3 |
3 |
5 |
4 |
|||
4 |
4 |
3 |
5 |
1 |
0 |
2 |
5 |
5 |
4 |
3 |
2 |
1 |
0 |
S |
|
|
|
|
|
|
|
1 2 3 |
|
|
|
|
|
|
1 2 3 |
|
|
|
|
1 2 3 |
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
1 2 3 |
|
|
|
|
2 3 1 |
|
|
|
3 1 2 |
||||||||||
|
|
1 2 3 |
|
1 2 3 |
|
|
1 2 3 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
1 3 2 |
|
4 |
|
3 2 1 |
|
|
5 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 1 3 |
|
8 |
|
|||||||||||
Группы симметрии геометрических фигур
Циклические |
Сn e, 1,..., n 1 |
|
|
||||||
группы |
Сn n |
|
|
2 |
|
|
k 1, n 1 |
||
|
|
|
k |
n |
|
k , |
|
||
|
|
Dn |
|
|
|
|
|
||
Диэдральные |
e, 1,..., n 1, |
1,..., n |
|||||||
группы |
Dn 2n |
(n 1 отрезок, |
n 2 |
ромб) |
|||||
|
|
|
|
D1 С2 |
|
|
D2 |
|
V |
|
|
|
|
III |
|
|
|
|
|
|
B |
|
|
V |
C |
|
|
|
D |
III |
I |
|
|
B |
|
|
|
|
E |
|
|
|
|
|
|
|
|
||
|
|
|
|
II |
|
|
|
|
|
A |
C |
|
|
IV |
A |
|
|
|
F |
С3 3 |
II |
|
|
D6 12I |
|
|
|
|
|
D3 |
S3 |
|
|
|
VI |
9 |
|||
Группы симметрии геометрических фигур
Движения в пространстве, сохраняющие неподвижную точку
1)центральная симметрия (относительно точки),
2)осевая симметрия (относительно прямой),
3)зеркальная симметрия (относительно плоскости)
|
Т - группа вращений тетраэдра |
|
T |
|
12 |
|||||||
|
|
|
||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
AO (BCD) |
0 |
|
поворот на 0 |
|
|||||
|
|
|
|
|||||||||
B |
|
|
|
(4оси 2 8) |
1 |
|
поворот на 120 |
|||||
M |
O |
|
C |
2 |
|
поворот |
на 240 |
|
||||
|
|
|
||||||||||
|
|
|
|
|
||||||||
|
D |
MN BD, MN AC |
9 |
поворот |
|
на 180 |
||||||
BM MD, AN NC |
(3оси 1 3) |
10 |