Архив ZIP - WinRAR_1 / 33) теорема о циркуляции вектора магнитно индукции

1. Теорема о циркуляции вектора магнитной индукции.

- теорема о циркуляции вектора :

циркуляция вектора по произвольному контуру равна произведению на алгебраическую сумму токов, охватываемых контуром.

; ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (рис. 44).

Теорема о циркуляции доказывается посредством закона Био-Савара-Лапласа и подтверждается экспериментально.

Для распределенного по объему тока

,

.

поле не потенциально (в отличие от электростатического поля); магнитное поле - вихревое (соленоидальное или трубчатое) поле, свободное от источников (следует из равенства нулю дивергенции).

Соответствующие трубки называются трубками тока; где трубка сжимается, там значение вектора увеличивается (аналогично изменению скорости течения при изменении проходного сечения; поток во всех сечениях одинаков).

В пределе при

- ротор поля (вихрь вектора).

Здесь проекция ротора на направление нормали к плоскости контура, по которому берется циркуляция.

,

ротор получается в результате векторного перемножения оператора Гамильтона и вектора магнитной индукции ().

- теорема Стокса.

Направление ротора определяется по направлению нормали , где .

.

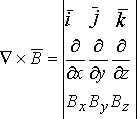- дифференциальная форма теоремы о циркуляции .

Для электростатического поля

поле потенциально вектор напряженности можно представить в виде градиента скалярной функции (потенциала ).

поле соленоидально вектор магнитной индукции можно представить (как и всякий соленоидальный вектор) как вихрь некоторого другого вектора () ,

где - векторный потенциал.