1.5.1. Эффект Холла

Метод измерения концентрации и подвижности носителей заряда с помощью эффекта Холла получил широкое применение. Физическая сущность эффекта Холла заключается в следующем.

Предположим, что электроны в зоне проводимости полупроводника движутся, находясь под одновременным воздействием

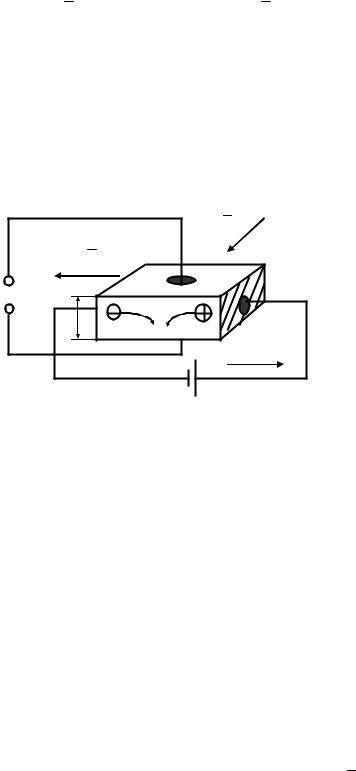
электрического поля Ex , магнитного поля Bz и какого-то достаточно эффективного механизма рассеяния. (Принципиальная схема метода измерений приведена на рис. 1.9.) Сила Лоренца, действующая на носители , движущиесязаряда в электрическом поле с дрейфовой скоростьюvдр, определяется формулой

Bz

Ex

Рис. 1.9. Схема для исследования эффекта Холла

Для дырок векторное произведение и сила Лоренца в данном случае будут направлены вниз, для электронов векторное произведение направлено вверх, а сила Лоренца— вниз. Следовательно, как дырки, так и электроны будут отклоняться магнитным полем на нижнюю грань, а верхняя грань будет обедняться в пер-

и возникает холловское ,поленаправленное снизу вверх. В полупроводнике n-типа нижняя грань (при том же направлении тока) заряжается отрицательно, верхняя — положительно и холловское поле направлено сверху вниз. Величина поля растет до тех пор, пока не скомпенсирует силу Лоренца и поперечный ток не станет равен нулю. При этом результирующее поле E будет по-

16

вернуто относительно Ex на некоторый угол jH , пропорциональ-

ный магнитной индукции Bz :

Если зона проводимости может быть охарактеризована изотропной скалярной эффективной массой, то с помощью кинетического уравнения Больцмана можно прийти к соотношению

Холловское поле пропорционально плотности продольного тока J x и напряженности магнитного поля Bz . Его величину находят, измеряя холловское напряжение VH:

В соответствии с этой моделью постоянная Холла(которая определяет величину отклика в направлении, перпендикулярном как току, так и полю) равна

фактором. Она зависит от комбинации процессов рассеяния, эффективных в заданных условиях, и от того, как меняется среднее время между столкновениями с энергией электрона. Как правило, холл-фактор по величине близок к единице. Так, r = 1, если все электроны движутся с одинаковой скоростью, как это предполагается в классической модели Друде или для вырожденного электронного газа (в котором все электроны движутся с одинаковой

подвижностью. Для некоторых полупроводников оказалось возможным измерить дрейфовую подвижность независимым мето-

17

и электроны, и дырки смещаться в одном и том же направлении. Поэтому вклады электронов и дырок в эффект Холла стремятся скомпенсировать друг друга (см. рис. 1.9), так что

Как следует из приведенных выше соотношений, для определения концентрации и подвижности носителей заряда необходимо измерить электропроводность образца и постоянную Холла.

Измерения эффекта Холла сопровождаются рядом физических явлений:

1)появлением температурного градиента в направлении, совпадающем с направлением холловского поля(эффект Эттингаузена);

2)возникновением поперечной разности потенциалов в -на правлении холловского поля при наличии температурного градиента, совпадающего с направлением тока (эффект Нэрнста — Эттингаузена);

3)появлением поперечного градиента температуры в - на правлении холловского поля при наличии температурного градиента, совпадающего с направлением тока (эффект Риги — Ледюка);

4)возникновением дополнительной разности потенциалов между холловскими зондами вследствие их несимметричного расположения.

Перечисленные источники ошибок устраняют измерениями при разных полярностях тока и магнитного поля. Чтобы избежать случайных ошибок при измерении холловской разности потенциалов за счет контактных, связанныхявлений с наличием больших контактных сопротивлений, рекомендуется применять вольтметры с большим входным сопротивлением.

Приведенные выше формулы для эффекта Холла справедливы при слабых магнитных полях, удовлетворяющих условию

mH Bz << 1. На практике обычно используют поля с индукцией до

1,0 Тл. Для повышения точности измерений необходимы хорошая стабилизация магнитного поля и его однородность.

Источником ошибок может служить погрешность в определении геометрических размеров образца и расстояния между зондами. Поэтому для повышения точности измерений контакт дела-

ют малой площади. Реализуемая на практике случайная погрешность измерений лежит в пределах5–10 % при доверительной вероятности 0,95.

18

Для измерения эффекта Холла классическим методом необходимо изготовление образцов правильной геометрической формы, что является достаточно трудоемким и не всегда приемлемым процессом.

Для измерения на тонких образцах и эпитаксиальных структурах используют метод Ван дер Пау (см. рис. 1.3).

При определении постоянной Холла токI подводится через зонды 1 и 3. Между другой парой контактов 2 и 4 измеряют падение напряжения. Для этой конфигурации контактов постоянная Холла равна

где DU24 — изменение напряжения между зондами2 и 4 после

включения магнитного поля; k — поправочный коэффициент, учитывающий геометрию образца (табл. 1.3). Затем повторяют измерения, изменив назначение контактов: через 2 и 4 подают ток I24, а с 1 и 3 снимают разность напряжений DU13 . По этим данным оп-

ределяют RH 13,24 , RH 24,13 . Истинная постоянная Холла находится как среднее арифметическое RH 13,24 и RH 24,13 :

Для точного измерения электропроводности и постоянной Холла при каждом значении тока необходимо сделать четыре измерения s и восемь — для RH, а полученные данные усреднить.

Таблица 1.3 Значения коэффициентов k для случая размещения зондов, как

на рис. 1.3 (прямоугольный образец)

1.5.2. Метод вольт-фарадных характеристик барьера Шоттки

Метод является основным при контроле концентрации носителей заряда в эпитаксиальных слоях, выращенных на сильнолегированной или полуизолирующей подложках. Принцип метода следует из основных положений теории барьера Шотткиp-n-и перехода и основан на определении зависимости емкости барье-

19

ра Шоттки иp-n-перехода от напряжения смещения. Емкость барьера Шоттки обусловлена наличием области объемного заряда, возникающей в результате обеднений ее свободными носителями под действием внутреннего и внешнего электрических -по лей.

Ширина области объемного зарядах связана с емкостью

где А — площадь барьера; e0 — диэлектрическая проницаемость вакуума; e — относительная диэлектрическая проницаемость материала.

С другой стороны, емкость барьера, по определению, для полупроводника n-типа

где I(t) — ток, обусловливающий изменение заряда Q на емкости

C.

Комбинируя (1.32) и (1.33), получаем для концентрации свободных носителей

Таким образом, измеряя зависимость емкости барьера от напряжения смещения U, можно с помощью формулы (1.34) вычислить концентрацию свободных носителей N(x), которая для неоднородного полупроводника зависит от глубиныx, на которую проникает объемный заряд. Производную в формуле (1.34) обычно определяют графическим дифференцированием экспериментальной зависимости величины1/С2 от U по методу конечных приращений. Поэтому на практике пользуются расчетной формулой

Формула (1.34) получена для наиболее общего случая произвольного распределения примесей по объему исследуемого -об

20

x = 2ee0 A (C1 + C2 ).

Случайная погрешность метода складывается главным образом из погрешностей измерения величин, входящих в расчетную формулу (1.35). Случайная погрешность в определении концентрации рассчитывается по следующей формуле:

где D — диаметр диодной структуры; g = DCC .

Первый член этого соотношения определяет погрешность измерения диаметра диодной структуры, второй — погрешность,

связанную с измерением наклона, D (1C2 ), DU . При этом ошибки

в измерении напряжения не принимаются во внимание, так как предполагается, что точность отсчета напряжения может быть очень высокой. Погрешность измерения площади барьера зависит от способа его и размеров. На практике барьеры Шоттки изготовляют напылени-

ем или электролитическим осаждением металлов на поверхность исследуемого полупроводника. В некоторых случаях проводят поверхностную диффузию для созданияp-n-перехода, а затем c помощью химического травления создают диодную структуру.

Для создания барьера Шоттки широко используется ртутный контакт. Применение ртутного контакта значитель упрощает подготовку образца к измерению. Его использование вносит дополнительную ошибку в погрешность измерений концентрации. Эта ошибка носит и систематический, и случайный характер, причиной ее появления служит то обстоятельство, что пло-

натяжение ртути очень велико, свободная поверхность ртути в капилляре при его контакте с измеряемым образцом образует по краям выпуклый мениск. Поверхность образца, смачиваемая ртутью, будет меньше площади геометрического сечения капилляра. С увеличением давления в ртутном капилляре радиус кривизны мениска увеличивается, и площадь смачиваемой поверхности образца возрастает, приближаясь к площади сечения капилляра.

При работе с ртутью необходимо строго соблюдать соответствующие требования техники безопасности. Поэтому стараются использовать другие жидкометаллические контакты, например галлий-цинк или индий.

21

Из особенностей функцииC = ƒ(U) барьера Шоттки cледует, что источником систематической погрешности является допускаемая на практике аппроксимация точного выражения(1.35)

распределения примесей по толщине эпитаксиального слоя эта погрешность очень мала и составляет доли процента. При возрастании концентрации свободных носителей в направлении от барьера рассматриваемая систематическая погрешность уменьшается. Если концентрационный профиль имеет спадающие функции, то тогда эта погрешность больше, чем при однородном распределении. Кроме ошибок, следующих из расчетной формулы (1.35), существует еще ряд источников погрешности измерений концентрации носителей заряда:

1)краевой эффект, который наиболее сильно проявляется при измерении высокоомных образцов с малым диаметром диодной структуры. Влияние этого эффекта можно ограничить, увеличив площадь измеряемого объекта;

2)токи утечки барьера, возникающие обычно при больших смещениях и при измерениях на сильнолегированных образцах;

3)фотоэлектрические явления на барьере Шоттки. Для устранения этой погрешности измерения рекомендуется проводить в затемненной камере;

4)отклонение свойств реального барьера от модели резкого перехода.

На основе этого метода выпускаются профилометры — измерители профиля распределения концентрации в тонких эпитаксиальных слоях. В основе работы профилометра лежит способ из-

мерения емкости барьераC-электролит-полупро- водник с одновременным травлением этим электролитом локальной области полупроводниковой структуры, и по известному соотношению определяется концентрация N носителей заряда

где Vd — диффузионный потенциал; е — заряд электрона; er — диэлектрическая проницаемость полупроводникового материала;

22

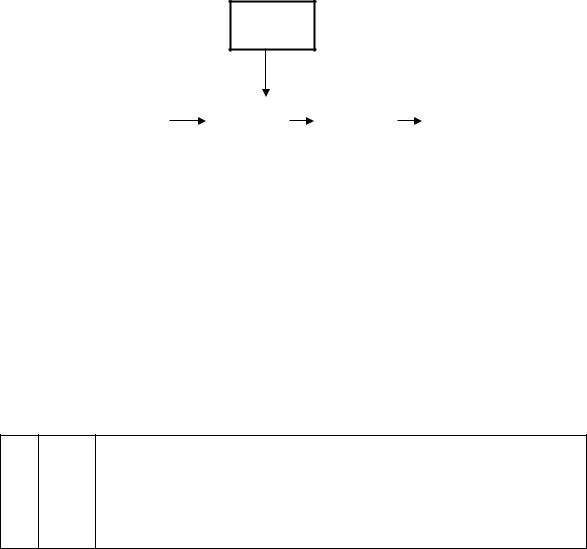
При травлении полупроводникового материала барьер смещается вглубь, и при непрерывном измерении электрической емкости контакта возможно определить распределение концентрации по глубине. Травитель для GaAs имеет следующий состав: H2SO4:6H2O2:3H2O при рекомендуемом соотношении100:600:300 мл. Структурная схема профилометра представлена на рис. 1.10. От генератора синусоидальных колебаний1 напряжение с частотой 10 кГц и 50 мВ поступает на исследуемый образец2, к которому с помо-

щью насоса 5 подается травящий раствор. На вход индикаторного устройства 3 поступает напряжение, амплитуда которого пропорциональна величине емкости барьера электролит-полупроводник. После усиления, логарифмирования и детектирования сигнал поступает на самопишущий в виде постоянного напряжения, амплитуда которого пропорцио-

нальна концентрации носителей заряда в полупроводниковом материале.

5

Рис. 1.10. Структурная схема профилометра: 1 — генератор синусоидальных колебаний; 2 — исследуемый образец; 3 — индикаторное

устройство; 4 — самописец; 5 — кислотостойкий насос

Определение концентрации носителей заряда производится по градуировочным кривым, которые приводятся индивидуально для каждого профилометра. Пример такой калибровки для структур GaAs при диаметре контакта 3 мм приведен в табл. 1.4.

Таблица 1.4 Калибровочная зависимость концентрации

носителей заряда от электрической емкости контакта электролит-полупроводник

23