
- •Смирнов С.В.
- •1. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ
- •1.5.1. Эффект Холла
- •1.5.2. Метод вольт-фарадных характеристик барьера Шоттки
- •1.5.3. Определение концентрации носителей заряда методом плазменного резонанса
- •1.5.4. Определение концентрации по эффекту Фарадея
- •1.6.1. Измерение дрейфовой подвижности
- •1.6.2. Определение времени жизни носителей заряда
- •1.7.1. Циклотронный резонанс
- •1.7.2. Методы измерения ширины запрещенной зоны
- •2.2.1. Методика измерений эллипсометрических параметров
- •2.3.1. Молекулярные спектры
- •2.3.2. Фурье-спектроcкопия
- •2.3.3. Аналитическое использование электронных спектров поглощения
- •2.3.4. Оптическая электронная спектроскопия в отраженном диффузно рассеянном свете
- •3.7.1. Физические основы
- •4. МАСС-СПЕКТРОМЕТРИЯ
- •4.1.1. Физические основы
- •4.1.2. Аппаратная реализация
- •4.1.3. Основные характеристики и применения
- •6. СПЕКТРОСКОПИЯ ОБРАТНОРАССЕЯННЫХ ИОНОВ
2.3.4. Оптическая электронная спектроскопия в отраженном диффузно рассеянном свете
Оптическая электронная спектроскопия в отраженном диффузно рассеянном свете широко применяется в исследованиях, связанных с выяснением поверхностных состояний дисперсных твердых тел, а также реакций, протекающих на поверхности раздела фаз; велика роль метода в изучении электронного строения твердых тел. В оптический интервал длин волн200–1000 нм попадают переходы валентных электронов с верхних заполненных на нижние вакантные орбитали(состояния практически для всех твердых веществ за исключением широкозонных диэлектриков— например, SiO2, MgO, BaSO4 и др.). Поскольку основные химические и физические свойства обусловлены именно состоянием внешних валентных электронов, становится ясным, что оптические электронные спектры несут наиболее важную и фундаментальную информацию о веществе.
В оптической спектроскопии прозрачных в видимой и- УФ области объектов исходная интенсивность монохроматического излучения I0 и регистрируемая после его взаимодействия с веществом Iрег связаны соотношением
I0 = Iрег +Iпогл +Iотр, |
(2.35) |
где Iпогл и Iотр — поглощенная и отраженная объектом части излучения.
Аналогично этому в спектроскопии диффузного отражения
F0 = Fдиф.отр + Fпогл + Fотр, |
(2.36) |
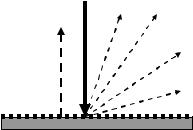
где F0 — интенсивность падающего света; Fдиф.отр — часть излучения, диффузно отраженного от исследуемого образца; Fпогл — часть излучения, поглощенная образцом; Fотр — зеркально отраженная от образца часть излучения (рис. 2.13).
F0 Fдиф.отр
Fотр
Рис. 2.13. Схема отражения света дисперсным твердым веществом
57
В уравнениях (2.35), (2.36) члены Iотр и Fотр представляют собой составляющие, в определенных условиях значительно искажающие спектры. В качестве оптических эталонов обычно используют хорошо отражающие в рабочем диапазоне длин волн белые порошки, например MgO.
Функцией отражения исследуемого образца является нормированная величина, называемая коэффициентом диффузного отражения:
RD = Fдиф.отр /F0. |
(2.37) |
Соответственно поглощающие свойства объекта описываются разностью (1–RD). Оптический спектр в большинстве случаев представляют в виде распределения поl коэффициентов RD или (1–RD). Однако наиболее общим, описывающим случаи бесконечно толстого непрозрачного слоя, является уравнение Кубелки—
Мунка: |
|
F = (1–RD)2/2RD, |
(2.38) |
где F — функция поглощения.
Сравнение спектров стекол в проходящем свете и их спек-
тров диффузного отражения |
в координатахF = ƒ(l) |
иногда |
||
показывает их полное совпадение. В области очень малых кон- |
||||
центраций |
исследуемого |
вещества |
в |
непоглощающем |
разбавителе, а также в области малых уровней заполнения -по |
||||
верхности адсорбированными молекулами, дающими сигнал в |
||||
спектре, функция Кубелки— Мунка |
изменяется линейно от мо- |
|||
лярной концентрации, т.е. она может быть использована для фо- |
||||
тометрического определения.
Однако в случае дисперсных твердых веществ с высокой удельной поверхностью применять ее не удается даже при заполнении сотых долей поверхности от монослоя. Так, на поверхности твердой поликремниевой кислоты(силикагеля)
с удельной поверхностью S0 = 250 м2/г область линейной зависимости функции F от концентрации нанесенного (адсорбированного) хромофора составляет 10–2–10–3 от монослоя. В области больших заполнений приходится сталкиваться с явлением так называемого«оптического насыщения», при котором практически отсутствует зависимость интенсивности поглощения от концентрации исследуемого вещества. Вероятная причина этого явления кроется в многократном отражении-поглощении света развитой поверхностью мелкодисперсного порошканепосредст-
венно в , слоеа кроме , тогов порах
итрещинах частиц.
Вбольшинстве случаев интерес представляет все-таки сам спектр, т.е. положение основных максимумов полос поглощения и
58
их изменение в результате тех или иных превращений вещества. С этой точки зрения, получение и качественный анализ спектров диффузного отражения не вызывают принципиальных трудностей.
Общая теория электронных спектров — обширная и наиболее полно разработанная область спектроскопии. Количественный подход включает проведение квантово-механических расчетов электронного строения и сопоставление полученных значений с экспериментальными.
Коротковолновая часть оптических электронных спектров формируется, как правило, в результате переходов с переносом заряда, которые проявляются в виде широких и интенсивных по-
лос |
на |
краю |
видимой |
и |
в |
основном |
УФ-области. Край полосы в спектрах переноса заряда соответст- |
||||||
вует переходу электронов с верхней заполненной орбитали - ва |
||||||
лентной зоны на нижнюю вакантную орбиталь зоны проводимо- |
||||||
сти. |
Соответствующий |
энергетический |
зазор |
определяется в |
||
физике твердого тела термином«ширина запрещенной зоны». Это фундаментальная характеристика твердого вещества. В случае, когда край полосы в спектре переноса заряда выражен - от четливо, возможно достаточно надежное определение ширины
запрещенной |
зоны DЕg |
графическим |
методо |
из зависимости a2 = ƒ(hn), так как |
|
|
|
|
a = А(hn – DEg)1/2. |
(2.39) |
|
Оценка коэффициента А дает величину |
около104 см–1×эВ1/2. Из |
|
|
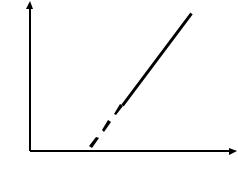
выражения (2.39) следует, что a очень быстро растет с увеличением энергии фотона. Очевидно, что край собственного поглоще-
ния при прямых переходах в коор- a2 |
|
|
||||
динатах |
|
a2 = ƒ(hn) |
будет |
представ- |
|
|
лять собой прямую линию, пересе- |
|
|
||||
кающую |
|
ось |
энергий |
|
||
в точке hn = DEg (рис. 2.14). |
|
|
||||
Коэффициент |
поглощения a |
|
|
|||
рассчитывается по данным измере- |
|
|
||||
ний |
коэффициента |
прозрачности |
DEg |
hn |
||
(коэффициента пропускания) образ- |
Рис. 2.14. Край |
|
||||
ца. Пропусканием Т называется от- |
|
|||||
ношение |
интенсивности |
света, про- собственного поглощения |
||||
шедшего |
через |
образец, к |
|
|
||
интенсивности падающего на образец света. Если толщина образца d много больше длины волны l, то связь между коэффициентом пропускания Т, коэффициентом отражения R и a выглядит следующим образом:
59

|
(1 - R)2 é1 + (la 4pn )2 |
ù |
|
|
ê |
ú |
|
T = |
ë |
û |
, |
|
|
||
|
exp(ad) - R2 ex p(-ad) |
||
где n — показатель преломления материала.
В области изменения прозрачности от(1–R)/(1+R) для пропускания получается более простая формула:
T= (1 - R)2 ex p(-ad) . 1 - R2 ex p(-2ad)
Когда Т < 10 %, формула приобретает вид
(2.40)
до 10 %
(2.41)
T = (1 - R)2 (exp(-ad)), |
(2.42) |
||||
откуда |
|
(1 - R)2 |
|
|
|
a = |
1 |
l n |
. |
(2.43) |
|
d |
|
||||
|
|
T |
|
||
Из выражения (2.46) следует, что для расчета a кроме пропускания необходимо измерить еще и коэффициент отраженияR. Этого можно избежать, если измерить пропускание двух идентичных образцов с несколько различающимися толщинамиd1 и d2. В этом случае
a = [1 (d1 - d2 )] (l g T1 - l g T2 ) . |
(2.44) |
l g e |
|
Величина lgT называется оптической плотностью образца.
2.4. Фотоэлектрическая диагностика квантово-размерных структур
|
Фотоэлектрические явления, возникающие в полупроводнико- |
|
||||
вых квантово-размерных структурах при фотогенерации электро- |
|
|||||
нов |
и |
дырок |
в |
области |
оптического, |
поглоще |
проявляются в виде фотопроводимости и различных фотовольтаи- |
|
|||||
ческих |
эффектов. |
Для |
целей |
диагностики |
квантово-размер- |
|
ных структур особенно удобен метод спектроскопии конденсатор- |
|
|||||
ной фото-ЭДС. |
|
|
|
|
|
|
Спектры фотопроводимости измеряют на образцах планарной |
|
|||||
геометрии, когда контакты нанесены на поверхность исследуемого |
|
|||||
слоя структуры и, следовательно, внешнее напряжение приложено |
|
|||||
вдоль плоскости слоя. Схема поперечного транспорта при иссле- |
|
|||||
довании |
|
фотопроводимости |
квантово- |
-раз |
||
мерных структур не применяется из-за низкой фоточувствительности и отсутствия эффекта фотоэлектрического усиления.
60
В тех случаях, когда по каким-то причинам нельзя наносить верхний электрод и на поверхности слоя отсутствует хорошо выраженный барьер Шоттки илиp-n-переход, можно использовать электролитическую ячейку. Подбором электролита обычно удается создать на поверхности необходимый барьер. Недостатком этого способа является сложность электрохимических процессов, протекающих на границе полупроводника с электролитом и приводящих к необратимым изменениям образца в процессе измерений.
На рис. 2.15 показана схема измерительного конденсатора |
|
|||||||||
для измерения спектров конденсаторной фото-ЭДС. Конденсатор |
|
|||||||||
образуется |
прижатием |
к |
одной |
или |
обеим |
сторонам- |
|
|||
разца через тонкую пластинку слюды полупрозрачного электрода. |
|
|||||||||
Обычно |
|
|
полупрозрачный |
слой |
металла |
на |
||||
непосредственно на слюду. Метод предъявляет некоторые требо- |
|
|||||||||
вания к RC-цепям. Для неискаженной передачи на вход измери- |
|
|||||||||
тельной системы величины и кинетики фото-ЭДС, возникающей |
|
|||||||||
на обкладках конденсатора, должны выполняться условия: |
|
|
||||||||
|
|
|
|
tф >> (2pf)–1 << RC, |
|
(2.45) |
|
|||
где f |
— частота |
модуляции |
света; С — емкость |
измерительного |
|
|||||
конденсатора; R — сопротивление в цепи конденсатора; |
t — |
|
||||||||
характеристическое время релаксации фото-ЭДС. |
|
|
|
|||||||
Первое неравенство означает, что RC-цепочка должна быть |
|
|||||||||
интегрирующей. |
Поскольку |
|
емкость |
измерительного |
конден- |
|
||||
сатора |
невелика (~5 пФ), |
а |
частоты модуляции |
находятся |
|
|||||
в интервале 0,1–1 кГц, сопротивление R должно быть больше 108– |
|
|||||||||
109 Ом, что требует специального предусилителя. |
|
|
|
|||||||
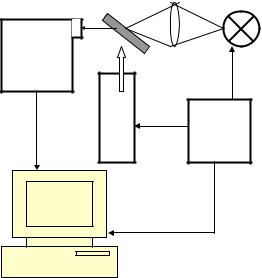
Структурная схема установки представлена на рис. 2.16. |
|
|||||||||
Источником монохроматического излучения служат галоген- |
|
|||||||||
ная |
лампа |
мощностью100 |
Вт и |
монохроматор с |
дифрак- |
|
||||
ционной решеткой. Интенсивность излучения на выходе монохроматора может изменяться при помощи нейтральных фильтров. Для согласования сопротивления образца с селективным усилителем применяется предварительный усилитель.
61
|
а |
б |
в |
|
|
|
г |
hn |
|
|
|
1 |
2 |
3 |
4 |
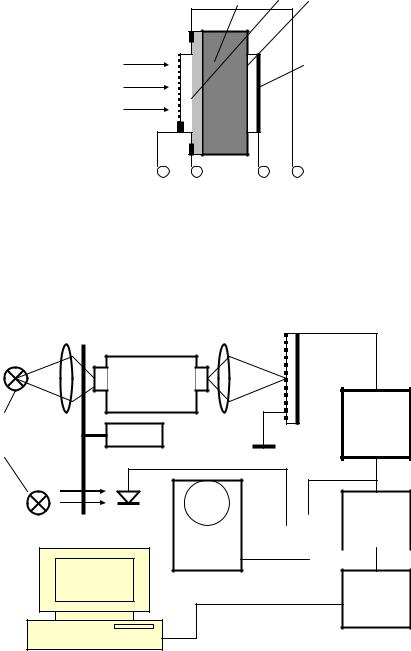
Рис. 2.15. Схема образца для измерения конденсаторной фото-ЭДС: а — исследуемая квантово-размерная структура; б — подложка; в — диэлектрик; г — электроды
4
2
5
1
3


 6 8
6 8 

9
7
Рис. 2.16. Структурная схема установки для измерения конденсаторной фото-ЭДС: 1 — лампы; 2 — монохроматор; 3 — модулятор; 4 — образец; 5 — селективный усилитель; 6 — синхронный детектор; 7 — цифровой вольтметр;
8 — осциллограф; 9 — компьютер
Регистрация сигнала производится синхронным детектором. Полученный спектр записывается с помощью компьютера. Для измерения спектров при высоких и низких температурах используют термостат и криостат.
2.5. Люминесцентные методы анализа
62
Люминесценция возникает в результате квантовых переходов атомов, ионов, молекул из возбужденных состояний в основное или менее возбужденное состояние. Эти атомы, ионы, молекулы принято называть центрами люминесценции, или, иначе, люминесцентными частицами. Элементарный процесс люминесценции имеет два этапа. На первом происходит возбуждение центра люминесценции, на втором — его высвечивание при переходе из возбужденного состояния в основное или менее возбужденное. Энергия рождающегося на заключительном этапе фотона
равна |
|
|
|
разности |
|
энергий- |
|
яний, |
между |
которыми |
произошел |
соответствующий - |
кван |
||
товый |
переход. |
Таким |
образом, центр |
люминесценции |
|||
использует энергию |
возбуждения, преобразуя ее |
в энергию соб- |
|
||||
ственного излучения. В этом смысле каждый центр люминесценции может рассматриваться как самостоятельный источник света. Исходя из вышесказанного, следует, что исследование параметров люминесцентного излучения позволяет получить информацию о виде и концентрации центров. Пути поступления энергии возбуждения к центрам люминесценции могут быть различными.
Это предопределяет разнообразие физических механизмов элементарных процессов люминесценции и длительность этих процессов.
Существуют различные способы возбуждения люминофоров.
В соответствии |
с этимиспособами различают несколько |
видов |
||
люминесценции. |
|
|
|
|
Фотолюминесценция — люминесценция, возникающая при |
||||
возбуждении |
светом |
видимого |
и |
ультрафиолет |
диапазонов частот (фотовозбуждение). На практике фотовозбуж- |
||||
дение используется для получения люминесценции жидких рас- |
||||
творов, стекол, |
твердых диэлектриков и |
полупроводников. При |
||
этом роль центров люминесценции играют специально вводимые в основное вещество ионы или молекулы. Так, например, в твердые диэлектрики и стекла вводят в виденебольших примесей ионы неодима (Nd3+) и других редкоземельных элементов. В жидкие растворители вводят, в частности, молекулы органических красителей.
Рассмотрим процессы, происходящие в центрах люминес-
ценции. |
Это могут |
быть атомы или молекулы, примесные |
ионы в |
твердом теле. В |
последнем случае речь идет об ионах |
с недостроенными внутренними электронными оболочками, например 3d- или 4d-оболочками (переходные металлы), 4f-оболочкой (редкоземельные элементы). Электроны этих оболочек как бы«экранированы» внешними заполненными оболоч-
63
ками от кристаллической решетки. Поэтому указанные электроны характеризуются определенными энергетическими уровнями, обусловливающими систему узких спектральных линий.
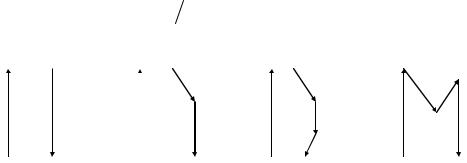
На рис. 2.17,а показаны квантовые переходы центра люминесценции, отвечающие наиболее простому физическому механизму люминесценции. При возбуждении центр переходит с уров-
ня Е1 на уровень Е2, а при обратном переходе рождается фотон |
|||||||||||||
(возникает люминесцентное свечение). Частота излучения люми- |
|||||||||||||
несценции соответствует разности энергий возбуждения и основ- |
|||||||||||||
ного уровня: w = (E |
2 |
- E ) h. Это есть резонансная люминесцен- |
|||||||||||
ция. |
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Е2 |
|
|
|
|
|
Е2 |
|
|
Е2 |
|
|
|
Е3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Е3 |
|
|
|
|
|
|
|
Е1 |
|
|
|
|
|
|
|
Е4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Е1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Е1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а |
|
|
б |
|
в |
|
|
г |
||||
Рис. 2.17. Простейшие механизмы люминесценции
Рис. 2.17,б иллюстрирует другой механизм люминесценции.
При возбуждении центр люминесценции совершает переход Е1®Е2. Затем он безизлучательно переходит на уровень Е3, передавая энергию другим частицам или расходуя ее на рождение
фононов. Испускание света происходит на переходеЕ3®Е1 |
и но- |
|||
сит название спонтанная |
люминесценция (название не вполне |
|||
удачное, поскольку любая люминесценция связана со спонтанным |
||||
испусканием света). |
|
|
|
|
Применяя |
к |
фотолюминесценции |
схему |
переходов |
(рис. 2.17,б), заключаем, что частота wл люминесцентного свечения меньше частоты поглощенного света. Рассматриваемая схема объясняет установленное в1852 г. правило Стокса, согласно
которому максимум спектра люминесценции сдвинут в сторону длинных волн по отношению к максимуму спектра поглощения. Расстояние между максимумами спектра поглощения и спектра люминесценции называют Стоксовым смещением. На рис. 2.17 показаны и другие возможные схемы переходов. Фотолюминесценция свойственна всем полупроводникам и диэлектрикам. Однако эффективность фотолюминесценции (характеризуемая квантовым или энергетическим выходом) существенно различается для разных материалов. Квантовый выход определяется отношением числа квантов люминесценции, излученных веществом, к числу поглощенных квантов возбуждающего света. Зависимость квантового выхода от интенсивности возбуждения может быть ли-
64
нейной, сублинейной (выход падает с увеличением интенсивности)
и |
сверхлинейной (выход |
растет |
с |
увеличением |
интенсив- |
|
ности). |
|
|
|
|
|
|
|
Катодолюминесценция — люминесценция при возбуждении |
|||||
образца |
электронным |
|
. пучкомКатодолюминесценция |
|||
возбуждается уже при энергиях электронов, в 1,5 раза превы- |
||||||
шающих |
ионизационный потенциал |
атомов. |
Однако для |
получе- |
||
ния достаточной для надежной регистрации интенсивности излучения обычно применяют пучки электронов с энергией выше100 эВ. Электроны таких энергий преодолевают потенциальный барьер, связанный с поверхностным зарядом кристалла, и выбивают вторичные , электроны которые, в свою очередь, ионизируют другие атомы кристаллической решетки. Этот процесс продолжается до тех пор, пока энергия вырываемых электронов достаточна для ионизации атомов. Образовавшиеся в результате ионизации дырки мигрируют по решетке и могут передаваться центрам люминесценции. При рекомбинации на этих центрах дырок и электронов возникает катодолюминесценция. Спектр катодолюминесценции аналогичен спектру фотолюминесценции. Ее КПД обычно составляет1–10 % от энергии электронного пучка. Катодолюминесценция широко применяется в вакуумной электронике (свечение экранов телевизоров, осциллографов, различных электрон- но-оптических преобразователей) и в качестве метода исследования структуры и свойств твердых веществ (рис. 2.18).
4 |
1 |
5 |
2
3
6
6
Рис. 2.18. Функциональная схема установки фото- и катодолюминесценции:
65

1 — исследуемый образец; 2 — ускоритель электронов; 3 — блок питания лампы и ускорителя;
4 — монохроматор; 5 — лампа (лазер); 6 — компьютер
Возбуждающие электроны имеют много большую энергию, чем фотоны, и потому пригодны для возбуждения широкозонных полупроводников. Наиболее высокоэнергичные электроны, использование которых еще не приводит к образованию радиационных дефектов, имеют кинетическую энергию около200 кэВ. Если не принимать во внимание радиационные дефекты, то катодолюминесценцию можно изучать при ещё больших энергиях. Электронный пучок позволяет легко осуществлять отклонение, фокусировку, модуляцию или работу в импульсном режиме.
Одним из недостатков возбуждения электронным пучком является то, что распределение плотности электронов в пучке гауссово.
Частично разрешить эту задачу можно с помощью диафрагмы, пропускающей электроны только вблизи максимума распределения. Другим недостатком является большой уровень потерь. Часто для исследования катодолюминесценции используют сканирующий электронный микроскоп, который позволяет зондиро-
°
вать полупроводник пучком с диаметром около 200 A .
Если осуществляется растровое или линейное сканирование электронного пучка (по всей поверхности образца или его части), то можно получить несколько типов отображений:
1)картину распределения катодолюминесценции;
2)картину морфологии, получаемую путем регистрации электронным коллектором отраженных и вторичных электронов;
3)картину наведенной электронным лучом проводимости;
4)если имеется приставка рентгеновского микрозондового анализа, то и химический состав облученной области.
Зная энергию ионизации и распределение потерь энергии, можно определить скорость генерации пар. Таким образом, кон-
центрация электронно-дырочных пар Np приближенно описывается выражением
N p = (J e)(E p E0 )(t d ), |
(2.46) |
где J — плотность тока в электронном пучке; Ep/E0 — число пар, генерируемых одним падающим электроном; t — время жизни электронно-дырочной пары; d — эффективная глубина проникновения первичных электронов.
Поскольку в результате рекомбинации электронно-дыроч- ной пары излучается фотон с энергиейhn » DΕg, эффективность преобразования в случае катодолюминесценции есть
66
h = |
|
DEg |
. |
(2.47) |
|
|
2, 8DEg + E1 |
|
|||||
В случае арсенида галлия h может достигать 30 %. |
|
|
|
|||
Электролюминесценция — люминесценция, возбуждаемая |
|
|||||
электрическим полем. Возбуждение центров люминесценции про- |
|
|||||
исходит в данном случае в результате возникновения в образце |
|
|||||
электрического разряда. В качестве примера отметим свечение |
|
|||||
газового разряда в газоразрядных трубках, а также свечение слоя |
|
|||||
твердого люминофора, находящегося между двумя параллель- |
|
|||||
ными |
|
|
|
, |
п |
|
к которым приложено электрическое напряжение. Свечение твер- |
|
|||||
дых веществ в электрическом поле впервые наблюдал О.В. Лосев |
|
|||||
в 1923 г. на карбиде кремния (SiC). |
|
|
|
|
||
Радиолюминесценция — люминесценция, возбуждаемая про- |
|
|||||
дуктами радиоактивного распада(a-частицами, быстрыми элек- |
|
|||||
тронами, g-квантами), а |
также |
различными |
ядерными |
|||
излучениями, например пучками нейтронов или протонов. Като- |
|
|||||
долюминесценция может рассматриваться как частный случай |
|
|||||
радиолюминесценции. |
|
|
|
|
|
|
Хемилюминесценция — люминесценция, сопровождающая |
|
|||||
химические реакции. Она возникает в тех случаях, когда один из |
|
|||||
реагентов оказывается в возбужденном состоянии. Частным слу- |
|
|||||
чаем хемилюминесценции является биолюминесценция(свече- |
|
|||||
ние гниющего дерева, некоторых насекомых, морских животных и |
|
|||||
др.); она связана с реакциями окисления особого вещества бел- |
|
|||||
кового происхождения, выделяемого светящимися организмами. |
|
|||||
Триболюминесценция — люминесценция, наблюдаемая |
при |
|
||||
растирании, раздавливании или раскалывании кристаллов. Во |
|
|||||
многих случаях триболюминесценция представляет собой фото- |
|
|||||
люминесценцию, возбуждаемую ультрафиолетовым излучением |
|
|||||
разряда, который возникает в местах разлома кристалла, у тру- |
|
|||||
щихся поверхностей. |
|
|
|
|
|
|
Термолюминесценция — люминесценция, возникающая |
при |
|
||||
нагревании вещества, предварительно возбужденного светом или |
|
|||||
рентгеновским излучением. Механизм |
термолюминесценции — |
|
||||
рекомбинационный. Когда кристалл возбуждается оптически или |
|
|||||
электронным пучком, может происходить заполнение глубоких |
|
|||||
уровней. Те носители, которые были захвачены глубокими уров- |
|
|||||
нями, остаются на ловушках после |
прекращения |
возбуждения. |
|
|||
При |
|
нагревании |
|
, |
|
|
захваченные ловушками, освобождаются и происходит излучательная рекомбинация их с ионизированными при возбуждении центрами люминесценции. Когда носители освобождаются из ло-
67
вушек, они могут принять участие в измеримых процессах, таких как дрейф в электрическом поле (термостимулированный ток) или накопление заряда на поверхности(термостимулированная емкость).
Обычно твердое тело имеет не один, а несколько уровней ловушек; они находятся на разных расстояниях от дна зоны проводимости. По мере нагревания кристалла сначала будут освобождаться электроны из ловушек вблизи дна зоны проводимости, а затем уже из более глубоко расположенных ловушек. В результате интенсивность термолюминесценции будет изменяться по мере увеличения температуры . На кривой термовысвечивания, отражающей зависимость интенсивности от температуры, обнаруживается ряд максимумов, каждый из которых соответствует определенной группе ловушек.
Вероятность освобождения электрона из ловушки в единицу
времени определяется выражением |
|
P = s exp(–Et/kT). |
(2.48) |
Величину s можно записать в виде |
|
s = Nbvtst, |
(2.49) |
где Nb — плотность состояний в зоне, в которую переходят носители; vt — тепловая скорость носителей; st — сечение захвата носителей ловушкой.
Если nt — концентрация захваченных ловушками электронов, то скорость её изменения вследствие теплового возбуждения оп-
ределяется как |
|
dnt/dt = –ntP. |
(2.50) |
Если освобожденные электроны вновь не захватываются ло- |
|
вушками, то решение этого уравнения имеет вид |
|
nt = nt0exp(–t/t), |
(2.51) |
где nt0 — начальная концентрация захваченных электронов.
Если излучательное время жизни tr много меньше, чем время освобождения электронов t, то интенсивность света будет меняться со скоростьюh(dnt/dt) (h — эффективность излучательной рекомбинации). Тогда интенсивность термолюминесценции может быть определена из уравнения
L(t,T) = (nt0hs)exp(–t/t)exp(–Et/kT). (2.52)
Из уравнения (2.52) следует, что для определения энергетического положения уровня ловушки могут быть использованы два экспериментальных метода: 1) измерение времени спада люми-
несценции при различных фиксированных температурах; 2) |
изме- |
рение температурной зависимости термолюминесценции в раз- |
|
личные моменты времени. Отметим, что эти два |
метода |
68
эквивалентны, так как в обоих случаях необходимо определениеt и Т. Температурная зависимость эффективности излучательной рекомбинации может быть установлена с помощью другого эксперимента, в частности путем измерения эффективности при стационарном режиме возбуждения.
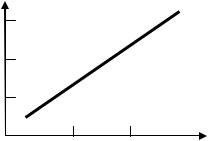
На рис. 2.19 в качестве примера дана температурная зависимость постоянной времени спада термолюминесценции, которая описывается соотношением
t = (1/s)exp(Et/kT). |
(2.53) |
Из наклона прямой можно определить глубину ловушкиEt, которая для рассмотренного здесь случая(ZnS, легированный Сu) оказывается равной 1,0 эВ. По-видимому, это значение можно рассматривать как энергию, необходимую для возбуждения электрона из валентной зоны на акцепторный уровень Сu. В результате становится возможной излучательная рекомбинация электрона
зоны проводимости с в валентной зоне. Следовательно, примесь Сu работает как дырочная ловушка.
lgt 4
3
2
1
2,2 2,3 2,4 1/T,10-3K-1
Рис. 2.19. Логарифм времени спада термолюминесценции в зависимости от температуры для ZnS
Вторым методом определения характеристик термолюминесценции является увеличение температуры образца с постоянной
скоростью. С ростом температуры в первую очер освобождаются мелкие ловушки. Если имеется только один уровень захвата, интенсивность термолюминесценции проходит через максимум и затем уменьшается по мере истощения ловушек.
Чем меньше скорость нагрева, тем более четко выявляется структура кривой высвечивания (рис. 2.20).
69

L ,
отн. ед.
6
3
0 
100 150 200 T , K
Рис. 2.20. Кривая термовысвечивания для ZnS
70
3. РЕНТГЕНОВСКИЙ АНАЛИЗ 3.1. Общие сведения о рентгеновском излучении
Рентгеновские лучи представляют собой электромагнитные колебания, длина волны которых (10–7–1014 м) сравнима с линейными размерами атомов. Открытие рентгеновских лучей принадлежит В. Рентгену (1895), а их волновая природа была установлена спустя 17 лет М. Лауэ совместно с В. Фридрихом и П. Книппингом, которые обнаружили дифракцию (рассеяние) рентгеновских лучей на кристаллах. Эти невидимые лучи способны вызывать флуоресценцию кристаллических веществ (цинковая обманка, барий платиносинеродистый и др.), воздействовать на фотопластинки (засвечивать их через непрозрачные для видимого света экраны) и ионизировать газы. Данные явления используются для обнаружения и диагностики рентгеновских лучей, а также широко применяются в практике. Известны два типа рентгеновского излучения: тормозное и характеристическое.
Тормозное излучение возникает в вакууме, когда быстролетящие электроны тормозятся при падении на анод рентгеновской
трубки, т.е. уменьшение |
скорости |
электронов |
v1 от |
|
до v2 при торможении является источником излучения: |
|
|||
|
m (v12 - v22 ) |
|
|
|
hn = |
|
. |
|
(3.1) |
2 |
|
|||
|
|
|
|
|
Скорости электронов, необходимые для возникновения рентгеновских лучей, должны быть сопоставимы со скоростью света. Для достижения таких скоростей электроны разгоняются в полях с разностью потенциалов порядка 108 В. Поскольку переход от v1 к
v2 |
монотонен, |
тормозное |
излучение разлагается |
в сплошной |
спектр, |
имеющий |
резкую |
||
в |
коротковолновой части, соответствующей скорости |
электрона |
||
v2 = 0.
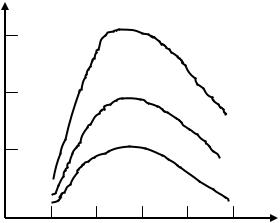
Вид зависимости интенсивности сплошного спектра торможения при одном и том же направлении, но для различных материалов (металлов) анода приведен на рис. 3.1. Как видно из рис. 3.1, положение коротковолновой границы не от природы тормозящего слоя(т.е. атомного номера металла
антикатода), а от кинетической энергии и массы быстролетящей заряженной частицы (электрона).
71
I,
отн. ед. 3
2
Z=47 1 Z=29
Z=13
1,2 1,6 2,0 2,4 2,8 l, нм
Рис. 3.1. Вид зависимости непрерывного спектра торможения
Характеристические рентгеновские лучи возникают при переходе электрона с более удаленной от ядра орбитали атома на более близкую в том случае, если на этой орбитали образовалась вакансия. Характеристические рентгеновские лучи обладают линейчатым спектром, подобным оптическим спектрам газов.
Однако структура характеристических спектров рентгеновских лучей (число линий, их относительное расположение и яркость) не зависит от природы излучающего вещества, ею определяется только положение спектра на шкале частот, который смещается в сторону коротких волн с увеличением порядкового номера элемента.
Закон, связывающий частоту спектральных рентгеновских линий характеристического излучения с порядковым номером эле-
ментов (Z), был |
открыт . МозлиГ |
в 1913 |
г. |
и формулируется следующим образом: квадратный |
корень |
из |
|
частот (n) соответствующих характеристических линий является линейной функцией порядкового номера элементов. Это означает, что если за счет энергии, поступившей извне (например, за счет мощной электронной бомбардировки), выбит электрон из
атома |
с |
самой |
|
близкой |
к |
ядру (n=1),орбитали |
|||||||
то |
на освободившееся |
место |
может |
перейти электрон 2-сой, |
|||||||||
3-й, 4-й |
и |
.т.дорбиталей, |
в |
результате |
чего |
получается |
|||||||
(высвечивается) |
квант |
рентгеновского |
|
¢ |
= hn2 |
, |
|||||||
излученияEK |
|||||||||||||
¢¢ |
= hn3, |
¢¢¢ |
|
Спектр |
|
полученного |
излучения |
|
назван |
||||
EK |
EK = hn4. |
|
|
||||||||||
K-серией. Если электрон выбит со второй орбиты(n=2), то пере- |
|||||||||||||
ходу электронов на этот уровень с более удаленных орбит будут |
|||||||||||||
отвечать |
кванты |
энергии |
рентгеновского |
|
¢ |
= hn |
|
, |
|||||
излученияE |
3 |
||||||||||||
¢¢ |
= hn4, |
¢¢¢ |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
EL |
EL = hn5 и т.д. Спектр такого излучения назван L-серией. |
||||||||||||
72
Переходу электронов с более высоких уровней на третью орбиту будет соответствовать M-серия и т.д.
Рентгеновские лучи, проходя через вещество, частично поглощаются. Соотношение между интенсивностью входящего потока I0 и проходящего через слой веществаI имеет вид (закон Бугера — Ламберта)
I/I0 = exp(–ml), |
(3.2) |
где m — коэффициент поглощения; l — толщина поглощающего слоя.
Для каждого элемента, входящего в состав поглощающего образца, величина m в зависимости от частотыn рентгеновского излучения изменяется скачками. Всплески на кривой поглощения соответствуют резонансному поглощению, вызванному перескоком электронов с уровнейn=1 (K-поглощение), n=2 (L- поглощение), n=3 (М-поглощение) и т.д. Характер этой зависимости, а именно крутое падение кривой с увеличением частоты( уменьшением длины волны А) и наличие всплесков, связанных с резонансным поглощением, выражено соотношением
m = (0,013/l)rZmλn, |
(3.3) |
где r — плотность вещества; Z — заряд ядер элементов; l — длина волны излучения; А — атомная масса элемента; m и n — величины, близкие к 3 и 4 соответственно и в небольшой степени обусловленные значениями l и Z.
Таким образом, на коэффициент поглощения рентгеновского излучения существенно влияют природа поглощающего вещества, его плотность и длина волны излучения.
3.2. Дифракция рентгеновских лучей
Анализ формулы (3.3) указывает, что m — чрезвычайно малая величина, это свидетельствует о слабом поглощении рентгеновских лучей веществом, их высокой проникающей способности. Эта особенность, а также дифракция рентгеновских лучей на кристаллических решетках служат основой их практического использования для изучения структуры оптически непрозрачных веществ без их разрушения. Для возникновения явления дифракции необходимо, чтобы расстояние между соседними плоскостями отражения в рассеивающем кристалле было не менее половины длины волны падающего луча. Длины волн видимого света находятся в интервале 400–700 нм, а межплоскостные расстояния в кристаллических ре-
шетках изменяются в пределах 1 нм. Вот почему для структурного
73
анализа используют рентгеновские лучи, длина волн которых 102–
103 нм.
Дифракция рентгеновских лучей наблюдается в газах, жидко- |
|
|||
стях и аморфных веществах, наиболее четко она проявляется на |
|
|||
кристаллах. |
На |
дифракции |
рентгеновских |
лучей |
кристаллами |
основаны |
разработанные |
рентгеноструктурный |
|
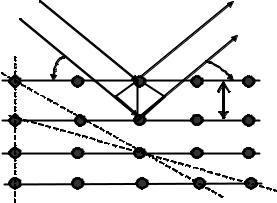
и рентгенофазовый методы анализа. Суть дифракции рентгеновских лучей заключается в сложении амплитуд вторичных волн, рассеянных электронами, образующими электронные оболочки атомов исследуемого вещества, без изменения частоты колебаний. Схематически дифракция рентгеновских лучей представлена на рис. 3.2.
q q
d si n q |
dsi n q |
d |
|
Рис. 3.2. Схема дифракции рантгеновских лучей (к выводу формулы Вульфа — Брега)
Число и характер пространственного распределения разрешенных направлений рассеяния (дифрагирование) рентгеновских лучей определяются законом Ю. Вульфа и У. Брегга (1913), который выражается соотношением
|
|
2d sinq = nl, |
|
(3.4) |
|
где d — расстояние между соседними отражающими плоскостями |
|
||||
в |
кристалле; |
q — угол |
скольжения, образованный |
|
|
направлением падающих на кристалл лучей с отражающейпо |
|
||||
верхностью; n — порядок отражения, в котором при заданных d и |
|
||||
q |
может |
наблюдаться |
|
дифракционный ; |
максиму |
l — длина волны рентгеновского излучения. |
|
|
|||
|
Если исследуемый кристалл, помещенный на пути монохро- |
|
|||
матического (l = const) рентгеновского луча, поворачивать вокруг |
|
||||
перпендикулярной к лучу оси и таким образом ставить поочеред- |
|
||||
но систему плоскостей кристалла в отражающее положение, то |
|
||||
наблюдается полная картина рассеяния. Дифракционную картину |
|
||||
можно получить и без вращения образца, используя источник с |
|
||||
непрерывным спектром рентгеновского излучения. В этом случае |
|
||||
для |
всех систем |
плоскостей кристалла в |
непрерывном спектре |
|
|
74

обязательно найдется длина волныl, удовлетворяющая закону Вульфа—Брегга.
Определив углы падения рентгеновских лучейq, при которых наблюдаются интерференционные максимумы, можно определить индексы плоскостей, ответственных за соответствующий максимум.
Для кубических кристаллов это выглядит так. Из формул
si n q = nl 2dhk l ; dhk2 |
l = a2 (h2 + k 2 + l 2 ), |
(3.5) |
где h, k, l — индексы Миллера для атомных плоскостей, получаем равенство
si n2 q = |
l2 |
é(nh)2 |
+ (nk )2 |
+ (nl )2 ù. |
(3.6) |
|
4a2 |
||||||
|
ë |
|
û |
|
Постоянный для данного кристалла коэффициентl2/4a2 позволяет, кроме того, определить параметр ячейкиа. Изучая интенсивности отражений на дифракционной картине, можно определить положение атомов в элементарной ячейке кристалла.
Зная dhkl, рассчитывают значения углов для соответствующей системы плоскостей. При этом для полупроводников со структурой алмаза учитывают, что отражения от некоторых плоскостей могут гаситься. Значения углов q для ряда материалов приведены в табл. 3.1.
Таблица 3.1 Углы отражения для основных кристаллографических
плоскостей важнейших полупроводниковых материалов,
|
|
° |
|
|
|
|
l = 1, 54 A |
|
|
||
Полупроводниковый |
Кристаллографические плоскости |
||||
материал |
|
|
|
|
|
(400) |
(220) |
(111) |
(224) |
||
|
|||||
Ge |
33°02¢ |
22°40¢ |
13°39¢ |
41°53¢ |
|
Si |
34°37¢ |
23°42¢ |
14°13¢ |
44°04¢ |
|
GaAs |
33°02¢ |
22°42¢ |
13°40¢ |
41°53¢ |
|
InSb |
28°13¢ |
19°42¢ |
11°55¢ |
35°39¢ |
|
Порядок отражения |
n=4 |
n=3 |
n=1 |
n=2 |
|
|
|
|
|
|
|
В производственной практике существует задача определения кристаллографических направлений, лежащих в плоскости торца слитка. В частности, представляет интерес определить одно из основных направлений системы [110] в плоскости (111) или (100) для последующего ориентирования пластины. Обычно ориентировку полупроводниковых монокристаллов проводят по методу Лауэ при
75
использовании немонохроматического излучения. Так как размеры монокристаллов и слитков достаточно велики, то используется съемка на отражение (метод эпиграмм).
Принцип метода заключается в следующем. При падении рентгеновского излучения на торец слитка отраженные лучи возникают только от тех систем плоскостейhkl, для которых выполняется условие Вульфа — Брэгга. Обычно используют отражение под большими угламиq, близкими к 90°. Отполированный торец слитка устанавливают нормально по отношению к падающему рентгеновскому излучению. Полученную эпиграмму анализируют с использованием стандартных сеток Вульфа, представляющих
собой номограмму стереографических проекций параллелей и
меридианов сферы. В результате анализа определяют два угла, |
|
||||||
на которые необходимо повернуть слиток вокруг оси, чтобы вы- |
|
||||||
вести искомую кристаллографическую плоскость и провести резку |
|
||||||
слитка. Используя метод Лауэ, проводят ориентацию слитков Ge и |
|
||||||
Si по плоскостям (100). Слитки GaAs ориентируют |
для |
резки по |
|
||||
плоскостям (111). Этот метод применяют и для ориентации слит- |
|
||||||
ков сапфира и других материалов. |
|
|
|
|
|
||
Источниками рентгеновского излучения служат рентгеновские |
|
||||||
трубки, представляющие собой двухэлектродные электровакуум- |
|
||||||
ные приборы. Для возбуждения в них рентгеновского излучения |
|||||||
создается поток свободных электронов высокой |
кинетической |
||||||
энергии, который направляется на металлическую мишень, где |
|
||||||
происходит взаимодействие быстрых электронов с веществом и |
|||||||
возникает рентгеновское излучение. Рентгеновская трубка имеет |
|
||||||
вид |
баллона, |
выполненного |
|
|
или |
|
целиком |
из стекла, или из стекла и металла. В баллоне расположены катод |
|
||||||
и анод. |
Катодом служит V-образная |
или |
спиральная нить |
из |
|||
вольфрама, нагреваемая |
до 2273–2973 К |
током |
низковольтного |
|
|||
трансформатора. Катод помещен в устройство, фокусирующее на |
|
||||||
анод поток электронов. Анодом служит плоский участок на внут- |
|
||||||
ренней стороне дна массивного медного цилиндра. На этот уча- |
|
||||||
сток, |
играющий |
роль |
|
мишени |
при- |
бо |
|
дировке электронами, наносят слой того или иного металла(пай- |
|
||||||
кой или гальваническим способом) для получения нужной длины |
|
||||||
волны характеристического излучения. |
|
|
|
|
|
||
Поскольку КПД трубки низок (1–3 %), почти вся потребляемая |
|
||||||
мощность при ее работе превращается в теплоту, для отвода ко- |
|
||||||
торой применяют систему охлаждения анода. Окна из тонкой бе- |
|
||||||
риллиевой фольги позволяют пропускать излучение от0,4 нм и |
|
||||||
менее. |
Для |
работы |
трубок |
|
подобного |
||
в них необходимо создавать разрежение в пределах от1 до 10–2 Па. Следует отметить, что существуют различные варианты рент-
76
геновских трубок, число которых достаточно велико, поскольку весьма широк диапазон областей применения рентгеновского излучения (медицина, дефектоскопия, структурные исследования и т.д.). Как уже отмечалось, явление дифракции рентгеновских лучей широко используют для изучения структуры и фазовогосо става веществ.
3.3. Рентгеноструктурный анализ
Для проведения рентгеноструктурного анализа исследуемый кристаллический образец помещают на пути рентгеновского луча с длиной волны от0,07 до 1 нм, который взаимодействует с кристаллом. В итоге получается дифракционная картина, регистрируемая или с помощью фотоэмульсии, или специальным электронным детектором. Анализируя ее, находят пространственное расположение атомов в узлах кристаллической решетки, определяют размеры элементарных ячеек кристалла, число частиц в них и симметрию их расположения. При изучении дифракционного спектра кристалла используют уравнение Вульфа— Брегга (3.4). Разработано несколько методов рентгеноструктурного анализа.
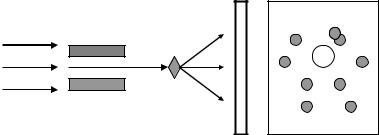
Метод Лауэ применяют для исследования структуры монокристаллов. Монокристаллический образец помещается на пути рентгеновского луча, обладающего сплошным спектром (рис. 3.3). Этот немонохроматический луч, падая на кристалл, взаимодействует с ним. В результате дифракции на фотопленке появляются темные пятна (см. рис. 3.3), расположенные в виде эллипсов, гипербол и прямых, проходящих через пятно от первичного пучка (незаштрихованный круг), что удовлетворяет условию Вульфа— Брегга.
1
5
2 3
4
Рис. 3.3. Схематическое изображение прибора, работающего по методу Лауэ, и дифракционной картины (лауэграмма): 1 — входящий поток рентгеновского излучения; 2 — коллиматор;
3 — образец; 4 — рассеянный луч; 5 — плоская фотопленка
77
При определенной ориентировке монокристалла полученная картина позволяет установить основные элементы симметрии кристалла, но не структурные характеристики (размер элементарной ячейки кристалла, число атомов в ней и т.д.).
В методе «порошка», или дебаеграмм, используют монохроматическое рентгеновское излучение. Поликристаллический образец помещают на пути узкого рентгеновского луча. Поскольку в порошке имеются кристаллы любой ориентации по отношению к
лучу, |
всегда |
найдутся |
такие |
, |
крист |
|
положение |
которых |
отвечает |
условию |
Вульфа— Брегга. |
|
|
В конечном итоге все те кристаллические частицы в порошке, ко- |
|
|||||
торые имеют |
соответствующие межплоскостные |
расстояния |
||||
d1, d2, d3, ..., dn, |
попадают |
по |
отношению |
к падающему |
лучу |
|
в «отражающее» (но не гасящее) положение. Отраженные лучи |
|
|||||
образуют конус со строго определенным углом расхождения. |
|
|
||||
При съемке рентгенограммы в методе«порошка» полоску |
|
|||||
фотопленки размещают вокруг образца(в кассете) так, чтобы |
|
|||||
входящий рентгеновский луч пересекал ее по диаметру. В резуль- |
|
|||||
тате каждый конус отраженных лучей оставит на фотопленке за- |
|
|||||
свеченный |
след |
в |
виде , симметричнодужек |
рас- |
||
положенных |
относительно |
направления |
первичного . |
луча |
||
Определив расстояние между дужками и радиус кольца фотопленки, можно вычислить углы расхождения конусов отраженных лучей и угол их падения на отражающую плоскость кристаллов ,и следовательно, длину волны монохроматического рентгеновского излучения l, а также значения межплоскостных расстоянийd в кристалле.
Без дополнительных сведений о симметрии кристаллов -ис следуемого вещества дальнейшая расшифровка структуры по данным метода «порошка» невозможна. Однако простота эксперимента и расчета межплоскостных расстояний объясняет достаточно широкое распространение этого метода в рентгенофазовом анализе.
Более полную информацию о структуре кристаллов можно получить, пользуясь методом вращения. Суть его состоит в том, что монокристалл, помещенный на пути монохроматического рентгеновского луча, равномерно вращается вокруг оси, совпадающей с одним из наиболее важных кристаллографических на-
правлений |
в |
, кристалле |
перпендикулярно |
к направлению |
луча(рис. 3.4). |
Переменным |
параметром здесь |
является угол q. Съемка рентгенограммы производится на широкую фотопленку, находящуюся в цилиндрической кассете. Лучи отражения, возникающие при определенных углахq, распространяются по образующим конусов и при пересечении с фотопленкой
78
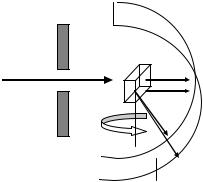
оставляют на ней линии пятен, которые называют слоевыми (рис. 3.4). По расстояниям между слоевыми линиями рассчитывают период решетки кристалла в направлении его оси вращения. Однако этот метод не позволяет соотнести местоположение каждого пятна с углом q, что достигается методами вращения-качания и рентгеногониометра.
4
1 3
2
Рис. 3.4. Схема съёмки рентгенограммы методом вращения: 1 — рентгеновское излучение; 2 — диафрагма; 3 — вращающийся монокристалл;
4 — фотопленка
Метод качания заключается в , томчто монокристалл не делает полных оборотов вокруг выбранной оси, а совершает лишь небольшие качания в узких угловых промежутках. Координаты угловых промежутков строго измеряют и определяют величину q, характеризующую соответствующее дифракционное пятно.
В одном из методов рентгеногониометра— методе Вайссенберга — вращение образца сохраняется, но внутренним экраном «вырезается» только один конус отраженных лучей. Одновременно с вращением монокристалла производится осевое движение фотопленки так, что дифракционная картина одного слоя разворачивается на всю площадь
и каждому пятну отвечает известный уголq (см. рис. 3.4). При обработке такой вайссенбергограммы соотносят ориентацию -кри сталла с местоположением пятна, что создает условия для проведения количественных расчетов структурных характеристик.
Для этого необходимо иметь правильно сформированный
монокристалл малого размера (в долях миллиметра). Предвари- |
|
||||||
тельно |
методами |
Лауэ |
или |
рентгеногониометра - |
устана |
||
ливают |
симметрию |
кристаллической |
решетки |
и |
по- |
распо |
|
ложению дифракционных пятен вычисляют парамет элементарной ячейки кристалла. Затем определяют интенсив-
ность потемнения I дифракционных пятен и путем обработки этих
79

данных находят так называемые структурные факторыF2, а отсюда абсолютное значение структурной амплитуды F:
F (hk l ) = |
å |
f |
i |
exp é2pi (hx |
i |
+ k y |
i |
+ l z |
)ù, |
(3.7) |
|
|
ë |
|
i |
û |
|
где xi, yi, zi — коэффициенты i-гo атома; h, k, l —индексы отражающей плоскости; fi — атомный фактор, который представляет собой функцию, дающую значение амплитуды когерентного рассеяния рентгеновских лучей изолированным атомом или ионом.
Интегральную формулу структурной амплитудыF(hkl) выражают через электронную плотность
F (hk l ) = ò r(x y z) ex p 2pi (hx + k y + l z)dV , |
|
(3.8) |
|||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
откуда с помощью преобразований получают |
|
|
|
|
|
|
|||||
|
1 |
¥ |
|
|
ë |
i |
|
i |
i |
û |
|
|
ååå |
|
|
|
|||||||
r(x y z) = |
|
|
F (hk l ) exp |
é2pi (hx |
|
+ k y |
|
+ l z |
)ù, |
(3.9) |
|
|
|
|
|
|
|||||||
V0 h k |
l |
|
|
|
|
|
|
|
|
||
где V0 — объем элементарной ячейки. |
|
|
распределение |
элек- |
|||||||
Из выражения (3.7) |
можно вычислить |
|
|||||||||
тронной плотности в атомах и координаты их в ячейке кристалла. Полученные значения наносят на график, и точки равной плотности r(xyz) соединяют непрерывными линиями. В результате получают картину, подобную изображению рельефа местности на топографической карте, где пользуются изолиниями.
На рис. 3.5 приведена проекция распределения электронной плотности для кристалла RhSb2. Эти данные получены при рентгеноструктурном анализе молекулярного кристалла указанного соединения. Из рис. 3.5 четко видна локализация атомов сурьмы относительно атома родия, что позволяет с большой точностью определить параметры кристаллической решетки этого соединения.
Метод рентгеноструктурного анализа имеет свои особенности |
|||||||||
и ограничения, он трудоемок, требует получения монокристаллов, |
|||||||||
|
часто не позволяет с высокой |
точно- |
|||||||
|
стью |
определить |
длины |
связей |
и - ва |
||||
Sb |
лентные |
углы, расчет |
структуры |
кри- |
|||||
|
сталлов даже с применением ЭВМ |
||||||||
Rh |
длителен. |
|
|
Все |
|
|
это |
||
не умаляет |
очевидных |
достоинств |
ме- |
||||||
|
тода, области его применения обшир- |
||||||||
Sb |
ны. Знание структуры и энергетики |
со- |
|||||||
Рис. 3.5. Распределение |
единений дает возможность установить |
||||||||
характер |
и |
прочность |
химических |
свя- |
|||||
электронной плотности |
зей, уточнить формулу, найти плотность |
||||||||
в кристалле RhSb2 |
|||||||||
и выявить новые химические соедине- |
|||||||||
|
|||||||||
|
|
80 |
|
|
|
|
|
|
|
ния в системах взаимодействующих веществ.
Наиболее четкие рентгенограммы наблюдаются для кристаллических образцов, а жидкости, стекла и аморфные вещества характеризуются наличием лишь размытых дифракционных колец, интенсивность которых резко падает с увеличением угла падения. Тем не менее, анализируя такие дифрактограммы, можно получить обширную информацию о строении этих сред, в которых отсутствует дальний порядок(т.е. упорядоченное расположение частиц вдали от атома или молекулы, выбранной условным центром), но имеет место ближний порядок со свойственным ему упорядоченным расположением частиц, находящихся в непосредственной близости от условного центра. Особое значение рентгеноструктурный анализ приобрел при изучении металлов и их сплавов (кристаллохимия сплавов). Однако применение рентгеновских лучей не ограничивается только определением структур. Известны и другие варианты использования явления дифракции — рентгенофазовый анализ и рентгеновская микроскопия.
3.4. Рентгенофазовый анализ
Рентгенофазовый анализ представляет собой метод качественного или количественного определения числа и соотношений кристаллических фаз в системах различной сложности. Он основан на том, что каждая кристаллическая фаза дает индивидуальную, неповторимую картину расположения дифракционных колец и их интенсивностей. Поэтому при изучении смеси кристаллов различных веществ дифракционная картина будет представлять сумму их дифрактограмм, интенсивность которых пропорциональна количественному содержанию каждого из них в смеси. Для идентификации кристаллических форм(фаз) необходимо снять дифрактограммы эталонных кристаллических образцов или воспользоваться специальными таблицами(картотекой), содержащими сведения о межплоскостных расстояниях и относительных интенсивностях линий рентгенограмм огромного числа кристаллических веществ.
Дифракционная картина в рентгенофазовом анализе обычно регистрируется в условиях метода«порошка» дифрактометрически с помощью счетчиков рентгеновских квантов.
Метод рентгенофазового анализа применяют при исследовании свойств сложных систем с различными видами взаимодействий (плавление, растворение, образование и распад химических соединений).
Рентгенофазовый анализ позволяет определять содержание каждой из фаз с точностью до 1 %. В некоторых комбинациях кристаллических фаз уровень чувствительности понижается до 10 %.
81
В целом метод универсален, прост, дает однозначную информа-
цию |
и |
потому |
широко |
в практике. |
|
|
|
Определение |
фазового |
состава исследуемого |
кристалличе- |
ского вещества проводят методом сравнения найденных по экс-
периментальным |
данным |
межплоскостных |
расстоянийd |
и интенсивностей |
соответствующих линий рентгенограммыI |
||
с табличными данными этих величин, сведенных в справочникиопределители. При их совпадении делают вывод о правильном определении вещества и его кристаллической модификации. Однако из-за ошибок эксперимента и специфики исследуемых - ве ществ полученные результаты могут отличаться от приведенных в справочниках, что чаще всего наблюдается при определенииI.
При этом чем большеq, тем угол более точно совпадают экспериментальные и табличные значе-
ния d.
При определении фазового состава образца на его рентгенограмме выделяют три наиболее интенсивные линии, выписывают межплоскостные расстояния и сравнивают их с аналогичными значениями d и I ключа-определителя. После этого для контроля весь набор экспериментальных межплоскостных расстояний и соответствующих интенсивностей сравнивают с табличными значениями соответствующих веществ и их модификаций.
Расчет рентгенограммы исследуемого образца производят следующим образом:
1)нумеруют линии, начиная от центра рентгенограммы;
2)определяют интенсивность линий по десятибалльной шка-
ле; |
|
|
|
|
3) |
измеряют |
расстояние |
между симметричными |
линиями |
спектра и, введя поправку на поглощение в образце, находят ве- |
||||
личину 2l; |
|
|
|
|
4) |
по углам q |
находят sinq |
и сравниваютsinq всех |
линий |
с sinq наиболее интенсивной линии с целью отобрать и отбросить фиктивные значения d, связанные с немонохроматичностью рентгеновского излучения;
5) для нефиктивных линий вычисляют величиныd — межплоскостные расстояния, выбирают три наиболее интенсивные линии и по их d и I путем сравнения с данными ключаопределителя находят фазовый состав образца.
Рентгенофазовый анализ широко используют в металловедении (для изучения фазового состава металлов и сплавов), минералогии (для установления состава сложных минералов), химии и химической технологии.
82
5.5. Рентгеноспектральный анализ
Для получения спектра рентгеновских лучей в рентгеноспектральном анализе используют их дифракцию на кристаллах (или на штриховых дифракционных решетках) при таких малых углах q (1–12°), что рентгеновские лучи испытывают отражения, как бы скользя по поверхности отражающего кристалла. Угол q, образованный падающим или лучом и поверхностью кристалла(или дифракционной решетки), назван углом скольжения. Отраженные лучи, как и рассеянные, дифрагируют на структуре отражающей поверхности, и получившаяся дифракционная картина подчиняется закону Вульфа— Брегга (см. (3.4)).
Исследуемый образец при рентгеноспектральном анализе облучается первичными рентгеновскими лучами. Атомы элементов, входящих в состав образца, под действием излучения возбуждаются и сами становятся источниками вторичного рентгеновского излучения. Такой способ возбуждения получил название флуоресцентного.
Специфический для данного вещества спектр вторичного излучения описывается как корень квадратный из частот колебаний лучей, испущенных атомами, входящими в состав образца, и линейно зависит от их атомных номеров:
n = Ra(Z - s), |
(3.10) |
где n — частота колебаний, связанная с длиной волны соотношением n = c/l; R — постоянная Ридберга; а — постоянная для каждой линии спектра величина; Z — атомный номер элемента; s — средняя константа экранирования, в небольших пределах зависящая от Z.
Из уравнения (3.10) следует, что каждому виду атомов свойственна определенная частота колебаний вторичных рентгеновских лучей, возбужденных первичным излучением. Очевидно, что энергия кванта возбуждения должна быть больше энергии, необходимой для выбивания глубинных электронов атомов исследуемого вещества, т.е. флуоресцентное излучение исследуемого образца получается в тысячи раз слабее первичного излучения, что затрудняет регистрацию спектров.
На рис. 3.6 приведена принципиальная схема рентгеновского спектрометра с изогнутым кристаллом, где первичные рентгеновские лучи из источника падают на исследуемый образец, вызывая вторичное флуоресцентное излучение. Часть излучения через диафрагму подается под малым углом на поверхность изогнутого кристалла и под углом
83
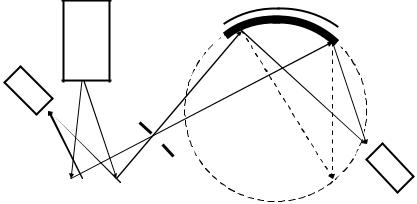
отражается |
от |
него. Поскольку |
этот |
угол |
в |
соответствии |
суравнением Вульфа — Брегга должен быть различным для компонентов излучения с разными длинами волнl, отраженные от изогнутого кристалла лучи, будучи сфокусированными на кольцевой экран (пунктирная окружность), образуют на нем спектр. Этот спектр может быть зафиксирован фотографическим способом или
спомощью электронного детектора.
3 |
5 |
|
|
1 |
|
|
4 |
|
2 |
6 |
|
Рис. 3.6. Блок-схема рентгеновского спектрометра
сизогнутым кристаллом:
1— дополнительный электронный спектрометр; 2 — образец; 3 — рентгеновская трубка;
4 — диафрагма; 5 — изогнутый отражающий кристалл; 6 — электронный детектор
Используемые в рентгеноспектральном приборе отражающие кристаллы достаточно разнообразны по природе и обычно представляют собой кристаллы фтористого лития, гипса, кварца, слюды и др. В области длин волн1,5–50 нм их можно заменить искусственно изготовленными дифракционными решетками, которые могут работать при малых углах скольжения в1–12°. В качестве детекторов излучения в зависимости от области спектров используют счетчики Гейгера и различные счетчики квантов.
Рентгеноспектральный анализ применяют для количественного определения содержащегося в пробах элемента, начиная с Mg (Z=12). При этом образцы (металлические сплавы, стекла, минералы, керамика, пластмассы и т.д.) имеют сложный фазовый и химический состав. Как правило, образцы должны иметь массу несколько граммов, хотя есть варианты приборов, рассчитанные на очень малые количества вещества. Точность анализа — 2–5 относительных процентов, длительность — от нескольких минут до 1–2 часов.
Помимо целей химического анализа, применение метода сыграло большую роль в исследовании самых различных свойств вещества. Так, благодаря рентгеновской спектроскопии получены
84
сведения о поведении и свойствах в твердых телах. Анализ рентгеновских спектров, обусловленных электронными переходами с глубинных дискретных уровней атомов на более удаленные орбиты, является наиболее прямым способом для изучения распределения энергетических уровней в валентной и проводящих зонах. Анализ дает также возможность найти распределение между и свободными электронными уровнями в твердых телах. При из-
менении физического или химического состояния вещества - на блюдаются небольшие смещения линий в спектрах отдельных элементов, которые позволяют судить о характере и изменении роли электронных орбиталей этих элементов при переходе в химически связанное состояние.
Электронно-зондовые микроанализаторы имеют много общих черт с растровыми электронными микроскопами. Конструктивные отличия обусловлены тем, что главным требованием к электронному микроскопу является обеспечение высокого пространственного разрешения, а основная цель при создании микроанализатора — достижение высокой чувствительности характеристическому рентгеновскому излучению и большой спектральной разрешающей способности.
Метод рентгеноспектрального микроанализа (РСМА) с помощью электронного зонда нашел широкое применение для решения многих проблем в электронной технике. РСМА позволяет:
—определять состав и распределение фаз при исследованиях диаграмм состояния сплавов, интерметаллических соединений, твердых растворов оксидов и других систем;
—анализировать неоднородности химического состава, определять наличие и распределение примесей, посторонних включений;
—исследовать процессы диффузии (например, при коррозии
илегировании полупроводников, спекании ферритов), электромиграцию атомов в электронных приборах;
—исследовать процессы выращивания и качества монокристаллов, тонких пленок, определять толщину последних;
—анализировать совершенство технологии изготовления интегральных микросхем и их дефекты.
Обработка информации, получаемой при комплексном исследовании методами РЭМ-РСМА, дает возможность достоверно оп-
ределять концентрацию различных фаз на зада поле, линейные размеры, периметр, площадь выделений, дефектов, аппликаций и других элементов структуры, толщину переходных слоев и т.д.
85
Важнейшими достоинствами РСМА являются неразрушающий характер исследования и возможность определения локального химического состава материала, благодаря использованию для возбуждения характеристического излучения тонкого электронного пучка, диаметр которого обычно составляет десятые доли микрона.
Виды анализа, проводимые с помощью рентгеноспектрального метода
При неподвижных образце и электронном зонде может быть проведен рентгеноспектральный анализ в выбранной точке. Этот анализ можно разделить на качественный и количественный. Качественный анализ проводится тремябами. Первый способ состоит в том, что записывается интенсивность излучения (величина сигнала) при одновременном сканировании кристаллдифракционного спектрометра по углам. Полученная запись расшифровывается, устанавливается соответствие пиков интенсивности спектральным линиям отдельных элементов, что позволяет определить качественный состав пробы.
При втором способе проводится последовательная настройка кристаллдифракционного спектрометра на максимумы аналитических линий отдельных элементов. Если необходимо определить наличие элемента, присутствующего в пробе в предельно малом количестве, производятся замеры интенсивностей излучения на угле, соответствующем максимуму аналитической линии, и на угле, где интенсивность должна соответствовать уровню фона.
Третьим способом является определение качественного состава пробы с помощью энергодисперсионного спектрометра. Этот способ позволяет получить качественный состав пробы за несколько минут, чего нельзя сделать первыми двумя способами. Однако разрешающая способность энергодисперсионного спектрометра ниже, чем кристаллдифракционного, поэтому в данном случае качественный анализ не всегда будет однозначен. Спектральные линии некоторых элементов могут настолько накладываться друг на друга, что не представится возможным ответить на
вопрос, какой элемент присутс в пробе. Такая неоднозначность наблюдается в группе редкоземельных элементов.
Все три способа качественного анализа могут быть автоматизированы с помощью компьютера. При этом в первом способе уже не проводится запись распределения интенсивности, а за определенное время измеряется интенсивность при шаговом сканировании спектрометра. Полученные значения выводятся на экран
86
вместе со значениями длин волн, углов или каких-либо других ве- |
|
|
||||||||||
личин, находящихся в прямой зависимости от длины волны для |
|
|
||||||||||
данной кинематической схемы спектрометра. |
|
|
|
|
|
|||||||
|
При втором способе качественного анализа в программе дол- |
|
|
|||||||||
жен быть предусмотрен вывод спектрометра на углы, соответст- |
|
|
||||||||||
вующие аналитическим линиям всех элементов. Значения этих уг- |
|
|
||||||||||
лов |
или |
|
каких-либо |
других |
|
величин, определяющих |
вывод |
|
|
|||
спектрометра |
|
на |
аналитическую |
, линиюзакладываются |
|
|
||||||
в базе данных. Медленное сканирование спектрометра в узком ин- |
|
|
||||||||||
тервале |
углов |
вблизи |
аналитической |
линии с |
замером- |
и |
||||||
тенсивности |
при |
каждом |
шаге |
и |
в тех случаях, когда интен- |
|
|
|||||
сивность |
в |
максимуме |
линии |
|
больше |
интенсивности, |
фона |
|||||
позволяет |
выдать сообщения |
о |
наличии |
данного элемента. |
||||||||
В фиксированной точке может быть проведен также количественный анализ.
Информация о распределении элементов
С помощью рентгеновского микроанализатора может быть получена информация о количественном и полуколичественном распределении элементов.
|
Полуколичественная информация содержится, прежде всего, |
||||
в |
растровых |
изображениях, по |
которым |
можно |
судить |
о том, в какой области больше, а в какой меньше определяемого элемента. Однако растровые изображения имеют заметный контраст только при достаточно большой разнице в интенсивностях между анализируемыми областями. Эта разница должна составлять не менее 30 % от большей из интенсивностей. Поэтому, например, на растровых изображениях чаще всего не удается -на блюдать неоднородность распределения основных легирующих элементов между составляющими дендритной структуры литых материалов. В то же время растровые изображения наглядно иллюстрируют распределение элементов между отдельными фазами неметаллических включений, в различных зонах биметалличе-
ских |
соединений |
в зонах избирательного окисления металла. |
|
Возможна также запись распределения |
интенсивности при |
сканировании электронного зонда вдоль спектральной линии(при вертикальном спектрометре) или вдоль направления, совпадающего с проекцией спектральной линии на плоскость образца(при наклонном спектрометре). В этом случае можно получить достоверную картину распределения элементов при сканировании электронного зонда в пределах примерно1 мм, чего вполне дос-
87
таточно при решении многих задач. Однако необходимое направление ориентации линии развертки должно иметь место для всех спектрометров. Только в этом случае можно получить правильный результат, изучая распределение одновременно нескольких элементов с помощью мно-
гоканального прибора. Известные в настоящее время модели рентгеновских микроанализаторов позволяют выполнить это -ус ловие не более чем для двух спектрометров одновременно. Поэтому исследование полуколичественного распределения при линейном сканировании электронного зонда проводится лишь в тех случаях, когда нет необходимости исследовать одновременно распределение нескольких элементов по всем каналам рентгеновского микроанализатора.
Наиболее надежная информация о количественном распределении элементов может быть получена при шаговом сканировании образца с измерением интенсивностей аналитических линий в каждой точке. Эти интенсивности сравниваются с интенсивностями на соответствующих стандартных образцах, затем после необходимых расчетов определяются концентрации элементов в каждой точке. Менее точную информацию о количественном распределении элементов вдоль какого-либо направления можно получить из записей, сделанных на диаграммной ленте, если там же записаны уровень интенсивности на стандартном образце и уровень интенсивности фона.
Информация о поверхности образца, полученная в растровом режиме
Микроструктура поверхности образца может быть изучена с
помощью растровых изображений во вторичных, поглощенных и |
|
||||||
обратнорассеянных электронах. Растровые изображения во вто- |
|
||||||
ричных |
электронах |
несут |
информацию |
о |
топографии |
||
поверхности. Поэтому для изучения тщательно отполированных |
|
||||||
шлифов, имеющих минимальный рельеф, целесообразнее исполь- |
|
||||||
зовать растровые изображения в поглощенных и обратнорассеян- |
|
||||||
ных электронах. Они в данном случае дают больше информации, |
|
||||||
поскольку чувствительны к среднему атомному номеру, т.е. к со- |
|
||||||
ставу. |
|
|
|
|
|
|
|
Локальность |
определяется |
размерами |
области |
образца, |
|||
в которой генерируется достаточно интенсивное анализируемое излучение. Она зависит от энергии первичных электроновЕ0, критической энергии возбуждения Ес, плотности образца и ряда других факторов. Например, для железа при Еа = 20 кэВ локальность со-
88
ставляет примерно 2,4 мкм. Минимальное разрешаемое расстояние в характеристическом излучении — около 0,5 мкм. Уменьшение диаметра зонда до
°
100 A не улучшает локальность анализа, но приводит к снижению интенсивности рентгеновского излучения.
Абсолютная чувствительность РСМА достигает10–12–10–16 .г Предел обнаружения элементов по концентрации зависит от -со става образца, локальности (или размеров анализируемых частиц), других условий эксперимента и ориентировочно составляет от 0,1 до 0,01 %. В редких случаях этот предел(при надежности 0,7) может быть снижен до 0,001 %.
Погрешность определения химического состава обычно не менее 2 % (в неблагоприятных случаях достигает 10 %).
В микроанализаторах используются спектрометры, оснащенные набором кристаллов-анализаторов, позволяющих регистриро-
°
вать излучение в интервале длин волн1,2 отдо 12 A . В этом интервале находятсяKа-линии элементов с атомными номерами от 11 до 32. Для анализа элементов с большими Z (вплоть до урана) используются линии L- и M-серий, попадающие в указанный интервал и имеющие меньшие значения Ес.
Длины волн Kа-линий легких элементов (с атомными номерами Z < 10) лежат за пределами спектрального диапазона, в котором эффективно работают применяемые в стандартных спектро-
метрах |
кристаллы-анализаторы. |
Однако |
использование |
||
пленочных псевдокристаллов и дифракционных решеток позво- |
|
||||
ляет |
расширить |
диапазон |
анализируемых |
элеме |
|
до бериллия. |
|
|
|
|
|
При проведении количественного микроанализа поверхность |
|
||||
образца должна быть гладкой и достаточно плоской, поскольку |
|
||||
рельеф и наклон поверхности сильно влияют на абсорбционную |
|
||||
поправку |
и коэффициент |
обратного |
рассеяния |
электронов. По- |
|
этому в РСМА используют высококачественные плоские шлифы.
Для исключения эффекта зарядки электронным лучом плохо проводящих образцов на их поверхность напыляют тонкую пленку углерода или алюминия(при этом, естественно, учитывается возможное влияние пленки на результаты анализа).
Исследования состава с помощью РСМА могут производиться в различных режимах.
Для проведения суммарного анализа, когда определяется
среднее (по площади) содержание элементов в образце, сканиро- |
|
||||
вание |
электронного |
луча |
производится |
при |
небольш |
увеличении по достаточно большому участку поверхности, содер- |
|
||||
жащему много характерных неоднородностей. При этом регистри- |
|
||||
руется |
число квантов аналитических линий за заданное время и |
||||
89
могут быть получены картины распределения элементов по - по верхности (фотографии в соответствующих характеристических лучах).
Выполнение локального (точечного) анализа осуществляется набором квантов излучений при фиксированной наводке электронного луча на определенную точку образца(например, на частицу включения или выделения второй фазы).
С целью изучения распределения концентрации элемента вдоль определенного направления(для проведения линейного анализа) регистрируется пиковая интенсивность характеристического излучения (скорость счета импульсов) при непрерывном медленном перемещении электронного зонда в этом направлении. Возможно также выполнение пошагового точечного анализа вдоль заданной траектории зонда.
3.6. Тонкопленочная рентгеновская дифрактометрия
Метод тонкопленочной рентгеновской дифрактометрии - по зволяет с помощью набора интенсивных линий производить прецизионные измерения периода кристаллической решетки и однозначно идентифицировать фазовый состав пленки. Оптическая схема тонкопленочного дифрактометра может быть реализована на дифрактометре типа «Дрон» (рис. 3.7).
При расположении подложки с пленкой под небольшим углом
a к падающему |
пучку |
эффективная глубина |
поглощения пучка |
||
hэфф = sin(a/m), |
где |
m |
— |
линейный |
коэффициент |
ослабления излучения, становится сравнимой с толщиной исследуемой пленки.
90
