15
5.5 Методы одномерной оптимизации
Методы минимизации функций одной переменной, кроме самостоятельного значения, часто являются важным элементом всевозможных методов минимизации функций нескольких переменных.
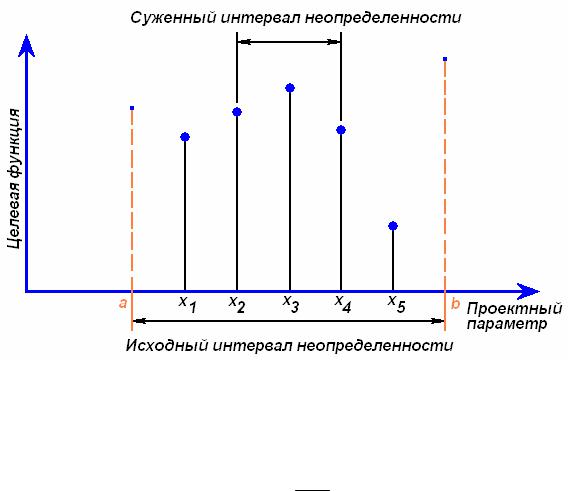
Задачу одномерной оптимизации можно представить следующим образом. Значения единственного проектного параметра х должны быть заключены в интервале а ≤ x ≤ b. Приступая к решению задачи, мы ничего не знаем о характере изменения целевой функции. Интервал значений х, в котором заключен оптимум, будем называть интервалом неопределенности. В начале процесса оптимизации интервал неопределенности имеет длину b - а (рис. 5.1).
Существует множество способов систематического сужения интервала неопределенности. Рассмотрим наиболее характерные методы оптимизации и отметим их главные особенности.
5.5.1 Метод общего поиска
Наиболее простым способом сужения интервала неопределенности для одномерной целевой функции является метод общего поиска. При этом интервал неопределенности (рис. 5.8) делится на N равных частей с последующим вычислением значений целевой функции в полученных узлах сетки и выборе из них
минимального (или максимального).
Рисунок 5.8 - Метод общего поиска (ищем максимум)
В результате интервал неопределенности сужается до двух шагов сетки.
Обычно говорят о дроблении интервала неопределенности, которое характеризу-
ется коэффициентом f. Разделив интервал неопределенности на N частей, по-
лучим N+1 узел, и тогда коэффициент дробления для метода общего поиска f = N2+1 .
Чтобы получить значение f = 0.01, потребуется вычислить целевую функцию в 199 точках, а при f = 0.001 уже N = 1999. Несложно заметить, что эффективность метода общего поиска при уменьшении интервала неопределенности стремительно падает.
16
Можно модифицировать метод общего поиска следующим образом. Чтобы получить коэффициент дробления f = 0.01, вычислим сначала функ-
цию в 19 точках и получим f = 0.1. Затем, вычислив еще 19 значений функции на сокращенном интервале неопределенности, получим f = 0.01. Таким образом, по-
требуется всего 38, а не 199 вычислений.
Несмотря на очень низкую эффективность, метод общего поиска имеет важное достоинство – используемая целевая функция может быть неунимодаль-
ной и иметь разрывности.
5.5.2 Метод золотого сечения
Наиболее эффективным методом одномерной оптимизации считается ме-
тод Фибоначчи [1]. Лишь немногим ему уступает метод золотого сечения [1], ко-
торый существенно проще в организации вычислительного процесса и потому нашел большее распространение.
При использовании метода золотого сечения целевая функция обяза-
тельно должна быть унимодальной.
В методе золотого сечения целевая функция вычисляется в точках интервала неопределенности, расположенных таким образом, чтобы каждое вычислен-
ное значение целевой функции давало новую полезную информацию.
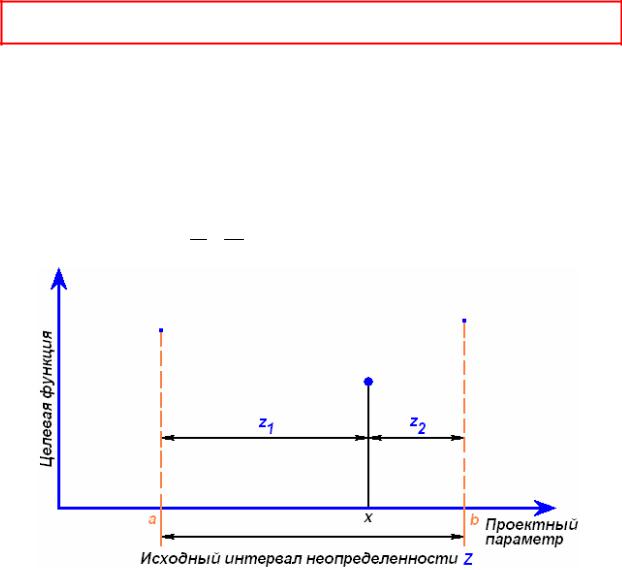
Сущность этого метода состоит в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большого отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего отрезка. На рис. 5.9 показан интервал неопределенности Z, состоящий из отрезков z1 и z2, отношение длин которых определяется правилом золотого сечения
z1 = z2 , и, кроме того, z1 + z2 = Z.
Z z1
Рисунок 5.9 - Обозначения, используемые в методе золотого сечения
17
Из первого уравнения следует z12 = Z·z2. Подставляя сюда значение Z из второго уравнения, и деля затем обе части на z12, получаем
|
z2 |
2 |
|
z2 |
|
|
|
|
|
||
|
+ |
z −1 = 0. |
|||
z |
|
||||
|
1 |
|
|
1 |
|
Решая это квадратное уравнение, определяем для положительного корня |
|||||
значение |
|
|
|
|
|
r = z2 |
= −1 + |
5 = 0.6180339. |
|||
z |
|
|
2 |
|
|
1 |
|
|
|
|
|
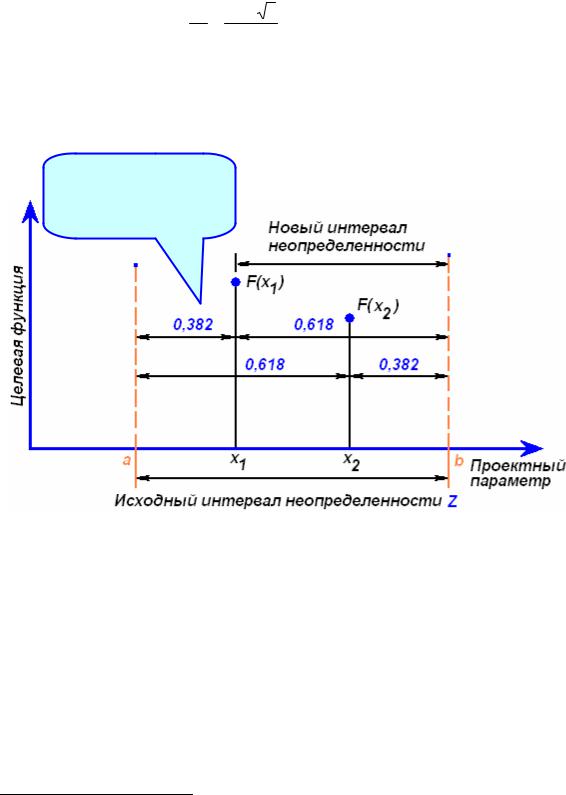
На рис. 5.10 изображено деление интервала неопределенности двумя симметрично расположенными точками x1 и x2 в «золотом» отношении:
x1 = a +(1 −r()(b −a))≈ a +0.382((b −a))= a +0.382 Z ;. x2 = a +r b −a ≈ a +0.618 b −a = a +0.618 Z .
Так как F(x1) > F(x2),
то отбросим интервал a .. x1, перенеся a x1
Рисунок 5.10 - Метод золотого сечения (ищем минимум)
В точках x1 и x2 вычисляются значения целевой функции F(x1) и F(x2). Сравнение этих значений5 дает возможность отбросить либо интервал [a .. x1], либо интервал [x2 .. b]. Так если на рис. 5.10 мы ищем минимум и F(x1) > F(x2), то следует отбросить интервал [a .. x1]. При каждом таком отбрасывании исходный ин-
тервал неопределенности уменьшается в 1 / 0.618 раза.
На новом интервале неопределенности уже существует одна точка, полученная на предыдущем шаге и осуществляющая его золотое сечение. Таким об-
разом, начиная со второго шага, следует вычислять лишь одно новое значение
целевой функции в недостающей точке нового интервала неопределенности. Положение этой точки определяется правилом золотого сечения по приведенным
выше формулам.
5 Напомним – функция унимодальная!