Конспект лекций Глазова / 4.5. Нормальная система

4.5. Нормальная система.

Причины того, что одномерное и многомерные нормальные распределения играют центральную роль в теории вероятностей и ее приложениях, указаны в п. 3.8. В данном пункте мы дадим вид N-мерной нормальной плотности и N-мерной характеристической функции и рассмотрим частный случай нормальной системы при N=2.

Нормальная система случайных величин - одна из немногих систем, для которых возможна компактная запись N-мерной плотности для любого конечного N. Для этого используются векторно-матричные обозначения.

Определение. Система X=(X₁, X₂, ... X_N)^T случайных величин называется нормальной системой порядка N (N=1, 2, ...), если N-мерная плотность вероятности системы имеет вид

f(x)=(2)-N/2(detK)-1/2exp[-(x-m)TK-1(x-m)],

(4.5.1)

где x - вектор-столбец значений: x={x_i}, i=1, 2, ... , N; m - вектор-столбец математических ожиданий: m={m_i}, i=1, 2, ... , N; верхний индекс Т обозначает транспонирование; K - ковариационная матрица порядка (NN): K={K_ks}, k,s=1, 2, ... , N; K_k,s - ковариация (второй смешанный центральный момент) между X_k и X_s; detK - определитель (детерминант) матрицы K. Нормальная система называется невырожденной, если матрица K не вырождена (не особенная), т. е. detK>0 (известно, что ковариационная матрица симметричная и неотрицательно определенная, т. е. ее определитель не принимает отрицательных значений); нормальная система называется вырожденной, если матрица K вырождена (особенная), т. е. detK=0 (в этом случае xL_M , где L_M - линейное подпространство (гиперплоскость) размерности M<N). В выражении (4.5.1) уже предполагается, что K не вырождена, т. к. обратная матрица K^-1 cуществует только при этом условии.

Квадратичная форма в показателе экспоненты неотрицательно определенная в силу положительной определенности K:

(x-m)^TK^-1(x-m)0,

значит показатель экспоненты всюду неположителен. Отсюда следует, что f(x) принимает максимальное значение

f_max=(2)^-N/2(detK)^-1/2

в точке x=m , имеющей смысл «центра тяжести» системы. Можно показать, что плотность (4.5.1) правильно нормирована, т. е. N-мерный интеграл

=1.

Если N-мерную плотность проинтегрировать по совокупности M<N переменных, то получится нормальная плотность (N-M) остальных переменных вида (4.5.1), с невырожденной ковариационной матрицей порядка [(N-M)(N-M)]. Это означает, что в нормальной системе N-го порядка подсистемы любого меньшего порядка также нормальны. Характеристическая функция N-мерной системы равна

(v)=exp(iv^Tm-v^TKv).

Как следует из определения (4.4.12) коэффициента корреляции,

K_k,s=,

где - среднеквадратичное отклонение величины X_s , r_k,s - коэффициент корреляции величин X_k, X_s . При k=s получаем r_k,k=1 (поскольку СВ полностью коррелирована с собой), и K_k,k=D_k (дисперсия величины X_k), т. е. диагональные элементы матрицы K суть дисперсии величин системы. Теперь можно подсчитать число S параметров в N-мерном распределении. Рассматривая в качестве параметров математические ожидания, среднеквадратичные отклонения и коэффициенты корреляции, получаем: N величин m_k , (k=1, 2, ..., N), N величин , N(N-1)/2 величин r_k,s (по числу пар в системе), итого S=N(N+3)/2. Например, при N=1 S=2, при N=2 S=5 и т. д.

Очевидно, N-мерная нормальная плотность (4.5.1) факторизуется на N одномерных (частных) плотностей тогда и только тогда, когда матрица K диагональна, т. е. когда все ковариации K_k,s=0 и, следовательно, все коэффициенты корреляции r_k,s=0 при ks. Отсюда следует очень важный вывод: в нормальной системе корреляция эквивалентна зависимости, т. е. из независимости следует некоррелированность (это верно для всех систем), а из некоррелированности - независимость (это специфическое свойство нормальных систем). Это одно из тех замечательных математических свойств, благодаря которым нормальные системы играют столь важную роль. В частности, из этого свойства, в свою очередь, следует, что все четные центральные моменты нормальной системы выражаются через ковариации (нечетные моменты равны нулю вследствие симметрий).

Следует иметь в виду одну тонкость. Нередко полагают, что система случайных величин нормальна, если нормальны все ее одномерные частные распределения. В общем случае это неверно. Как указано выше, из нормальности системы следует нормальность всех подсистем, в том числе - одномерных. Однако из нормальности одномерных подсистем еще не следует нормальности всей системы: N-мерная плотность при N>1 может при этом не иметь вида (4.5.1).

N-мерную нормальную плотность можно записать и в поэлементном виде. Учтя известную из линейной алгебры формулу для обратной матрицы:

K^-1=A^T/detK,

где A={A_k,s} - матрица алгебраических дополнений, и симметричность K, можем переписать (4.5.1) в виде

f(x)=(2)-N/2(detK)-1/2exp[-(2detK)-1(xk-mk)Ak,s(xs-ms)].

(4.5.2)

Распределение нормальной системы при N=1 есть просто одномерное нормальное распределение, рассмотренное в п. 3.8. Теперь рассмотрим двумерную нормальную систему (X₁, X₂). Ковариационная матрица при N=2 имеет вид

K=,

где r=r₁₂ - единственный коэффициент корреляции в системе. Найдя матрицу алгебраических дополнений

A=,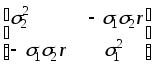

и определитель

detK=,

из (4.5.2) находим:

f(x, y),

где для удобства геометрической интерпретации проведены очевидные переобозначения.

В соответствии с формулой для S, в этом распределении 5 параметров: математические ожидания m_x , m_y , с. к. о. , и коэффициент корреляции r между X и Y. Поэтому можно кратко записывать двумерную нормальную плотность в виде

f(x, y)=N(m_x , m_y , ),

указывая в скобках численные значения параметров. Например,

N(0, -2, 3, 1, -0.5) - это двумерная нормальная плотность с параметрами m_x=0, m_y=-2, , r=-0.5.

Убедимся в том, что частные одномерные плотности этой системы суть одномерные нормальные распределения вида, рассмотренного в п. 3.8. Имеем:

,

где

.

Обозначив

,

приведем интеграл к виду

.

Дополнив показатель степени до полного квадрата и заменой переменных приведя интеграл к виду интеграла Пуассона (см. п. 3.8), в результате получим

,

откуда

,

т. е.

,

что совпадает с обычным выражением одномерной нормальной плотности (см. п. 3.8). Аналогичным образом можно показать, что

.

Т. о., частные плотности двумерной нормальной системы суть обычные нормальные плотности N(m_x , ), N(m_y , ).

Точка с координатами (m_x , m_y) иногда называется центром рассеивания. Пусть X и Y некоррелированы; тогда, положив в f(x, y) r=0, получаем

,

т. е. двумерная плотность факторизовалась, следовательно, величины Х, Y при r=0 стали независимыми. Т. о., мы еще раз убедились, что в нормальной системе из некоррелированности следует независимость.

При r0 f(x, y) не факторизуется, следовательно, величины Х, Y зависимы; эту зависимость можно проанализировать, если найти условные плотности. Имеем:

,

и аналогичным образом,

.

Обозначив

my/x=my+r(x-mx),	(4.5.3)
,	(4.5.4)

первую условную плотность можно привести к виду

f(y/x)=,

(4.5.5)

а обозначив

mx/y=mx+r(y-my),	(4.5.6)
,	(4.5.7)

вторую условную плотность можно привести к виду

f(x/y)=.

(4.5.8)

Мы видим, что условные плотности нормальны с математическими ожиданиями m_y/x , m_x/y и с.к.о. .

В соответствии со сказанным в п. 4.4, зависимость m_y/x от х задает регрессию Y на X, а зависимость m_x/y от у - регрессию Х на Y. Из (4.5.3) видно, что регрессия Y на X геометрически выглядит как прямая, проходящая через точку (m_x , m_y) с угловым коэффициентом r, а регрессия Х на Y - как прямая, проходящая через точку

(m_x , m_y) с угловым коэффициентом . Т. о. в нормальной системе обе регрессии линейны, причем линии регрессии в общем случае не совпадают: при полной корреляции (r=1) они совпадают, при независимости Х, Y они параллельны осям координат, при частичной корреляции (-1<r<1) они пересекаются в центре рассеяния (m_x , m_y). В общем случае (в не нормальных системах) в отношении формы регрессий могут быть разные варианты: одна из регрессий линейна, другая - нелинейна; обе нелинейны. В случае, если регрессия линейна, угловой коэффициент прямой регрессии называется коэффициентом регрессии.

Из (4.5.4) и (4.5.7) следует, что в нормальной системе условные дисперсии не зависят от условий; такие регрессии называются однородными. Т. о. зависимость в двумерной нормальной системе характеризуется тем, что обе условные плотности нормальны, обе регрессии - линейны и однородны.

Из выражения двумерной плотности видно, что поверхность функции f(x, y) имеет колоколообразный вид с единственным максимумом

f_max=

в точке (m_x , m_y) (поскольку квадратичная форма в квадратных скобках неотрицательно определенная, т. е. не принимает отрицательных значений). Рассекая эту поверхность горизонтальными плоскостями и проектируя линии пересечения на плоскость XOY, получим линии равных плотностей. Уравнение семейства этих линий получим, положив f(x, y)=const, т. е.

,

(4.5.9)

где 0<< - константа: чем больше ее величина, тем ниже секущая плоскость и шире область, охватываемая линией равной плотности; при 0 эта область стягивается в точку. Семейство (4.5.9) - это семейство эллипсов с одним и тем же центром и одними и теми же осями: центр каждого эллипса находится в точке (m_x , m_y), оси эллипсов составляют с осью ОХ углы, определяемые уравнением

tg2.

(4.5.10)

Это уравнение имеет два корня , различающихся на , что понятно, т. к. оси эллипса взаимно перпендикулярны. По какой из осей эллипсы вытянуты больше - очевидным образом зависит от соотношения . Из (4.5.10) видно, что ориентация эллипсов относительно координатных осей зависит от коэффициента корреляции r: если X, Y некоррелированы (т. е. в данном случае и независимы), то оси эллипсов параллельны координатным осям; в противном случае они составляют с координатными осями некоторый угол. Рассмотренные эллипсы равной плотности иногда называют эллипсами рассеивания, а их оси - главными осями рассеивания.