Конспект лекций Глазова / 5.4.1. Распред ф-ции случ аргументов

5.4. Распределение функции случайных аргументов.

Пусть имеется n-мерная функция Y=(X) m-мерного случайного аргумента Х, причем Х и Y - непрерывные СВ. Для исчерпывающего описания вектора Y по характеристикам вектора Х требуется решить наиболее сложную задачу: по плотности f_x(x) найти плотность f_y(y). Мы рассмотрим самые простые варианты этой задачи: а) когда Х и Y одномерны; б) когда Х двумерный, Y - одномерный; в) когда Х многомерный с независимыми компонентами, Y - одномерный.

5.4.1. Распределение одномерной функции

одного случайного аргумента.

Постановка задачи: Y=(X), известна функция (.) и дана плотность f_x(x), требуется найти плотность f_y(y).

Известно, что если функция монотонна, то обратная функция однозначна, в противном случае обратная функция не однозначна. При этом число ветвей однозначности обратной функции может зависеть от y. Рис 5.4.1 иллюстрирует это свойство: функция не монотонна, обратная функция не однозначна, причем при она имеет 3 ветви однозначности, при y<1.368869 и при y>4.112611 - одну ветвь однозначности.

Рисунок 5.4.1.

График функции y=.

Локальный минимум: х₁=0.548584, y₁=1.368869;

локальный максимум: x₂=-1.215251, y₂=4.112611.

Предположим сначала, что функция (.) однозначна и монотонна в области, где f_x(x)>0. Тогда обратная функция однозначна и монотонна. Монотонная функция может быть возрастающей или убывающей.

А) Пусть (.) - монотонно возрастающая функция. Тогда и обратная функция (.) - монотонно возрастающая функция, т. е. значениям СВ Y, меньшим, чем y, соответствуют значения СВ Х, меньшие, чем

x=(y).

Поэтому

F_y(y)=P(Y<y)=P(X<x)=F_x(x)==F_x[(y)],

или

Fy(y)=Fx[(y)].

(5.4.1)

Равенство (5.4.1) показывает, как найти функцию распределения F_y(y) величины Y, если известна функция распределения F_x(x) величины Х: для этого надо в F_x(x) подставить вместо х выражение (у). Дифференцируя (5.4.1) по у, используя правило дифференцирования сложной функции, находим:

f_y(y)=,

или

fy(y)=fx[(y)] .

(5.4.2)

Б) Пусть теперь (.) - монотонно убывающая функция. Тогда и обратная функция (у) - монотонно убывающая, т. е. значениям величины Y, меньшим, чем у, соответствуют значения величины Х, большие, чем x=(y). Поэтому

F_y(y)=P(Y<y)=P(X>x)=1-P(X<x)=1-F_x(x)=1-F_x[(y)],

или

Fy(y)=1-Fx[(y)].

(5.4.3)

Дифференцируя это равенство по у, находим:

fy(y)=-fx[(y)] .

(5.4.4.)

Объединим формулы (5.4.2) и (5.4.4) в одну формулу, учтя, что при возрастающей (.) и (.) - возрастающая, поэтому >0; а при убывающей (.) и (.) - убывающая, поэтому <0. В итоге получаем формулу

fy(y)=fx[(y)] ,

(5.4.5)

справедливую для любой монотонной функции (.).

Теперь пусть функция (.) однозначна и не монотонна в области, где f_x(x)>0. Тогда обратная функция (.) неоднозначна в области, где f_y(y)>0, т. е. одному значению у соответствует несколько ветвей функции (y). Обозначим эти ветви _k(y), (k=1, 2, ..., s(y)), где s - число ветвей, и учтено, что s может зависеть от у. Суммируя элементы вероятности f_y(y)dy по каждой из ветвей, можно показать, что

fy(y)=.

(5.4.6)

Эта формула дает общее решение задачи, в частном случае монотонной функции (.) из нее следует более простая формула (5.4.5).

До сих пор не конкретизировались ни функция (.), ни плотность f_x(x), в этом смысле получен общий результат поставленной задачи. Теперь в качестве полезных и поучительных упражнений рассмотрим некоторые частные случаи, конкретизируя сначала функцию (.), а затем и плотность f_x(x).

Линейная функция. Пусть

Y=aX+b.

(5.4.7)

Функция монотонна; определив

y=(x)=ax+b; x=(y)=(y-b)/a; ; ,

из (5.4.5) получаем

fy(y)=fx(.

(5.4.8)

В частном случае а=1 из этой формулы находим, что если Y=X+b, то f_y(y)=f_x(y-b), тем самым подтверждая то, что уже неоднократно имели в виду: при прибавлении к случайной величине постоянной плотность вероятности сдвигается по оси абсцисс на эту постоянную.

Квадратичная функция. Пусть

Y=X2.

(5.4.9)

Функция (.) не монотонна, обратная функция - не однозначна. Имеем

y=(x)=x²; x=(y)=, ,

т. е. обратная функция имеет две ветви:

Подставляя найденное в (5.4.6), находим:

или

(5.4.10)

Линейная функция нормальной случайной величины. Пусть Y связана с Х линейно выражением (5.4.7), и Х - нормальная случайная величина с плотностью

.

(5.4.11)

Подставляя это выражение в (5.4.8), получаем:

.

Как показано в п. 5.3, среднее, дисперсия и с. к. о. линейной функции (5.4.7) одного случайного аргумента равны

my=amx+b,	(5.4.12)
Dy=a2Dx , ;	(5.4.13)

с учетом этих равенств f_y(y) перепишется в виде

,

т. е. распределение линейной функции нормального случайного аргумента также нормально с соответствующими математическим ожиданием и с. к. о. Этот вывод - частный случай более общей закономерности: n-мерная линейная функция m-мерного нормального аргумента также нормальна.

Квадратичная функция нормальной случайной величины. Пусть Y связана с Х квадратично выражением (5.4.9), и Х - нормальная СВ с плотностью (5.4.11). Используя (5.4.10), имеем:

или

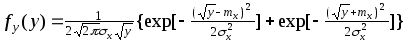, y0.

В частном случае, когда =1, эта плотность имеет вид

, y0,

и представляет т. н. нецентральное -распределение с одной степенью свободы (читается: «хи-квадрат-распределение...»). В еще более частном случае, когда m_x=0, =1, и Х имеет каноническое нормальное распределение

,

Y имеет плотность

, y>0,

представляющую т. н. центральное -распределение с одной степенью свободы.