Конспект лекций Глазова / 4.1.Распр системы СВ

4. Системы случайных величин.

Часто нас интересует не одна, а одновременно несколько СВ. Приведем примеры.

а) При радиолокационном обнаружении самолета нас могут интересовать дальность и две угловые координаты этого самолета, т. е. 3 СВ.

б) Пусть изучается поведение сигнала от удаленной радиостанции и измеряются значения амплитуды сигнала в N разнесенных моментах времени; это N СВ.

в) Производятся опытные артиллерийские стрельбы; точка разрыва снаряда представлена двумя СВ - координатами этой точки.

г) Дискретизированное черно-белое изображение представлено яркостями в каждом из M пикселов; в общем случае эти яркости суть M СВ.

Набор одновременно рассматриваемых СВ называется системой случайных величин. Систему n случайных величин можно представлять как одну многомерную (n-мерную) СВ. Значением n-мерной СВ является упорядоченный набор n чисел - значений одномерных СВ, составляющих систему. Эти n чисел соответствуют точке или вектору в n-мерном пространстве. Поэтому многомерную СВ иногда называют случайным вектором.

Можно было бы попытаться дать описание каждой из СВ, составляющих систему, в отдельности, используя методы, рассмотренные выше. Однако, при этом мы потеряем информацию о взаимозависимости между этими СВ. Существуют такие общие методы описания системы СВ, которые одновременно дают информацию как о свойствах каждой из СВ, входящих в систему, так и о их взаимной зависимости.

4.1. Распределение системы.

Также как одномерные СВ, многомерные СВ могут быть непрерывными, дискретными или смешанными. Ниже мы рассмотрим только непрерывные СВ. Значения n-мерной непрерывной СВ плотно заполняют область или систему областей n-мерного пространства и составляют несчетное множество. Поэтому, как и в одномерном случае, вероятность каждого отдельного значения многомерной СВ равна нулю, и для описания ее вероятностных свойств необходимо прибегнуть к характеристикам, аналогичным одномерной функции распределения и одномерной плотности вероятности.

Начнем с двумерной СВ. Она представлена парой (X, Y) одномерных СВ X и Y, значения двумерной СВ - пары (x, y) вещественных чисел. Исчерпывающей и универсальной характеристикой двумерной СВ (справедливой также и для дискретной, и для смешанной СВ) является функция распределения двумерной СВ (или двумерная функция распределения)

F(x, y)=P(Xx, Yy),

(4.1.1)

рассматриваемая как функция текущих значений x, y составляющих СВ. Величина в правой части равенства геометрически означает вероятность попадания случайной точки (X, Y) в полубесконечный «угол» с вершиной (x, y); функциональная зависимость этой вероятности от координат вершины «угла» и есть двумерная функция распределения.

Определение. Двумерная СВ (двумерная система СВ) называется непрерывной, если F(x, y) всюду непрерывна по обоим аргументам.

Двумерная функция распределения имеет следующие свойства.

1. F(x, y) всюду неотрицательна как имеющая смысл вероятности.

2. F(x, y) всюду неубывающая по обоим аргументам. Действительно, если один из аргументов (или оба) увеличит свое значение, «угол» расширится и вероятность попадания в него увеличится или останется той же, но не уменьшится.

3. . Действительно, при или «угол» с вершиной (x, y) исчезает и вероятность попадания в него стремится к нулю.

4.

,

(4.1.2)

где F_x(x), F_y(y) - в общем случае различные (поэтому снабжены индексом) функции распределения одномерных СВ, входящих в систему. Другими словами, при стремлении одного из аргументов к бесконечности, двумерная функция распределения превращается в одномерную, соответствующую другому аргументу. Доказательство: поскольку события (Y) и (X) достоверны, и учитывая, что для любого события A P(AD)=P(A) (D - достоверное событие), имеем:

;

.

5.

(4.1.3)

Действительно, если одновременно , то «угол» с вершиной (x, y) расширяется до всей плоскости XOY и вероятность попадания в него стремится к единице.

Напомним, что непрерывная функция двух переменных геометрически представляет собой поверхность. Поверхность функции распределения - это «горка», не опускающаяся ниже координатной плоскости XOY, начинающаяся с уровня «0» в бесконечной «дали» третьего квадранта этой плоскости, приходящая к уровню «1» в бесконечной «дали» первого квадранта, нигде не опускающаяся в положительном направлении координат x и y, имеющая горизонтальные участки над областями плоскости XOY, в которых отсутствуют значения двумерной СВ, а над остальными областями имеющая положительный наклон.

Другая характеристика двумерной СВ, плотность вероятности, не универсальна - она существует только для непрерывной СВ и не обязательно во всех точках. Рассмотрим точку с координатами (x, y) и ее малую окрестность. Если в этой точке существует производная

,

(4.1.4)

то ее можно рассматривать как вероятность на единицу площади в окрестности этой точки и назвать двумерной плотностью вероятности. Тогда вероятность попадания в элементарный прямоугольник со сторонами dx, dy в окрестности точки (x, y) равна

dP=f(x, y)dxdy,

(4.1.5)

и называется двумерным элементом вероятности. Очевидно, вероятность попадания в любую область E на плоскости XOY равна сумме элементов вероятности по точкам этой области, т. е.

,

(4.1.6)

причем этот интеграл имеет смысл интеграла Римана, если мы предположим, что функция распределения F(x, y) не дифференцируема не более чем в счетном числе точек. Более того, в этом случае интеграл сходится и не превосходит единицы как имеющий смысл вероятности. Взяв в (4.1.6) в качестве Е прямоугольник, имеем

.

(4.1.7)

Устремив в этом равенстве , получаем

и изменив в последнем равенстве обозначения, запишем его в виде

.

(4.1.8)

Дифференцируя обе части этого равенства по x и по y, снова получаем (4.1.4).

Таким образом, зная функцию распределения, можно найти плотность вероятности как вторую смешанную производную (равенство (4.1.4)), и наоборот, зная плотность, найти функцию распределения как интеграл по (4.1.8). Взаимно-однозначная связь между F(x, y) и f(x, y) означает, что они несут эквивалентную информацию о статистических свойствах двумерной СВ (X, Y).

Как функция f(x, y) имеет следующие свойства:

1. f(x, y)0 всюду, где она определена; действительно, в силу (4.1.4) f(x, y) есть производная от всюду неубывающей функции F(x, y).

2. В силу (4.1.3)

,

т. е. интеграл от f(x, y) по всей плоскости XOY равен 1 (условие нормировки).

3.

,

(4.1.8)

где f_x(x), f_y(y) - одномерные плотности вероятности случайных величин X и Y, составляющих систему (могут быть разными функциями, поэтому снабжены индексом). Действительно, комбинируя (4.1.2) и (4.1.8), запишем:

и дифференцируя первое равенство по x, а второе - по y, получаем равенства (4.1.8).

Как всякая функция двух переменных, f(x, y) геометрически может быть представлена поверхностью над плоскостью XOY. Перечисленные свойства означают, что вся эта поверхность расположена не ниже плоскости XOY, объем, заключенный между поверхностью и этой плоскостью, равен единице, а зависимость площадей сечений, перпендикулярных одной оси, от значений на этой оси дает соответствующую частную плотность вероятности.

Двумерная характеристическая функция определена как двумерное преобразование Фурье от двумерной плотности вероятности:

,

(4.1.9)

а обратное преобразование Фурье дает

.

(4.1.10)

В дальнейшем f_x(x), f_y(y) будем называть частными плотностями вероятности системы, F_x(x), F_y(y) - частными функциями распределения системы, - частными характеристическими функциями системы, а представленные ими одномерные распределения - частными распределениями системы. Свойства (4.1.2) двумерной функции распределения и свойства (4.1.8) двумерной плотности вероятности показывают, что двумерное распределение несет всю информацию о частных распределениях, т. к. из двумерных характеристик всегда можно найти частные (одномерные) характеристики. Обратное неверно: как выяснится в дальнейшем, знания частных распределений в общем случае недостаточно для получения двумерного распределения.

Введенные характеристики и их свойства легко обобщаются на случай любого конечного числа случайных величин в системе. Пусть имеется система (X₁ , X₂ ,...,X_n) n случайных величин, ее можно назвать n-мерной СВ. n-мерной функцией распределения называется функция n аргументов, определяемая как

;

n-мерная плотность вероятности f(x₁, x₂, ..., x_n), в тех точках n-мерного пространства, где она существует, представляет собой вероятность на единицу n-мерного объема в окрестности точки (x₁, x₂, ..., x_n) и связана с функцией распределения соотношениями

,

(4.1.11)

.

(4.1.12)

Функция F(x₁,x₂,...,x_n) всюду неотрицательна, не убывает по всем аргументам, всюду на равна нулю, при стремлении всех аргументов к бесконечности стремится к единице (условие нормировки). Если в n-мерной функции распределения какие-то k аргументов положить равными бесконечности (k<n), то получится (n-k)-мерная функция распределения остальных случайных величин. Функция f(x₁,x₂,...,x_n) всюду неотрицательна, n-мерный интеграл от нее по всем аргументам равен единице (условие нормировки); если ее проинтегрировать по каким-то k аргументам (k<n), то получится (n-k)-мерная плотность вероятности остальных случайных величин. n-мерная характеристическая функция всюду конечна и связана с n-мерной плотностью парой n-мерных преобразований Фурье.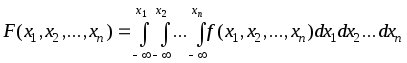