Конспект лекций Глазова / 4.4. Завис и независ случ вел

4.4. Зависимость и независимость случайных величин.

Причиной совместного рассмотрения нескольких СВ послужил тот факт, что раздельное описание случайных величин не дает информации об их взаимозависимости. Между тем, эта информация часто не только существенна, но и наиболее важна. Зависимость между случайными величинами (статистическая зависимость) имеет более общий характер, чем обычная функциональная зависимость между детерминированными величинами; последняя представляет собой частный случай статистической зависимости. Мы изучим статистическую зависимость на примере непрерывной двумерной СВ. Сначала рассмотрим статистическую зависимость общего вида, затем т. н. линейную статистическую зависимость (корреляцию).

4.4.1. Статистическая зависимость общего вида.

Рассмотрим непрерывную двумерную систему (двумерную СВ) (X, Y). Статистические свойства этой системы исчерпывающим образом описываются плотностью вероятности f(x, y) и/или функцией распределения F(x, y). Из них однозначно следуют частные плотности f_x(x), f_y(y) и частные функции распределения F_x(x), F_y(y), но не обязательно наоборот, т. к. частные распределения не содержат информации о статистической зависимости между X и Y (см. п. 4.1). Пусть Y приняла значение y₁; распределение величины X при этом условии задается плотностью вероятности, которую обозначим f(x/y₁) и назовем условной плотностью вероятности X при условии, что Y=y₁. Аналогично, если Y приняло значение y₂, то имеем условную плотность f(x/y₂), если Y=y₃, то f(x/y₃) и т. д. Вообще Y может принимать одно из несчетного множества значений, поэтому в условии Y=y можно считать y переменной, а в соответствующей условной плотности f(x/y) будет две переменных: x и y. Очевидно, что если функция двух переменных f(x/y) на самом деле не зависит от у, то f(x/y)=f_x(x), т. е. условная плотность величины Х тождественно (т. е. при всех возможных х, у) равна ее частной (безусловной) плотности. В противном случае, если имеется какая-то зависимость условной плотности от у, то f(x/y) не может быть тождественно равной f_x(x), так как при разных у зависит от х, вообще говоря, по-разному.

Определение. X называется независимой от Y, если при всех возможных х, у f(x/y) не зависит от у, и, как следствие, f(x/y)=f_x(x). В противном случае, Х называется зависимой от Y, и, как следствие, f(x/y) - функция двух переменных и не может тождественно равняться частной плотности Х.

Аналогичным образом, зафиксировав значение Х=х, рассмотрим условную плотность f(y/x); если она не зависит от х, то Y называется независимой от Х, при этом f(y/x)=f_y(y). Если же f(y/x) зависит от х, то Y зависит от Х, при этом f(y/x)f_y(y).

Условные плотности f(x/y), f(y/x) не следует путать с частными (безусловными) плотностями f_x(x), f_y(y): частная плотность f_x(x) описывает СВ X в отдельности, в отсутствии какой-либо информации о СВ Y; аналогично, частная плотность f_y(y) описывает СВ Y в отдельности, в отсутствии какой-либо информации о СВ X. Пусть, например, мы изучаем рост X (см) и вес Y (кг) мужчин как случайные величины. Если мы соберем данные о росте всех мужчин вне зависимости от их веса, то можем приближенно получить f_x(x); если соберем данные о весе всех мужчин вне зависимости от их роста, то можем приближенно получить f_y(y). Если же мы отберем мужчин ростом примерно 170 см и измерим их веса, то получим приближенно f(y/170); если отберем мужчин весом примерно 80 кг и измерим их рост, то получим приближенно f(x/80). Также не следует путать аргумент условной плотности с величиной, задающей условие: первый находится в числителе «косой» дроби, вторая - в знаменателе.

Условные плотности вероятности удовлетворяют обычным требованиям: f(x/y)0 при всех х и всех допустимых y; f(y/x)0 при всех y и всех допустимых х;

,

- условия нормировки; элементы условной вероятности:

P[X(x, x+dx); Y=y]=f(x/y)dx, P[Y(y, y+dy); X=x]=f(y/x)dy;

условные вероятности попадания в конечный интервал:

P[X(a, b); Y=y]=, P[Y(c, g); X=x]=.

Как и в безусловных распределениях, наряду с условными плотностями существуют условные функции распределения

F(x/y)=P(Xx; Y=y), F(y/x)=P(Yy; X=x),

взаимно-однозначно связанные с условными плотностями:

Рассмотрим элементарный прямоугольник П со сторонами dx, dy в окрестности точки (x, y), и найдем вероятность попадания в этот прямоугольник двумя способами. Первый:

P[(X, Y)П]=f(x, y)dxdy;

второй:

P[(X, Y)П]=P[X(x, x+dx)] P[Y(y, y+dy)/X=x]=

=[f_x(x)dx] [f(y/x)dy]=f_x(x)f(y/x)dxdy.

Приравнивая результаты, получаем

f(x, y)=fx(x)f(y/x).

(4.4.1)

Реализуя второй способ в другом порядке:

P[(X, Y)П]=P[Y(y, y+dy)] P[X(x, x+dx)/Y=y]=

=[f_y(y)dy] [f(x/y)dx]=f_y(y)f(x/y)dxdy,

получаем

f(x, y)=fy(y)f(x/y).

(4.4.2)

Приравняем правые части формул (4.4.1) и (4.4.2):

fx(x)f(y/x)=fy(y)f(x/y).

(4.4.3)

Т. о. двумерная плотность равна произведению частной плотности одной СВ на условную плотность другой, причем оба варианта этого произведения эквивалентны.

Установим теперь два важных свойства. Пусть Х не зависит от Y, тогда f(x/y)=f_x(x); подставив это равенство в (4.4.3) и считая, что f_x(x)0, получаем f(y/x)=f_y(y), т. е. Y не зависит от Х. Таким образом, если одна СВ в двумерной системе не зависит от другой СВ, то и вторая не зависит от первой. Это свойство называется взаимностью независимости случайных величин. От противного легко доказать взаимность зависимости случайных величин: если одна СВ в двумерной системе зависит от другой СВ, то и вторая зависит от первой. Заметим, что теперь нет смысла говорить «такая-то СВ зависит (не зависит) от такой-то», лучше говорить «такие-то величины зависимы (независимы)».

Пусть X, Y независимы, тогда f(x/y)=f_x(x), f(y/x)=f_y(y). Подставив первое равенство в (4.4.2), а второе - в (4.4.1), получим одно и то же:

f(x, y)=fx(x)fy(y) (X, Y - независимы).

(4.4.4)

Наоборот, подставив (4.4.4) в (4.4.1) или в (4.4.2), найдем, что X, Y независимы. В математике разбиение функции двух переменных на произведение двух функций одной переменной называется факторизацией. Т. о., мы доказали важный признак независимости случайных величин: для независимости двух случайных величин необходимо и достаточно факторизации их двумерной плотности вероятности.

Значение этого признака состоит в его простоте: мы не только просто устанавливаем, имеется ли независимость между СВ, но и, в случае, если она имеется, просто (минуя интегрирование) находим частные плотности. Следует, правда, иметь в виду, что факторизация неоднозначна с точностью до постоянного множителя; эта неоднозначность снимается, если хотя бы одна функция-множитель нормирована (тогда и другая автоматически нормирована); нормирование функции-множителя может потребовать интегрирования.

Примеры. 1. В двумерной системе с плотностью f(x, y)=

= случайные величины X, Y независимы, т. к. имеется факторизация: f(x, y)=f_x(x)f_y(y)=.

2. В двумерной системе с плотностью f(x, y)=exp[-(x²+y²)/2] случайные величины X, Y независимы, т. к. имеется факторизация:

f(x, y)=f_x(x)f_y(y)=.

3. В двумерной системе с плотностью f(x, y)=Aexp[-a(x²-bxy+y²)], где A>0, a>0, b0, случайные величины X, Y зависимы, т. к. факторизация невозможна.

Установленный признак независимости одновременно дает способ нахождения двумерной плотности по одномерным: как следует из (4.4.4), в случае независимости СВ двумерная плотность равна произведению частных плотностей (как уже подчеркивалось, в случае зависимости СВ двумерная плотность не может быть найдена только по частным плотностям; необходима дополнительная количественная информация о статистической зависимости этих СВ).

Установим три следствия признака независимости. Если случайные величины в двумерной системе независимы, то:

1. Двумерная функция распределения факторизуется:

F(x, y)=Fx(x)Fy(y), (X, Y - независимы).

(4.4.5)

Действительно, при независимости X, Y имеем:

F(x, y)=.

2. Все начальные и все центральные моменты факторизуются:

, (X, Y - независимы).

(4.4.6)

Действительно, при независимости X, Y имеем:

.

3. Двумерная характеристическая функция факторизуется:

, (X, Y - независимы)

(4.4.7)

Действительно, при независимости X, Y имеем:

В первом и третьем следствиях верно и обратное: если факторизуется двумерная функция распределения или двумерная характеристическая функция, то факторизуется двумерная плотность, а значит - СВ независимы. Во втором следствии обратное верно только если факторизуются моменты всех порядков: если моменты каких-то порядков не факторизуются, то СВ в системе зависимы. Из (4.4.6) в частности, вытекает, что

, если X, Y - независимы,

(4.4.7)

т. к. центральный момент первого порядка равен нулю. Этот важный результат понадобится ниже.

Поскольку совместная плотность вероятности несет всю информацию о системе случайных величин, то и условные плотности могут быть определены из двумерной плотности. Действительно, из (4.4.1) имеем:

f(y/x)=,

(4.4.8)

а из (4.4.2):

f(x/y)=.

(4.4.9)

Нужно иметь в виду, что в этих формулах х - в первой, и у - во второй, должны быть такими, при которых f_x(x)0 и f_y(y)0, соответственно.

До сих пор обсуждался лишь вопрос о наличии статистической зависимости, или ее отсутствии. Кратко обсудим вопрос о степени и о характере статистической зависимости. Полное описание того и другого дают условные плотности f(x/y), f(y/x) как функции двух переменных. Действительно, пусть X и Y зависимы; рассмотрев семейство условных плотностей f(x/y) величины Х при нескольких заданных значениях у, получаем исчерпывающую информацию о зависимости X от Y. Аналогично, рассмотрев семейство условных плотностей f(y/x) величины Y при нескольких заданных значениях х, получаем исчерпывающую информацию о зависимости Y от X. При этом характер статистической зависимости, к примеру, X от Y, проявляется в характере изменений в f(x/y) по мере изменения у; степень же зависимости Х от Y можно оценить возможным разбросом значений величины Х при заданном y: чем меньше этот разброс, тем выше степень зависимости (жестче зависимость). В пределе, когда при заданном Y=y разброс Х отсутствует, имеем детерминированную зависимость Х от Y; в другом пределе, когда f(x/y) вообще не зависит от у, зависимость X от Y отсутствует.

Придадим этим рассуждениям количественную форму. Введем условные моменты величины Х: начальный условный момент порядка k

,

и центральный условный момент порядка k

,

где m_X/y - условное математическое ожидание величины Х при заданном Y=y. Аналогично вводятся условные моменты величины Y: . Зависимость m_X/y от у называется регрессией Х на Y и, очевидно, отражает важнейшую черту характера зависимости X от Y, а именно, зависимость центра тяжести условного распределения Х от условия у. В той же мере зависимость m_Y/x от х, называемая регрессией Y на X, отражает зависимость центра тяжести условного распределения Y от условия х. Условная дисперсия величины Х D_X/y= дает возможность оценить степень зависимости Х от Y: чем меньше условное среднеквадратичное отклонение , тем жестче эта зависимость; в пределе при зависимость переходит в детерминированную вида X=, где - обычная функция. Аналогично, условное среднеквадратичное отклонение тем меньше, чем жестче зависимость Y от Х.

Таким образом, полную характеризацию зависимости между двумя случайными величинами дают два семейства условных плотностей, неполную, но существенную часть этой информации несут функциональные зависимости условных математических ожиданий и условных с. к. о. от условий. Недостатком этих описаний зависимости является их сложность.

4.4.2. Линейная статистическая зависимость (корреляция).

Поставим вопрос: нельзя ли описать зависимость между двумя СВ с помощью числа, наподобие того, как числами описываются асимметрия, эффективная ширина, эксцесс распределения? Ясно, что с помощью одного числа нельзя получить ни полного, ни даже приближенного описания характера (структуры) зависимости, но можно попытаться задать степень зависимости. Среди различных предложенных числовых мер степени статистической зависимости наибольшее применение, вследствие своего удобства и ясности интерпретации, нашла так называемая корреляционная мера, к рассмотрению которой сейчас переходим.

Вернемся ко второму смешанному центральному моменту системы (X, Y), кратко рассмотренному в п. 4.2:

.

Из различных названий и обозначений этой величины (см. п. 4.2) сейчас удобно выбрать название ковариация и обозначение K_X,Y . Как следует из (4.4.7), если X, Y независимы, K_X,Y=0. Обратное неверно: можно привести примеры двумерных систем, в которых X, Y зависимы, но K_X,Y=0. Можно заподозрить, что K_X,Y отражает не зависимость общего вида, а некоторый специальный вид статистической зависимости. Это так и есть: ковариация связана с частным видом статистической зависимости, называемой линейной статистической зависимостью.

Определение. Говорят, что между X и Y есть линейная статистическая зависимость (корреляция), если при a0, возможно однозначное представление

Y=aX+b+Z,

(4.4.10)

где a и b - вещественные неслучайные величины, Z - случайная величина, не зависящая от X, и a подобрано так, чтобы D_Z была минимальной. При этом прямая называется прямой регрессии. Если же такое представление возможно лишь при а=0, или возможно не одно такое представление с одинаковыми минимальными D_Z, то говорят, что между X и Y нет линейной статистической зависимости, но, может быть, есть статистическая зависимость другого вида.

Смысл линейной статистической зависимости легче всего понять в геометрической интерпретации. Рассмотрим случайный эксперимент, в котором регистрируются пары (х,у) значений случайных величин X и Y. Каждая пара изображается точкой на плоскости, в которой введена декартова система координат. Зарегистрировав достаточно много пар и нанеся соответствующие точки, получаем т. н. диаграмму разброса для системы (X, Y). Прямая, проведенная на диаграмме разброса так, чтобы сумма квадратов расстояний точек от нее была минимальной, называется прямой среднеквадратичной регрессии. Эта прямая - аналог прямой регрессии и отличается от нее в силу случайности положений точек на диаграмме разброса. С увеличением числа точек прямая среднеквадратичной регрессии стремится к прямой регрессии.

Примеры диаграмм разброса показаны на рис.4.4.1 - 4.4.4. На рис 4.4.1 приведена диаграмма разброса для системы (X, Y), в которой представление (4.4.10) возможно при некотором a>0; пунктиром показана прямая среднеквадратичной регрессии. В этом случае в системе (X, Y) имеется положительная линейная статистическая зависимость.

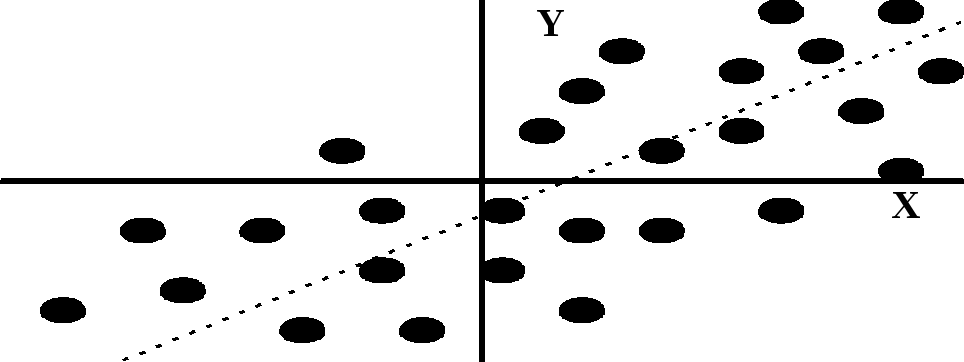
Рисунок 4.4.1. Рисунок 4.4.2.

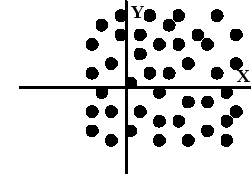
Рисунок 4.4.3. Рисунок 4.4.4.

На рис 4.4.2 приведена диаграмма разброса для системы (X, Y), в которой представление (4.4.10) возможно при некотором a<0; пунктиром показана прямая среднеквадратичной регрессии. В этом случае в системе (X, Y) имеется отрицательная линейная статистическая зависимость.

На рис. 4.4.3 приведена диаграмма разброса для системы (X, Y), имеющей равномерное распределение в прямоугольнике П: (a<x<b, c<y<d). Двумерная плотность вероятности этого распределения, как легко видеть, равна:

Частные плотности вероятности:

Условные плотности вероятности:

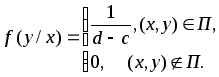
Как видим, в области, где , условные плотности не зависят от условий, т. е., по определению, между X и Y отсутствует статистическая зависимость, в том числе и линейная статистическая зависимость. Это подтверждается и тем, что в данном случае двумерная плотность факторизуется:

.

Диаграмма разброса подтверждает сделанный вывод об отсутствии линейной статистической зависимости: по диаграмме видно, что представление (4.4.10) при невозможно.

На рис. 4.4.4 приведена диаграмма разброса для системы (X, Y), имеющей равномерное распределение в круге

K:

радиуса R с центром в т. (x_c , y_c). Двумерная плотность вероятности этого распределения, как легко видеть, равна:

Записав уравнения верхней и нижней полуокружностей:

найдем частные плотности вероятности:

и, аналогично,

Условные плотности вероятности:

и, аналогично,

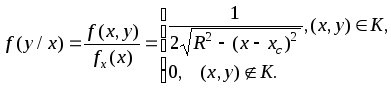
Как видим, условные плотности зависят от условий, следовательно, X и Y статистически зависимы. Это подтверждается и тем, что условные плотности - равномерные (в пределах, зависящих от условия), в то время как частные распределения не равномерны, и тем, что двумерная плотность не факторизуется. Замечательно, однако, что линейная статистическая зависимость между X и Y отсутствует (ниже это показано строго). Действительно, прямая среднеквадратичной регрессии на диаграмме разброса рис. 4.4.4 не единственна.

Подведем итоги рассмотрения диаграмм на рис. 4.4.1 - 4.4.4. Рис. 4.4.1 соответствует системе СВ с положительной корреляцией, рис. 4.4.2 - системе с отрицательной корреляцией, рис. 4.4.3 - системе, в которой отсутствует корреляция и зависимость вообще, рис. 4.4.4 - системе, в которой отсутствует корреляция, но не зависимость вообще (здесь имеется нелинейная статистическая зависимость).

Упростим и уточним терминологию. Синонимом выражения «линейная статистическая зависимость» является слово «корреляция». Если представление (4.4.10) возможно, единственно и а>0, то говорят, что имеется положительная корреляция (прямая регрессии имеет положительный наклон), если a<0 - отрицательная корреляция (прямая регрессии имеет отрицательный наклон). Если линейной статистической зависимости нет, говорят, что отсутствует корреляция между X и Y. Степень корреляции понимается как мера тесноты точек диаграммы вокруг прямой: расположение точек точно на прямой означает полную корреляцию, отсутствие линейной зависимости означает нулевую корреляцию, промежуточные случаи охватываются понятием частичная корреляция. Теперь можно сказать (пока на качественном уровне): если зависимости между X и Y нет, то нет и корреляции; если корреляции нет, то зависимость, может быть, есть, а может быть, ее нет.