Конспект лекций Глазова / 11.4. Примеры примен нер К-Р

11.4. Примеры применения неравенства Крамера-Рао.

Пример 1. Класс нормальных N(m, ) распределений с известным ; оцениваемый параметр - m, имеет смысл математического ожидания. Плотность вероятности одного выборочного значения

,

плотность вероятности простой выборки

.

Нетрудно проверить, что все условия регулярности выполнены. Логарифмическая функция правдоподобия

,

где С - выражение, не зависящее ни от выборочных значений, ни от параметра m, а поэтому даст нуль при последующем дифференцировании по m. Первая производная логарифмической функции правдоподобия

.

Как видим, в выражение входит достаточная статистика; обозначив ее как

,

получим

.

Вторая производная

,

и поскольку она не зависит от выборочных данных, ее математическое ожидание равно ей самой:

.

По формуле (11.3.4) находим фишеровскую информацию выборки

.

Неравенство Крамера-Рао для несмещенной оценки в данном случае имеет вид

.

Возьмем наугад какую-нибудь оценку для m и определим ее эффективность. Поскольку смысл оцениваемого параметра - математическое ожидание, разумно в качестве оценки попробовать выборочное среднее:

.

Найдя математическое ожидание этой оценки:

,

видим, что она несмещенная; найдя дисперсию этой оценки:

,

видим, что она достигает нижней грани неравенства Крамера-Рао (правая часть (11.4.1)), т. е. взятая оценка эффективна.

Для дальнейшего полезно заметить, что в данном примере имелась достаточная статистика S, что взятая оценка выражалась через выборочные значения только через S, и что связана с S линейно.

Пример 2. Класс нормальных N(m, ) распределений с известным m; оцениваемый параметр имеет смысл дисперсии. Плотность вероятности одного выборочного значения

,

логарифмическая функция правдоподобия одного выборочного значения

,

первая производная

,

вторая производная

,

среднее от нее

,

фишеровская информация одного выборочного значения

,

фишеровская информация выборки

,

неравенство Крамера-Рао для несмещенной оценки

.

Возьмем наугад какую-нибудь оценку для D_x и определим ее эффективность. Поскольку смысл оцениваемого параметра - дисперсия, разумно в качестве оценки попробовать выборочную дисперсию

.

Найдем среднее и дисперсию этой оценки:

,

т. е. оценка несмещенная;

.

Вычисляем первый член справа:

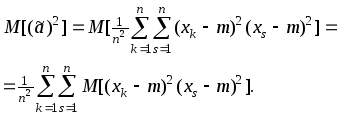
Найдя с учетом нормальности выборочных значений

и подставив в предыдущее равенство, получим:

.

Подставив этот результат в выражение для , получим:

.

Сравнивая с правой частью неравенства Крамера-Рао, видим, что оценка эффективная. И в этом случае можно найти, что имеется достаточная статистика

,

что взятая оценка выражалась через выборочные значения только через S, и что связана с S линейно.

Пример 3. Класс экспоненциальных распределений

;

оцениваемый параметр . В п. 3.8 было найдено, что для этого распределения m_x=1/, D_x=1/, следовательно параметр а имеет смысл математического ожидания (или с. к. о.). Логарифмическая функция правдоподобия одного выборочного значения

,

первая производная

,

вторая производная

,

среднее от нее

,

фишеровская информация одного выборочного значения

,

фишеровская информация выборки

,

неравенство Крамера-Рао для несмещенной оценки

.

Возьмем наугад какую-нибудь оценку для а и определим ее эффективность. Поскольку смысл оцениваемого параметра - математическое ожидание, разумно в качестве оценки попробовать выборочное среднее:

.

Математическое ожидание и дисперсия этой оценки были найдены в примере 1:

,

и поскольку в данном случае , имеем

.

Т. о. взятая оценка несмещенная и эффективная.

Пример 4. В предыдущих примерах «наугад» взятые оценки оказывались и несмещенными, и эффективными. Может возникнуть впечатление, что в большинстве случаев это так и есть, и что смещенные и неэффективные оценки бывают редко. Это впечатление неверно: само существование эффективной оценки в конкретной задаче оценивания, как будет показано далее, обеспечено в довольно узком классе распределений и параметров, поэтому эффективная оценка - это скорее исключение, чем правило. Чтобы продемонстрировать это, рассмотрим тот же класс распределений, что в предыдущем примере, но в качестве оцениваемого параметра возьмем . Поставим вопрос: если, как показано в предыдущем примере, найдена несмещенная эффективная оценка параметра , то не означает ли это, что в том же классе распределений существует эффективная оценка параметра ; если ответ положительный, то не будет ли оценка параметра обратной величиной оценки параметра а? Оказывается, что ответ на оба вопроса отрицательный: можно показать, что в классе экспоненциальных распределений эффективной оценки параметра не существует, т. е. правая часть соответствующего неравенства Крамера-Рао не достигается ни одной оценкой этого параметра.

Пример 5. Класс равномерных распределений

оцениваемый параметр . Математическое ожидание , откуда следует, что смысл оцениваемого параметра - удвоенное математическое ожидание. Логарифмическая функция правдоподобия одного выборочного значения

,

первая производная

,

фишеровская информация одного выборочного значения

,

фишеровская информация выборки

.

Одно из условий регулярности, а именно, условие 5, нарушено: область W значений Х, в которой f(x)>0, зависит от истинного значения параметра . Поэтому неравенство Крамера-Рао, которое в данном случае имеет вид

,

может не выполняться (поэтому, также, мы не использовали формулу (11.3.4)).

Возьмем наугад какую-нибудь оценку для а и определим ее эффективность. Поскольку смысл оцениваемого параметра - удвоенное математическое ожидание, разумно в качестве оценки попробовать удвоенное выборочное среднее:

.

Математическое ожидание этой оценки

,

т. е. оценка несмещенная. Дисперсия взятой оценки

,

и поскольку для равномерного распределения (см. п. 3.8)

,

то

.

Эта дисперсия меньше правой части предполагаемого неравенства Крамера-Рао, следовательно, по причине, указанной выше, это неравенство в данном случае несправедливо.

Случай дискретной генеральной СВ. До сих пор рассматривалось оценивание параметров распределений непрерывных генеральных СВ. Как показано в п. 11.3, неравенство Крамера-Рао в форме (11.3.1) справедливо и для случая дискретной генеральной СВ; там же приведены условия регулярности для этого случая. При выполнении этих условий, по-прежнему, , где I₁(a) - информация в одном выборочном значении, и по-прежнему справедлива формула (11.3.4). Изменится только выражение для I₁(a): в случае дискретной генеральной СВ

,

где - логарифмическая функция правдоподобия одного выборочного значения.

Пример 6. Класс биномиальных распределений

,

оцениваемый параметр р, параметр N известен. Поскольку математическое ожидание биномиального распределения (см. п. 3.7) m_x=Np, смысл оцениваемого параметра следует из соотношения p=m_x/N. Логарифмическая функция правдоподобия одного выборочного значения

,

первая производная

,

фишеровская информация одного выборочного значения

.

Сумма в правой части совпадает с выражением для дисперсии биномиального распределения, следовательно, она равна Np(1-p), в результате

,

фишеровская информация выборки

,

неравенство Крамера-Рао для несмещенной оценки

.

Возьмем наугад какую-нибудь оценку для р и определим ее эффективность. Имея в виду смысл оцениваемого параметра, разумно в качестве оценки попробовать

,

где - выборочные значения. Математическое ожидание оценки

,

т. е. оценка несмещенная. Дисперсия оценки

,

и сравнивая с правой частью неравенства Крамера-Рао, видим, что оценка эффективная. Заметим, что и в этом примере имелась достаточная статистика

,

что взятая оценка выражалась через выборочные значения только через S, и что связана с S линейно.

Пример 7. Класс распределений Пуассона

,

оцениваемый параметр , смысл оцениваемого параметра - математическое ожидание. Логарифмическая функция правдоподобия одного выборочного значения

,

первая производная

,

фишеровская информация одного выборочного значения

.

Сумма в правой части совпадает с выражением для дисперсии распределения Пуассона, следовательно, она равна , в результате

,

фишеровская информация выборки

,

неравенство Крамера-Рао для несмещенной оценки

.

Возьмем наугад какую-нибудь оценку для р и определим ее эффективность. Имея в виду смысл оцениваемого параметра, разумно в качестве оценки попробовать

.

Математическое ожидание оценки

,

т. е. оценка несмещенная. Дисперсия оценки

,

и сравнивая с правой частью неравенства Крамера-Рао, видим, что оценка эффективная. Заметим, что и в этом примере имелась достаточная статистика

,

что взятая оценка выражалась через выборочные значения только через S, и что связана с S линейно.